Attention机制全解

前言

之前已经提到过好几次Attention的应用，但还未对Attention机制进行系统的介绍，之后的实践模型attention将会用到很多，因此这里对attention机制做一个总结。

Seq2Seq

注意力机制（Attention Mechanism）首先是用于解决 Sequence to Sequence 问题提出的，因此我们了解下研究者是怎样设计出Attention机制的。

Seq2Seq，即序列到序列，指的是用Encoder-Decoder框架来实现的端到端的模型，最初用来实现英语-法语翻译。Encoder-Decoder框架是一种十分通用的模型框架，其抽象结构如下图所示：

其中，Encoder和Decoder具体使用什么模型都是由研究者自己定的，CNN/RNN/Transformer均可。Encoder的作用就是将输入序列映射成一个固定长度的上下文向量C，而Decoder则将上下文向量C作为预测\(Y_1\)输出的初始向量，之后将其作为背景向量，并结合上一个时间步的输出来对下一个时间步进行预测。

由于Encoder-Decoder模型在编码和解码阶段始终由一个不变的语义向量C来联系着，这也造成了如下一些问题：

• 所有的输入单词 X 对生成的所有目标单词 Y 的影响力是相同的
• 编码器要将整个序列的信息压缩进一个固定长度的向量中去，使得语义向量无法完全表示整个序列的信息
• 最开始输入的序列容易被后输入的序列给覆盖掉，会丢失许多细节信息，这点在长序列上表现的尤为明显

Attention机制的引入

Attention机制的作用就是为模型增添了注意力功能，使其倾向于根据需要来选择句子中更重要的部分。

加入加入Attention机制的Seq2Seq模型框架如下图所示：

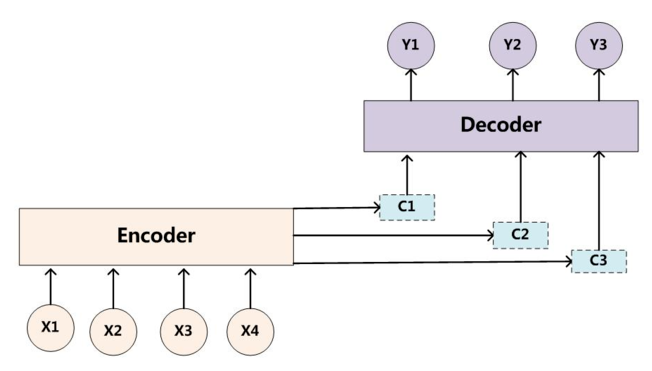
与传统的语义向量C不同的是，带有注意力机制的Seq2Seq模型与传统Seq2Seq模型的区别如下：

• 其为每一次预测都有不同的上下文信息\(C_i\)
  \[P(y_i|y_1, y_2, ..., y_{i-1}, X) = P(y_i-1, s_i, c_i)\]

其中\(s_i\)表示Decoder上一时刻的输出状态，\(c_i\)为当前的时刻的中间语义向量

• 当前的时刻的中间语义向量\(c_i\)为对输入信息注意力加权求和之后得到的向量，即：
  \[c_i = \sum_{j=1}^{Tx}\alpha_{ij}h_j\]

其中\(h_j\)为Encoder端的第j个词的隐向量，\(\alpha_{ij}\)表示Decoder端的第i个词对Encoder端的第j个词的注意力大小，即输入的第j个词对生成的第i个词的影响程度。这意味着在生成每个单词\(Y_i\)的时候，原先都是相同的中间语义表示\(C\)会替换成根据当前生成单词而不断变化的\(c_i\)。生成\(C_i\)最关键的部分就是注意力权重\(\alpha_{ij}\)的计算，具体的计算方法我们下面再讨论。

Hard or Soft

之前我们提到的为Soft Attention的一般形式，还有一种Hard Attention，其与Soft Attention的区别在于，其通过随机采样或最大采样的方式来选取特征信息（Soft Attention是通过甲醛求和的方式），这使得其无法使用反向传播算法进行训练。因此我们常用的通常是Soft Attention

Global or Local

Global Attention 与 Local Attention 的区别在于二者的关注范围不同。Global Attention 关注的是整个序列的输入信息，相对来说需要更大的计算量。而 Local Attention 仅仅关注限定窗口范围内的序列信息，但窗口的限定使得中心词容易忽视不在窗口范围内的信息，因此窗口的大小设定十分重要。在实践中，默认使用的是Global Attention。

注意力的计算

我们之前已经讨论过，中间语义向量\(c_i\)为对输入信息注意力加权求和之后得到的向量，即：
\[c_i = \sum_{j=1}^{Tx}\alpha_{ij}h_j\]

而注意力权重\(\alpha_{ij}\)表示Decoder端的第i个词对Encoder端的第j个词的注意力大小，即输入的第j个词对生成的第i个词的影响程度。其基本的计算方式如下：
\[\alpha_{ij} = \frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})}\]

\[e_{ij} = Score(s_{i-1}, h_j)\]

其中，\(s_{i-1}\)需要根据具体任务进行选择，对于机器翻译等生成任务，可以选取 Decoder 上一个时刻的隐藏层输出，对于阅读理解等问答任务，可以选择问题或问题+选项的表征，对于文本分类任务，可以是自行初始化的上下文向量。而\(h_j\)为 Encoder 端第j个词的隐向量，分析上面公式，可以将Attention的计算过程总结为3个步骤：

• 将上一时刻Decoder的输出与当前时刻Encoder的隐藏词表征进行评分，来获得目标单词 Yi 和每个输入单词对应的对齐可能性（即一个对齐模型），Score(·)为一个评分函数，一般可以总结为两类：
  • 点积/放缩点积：
    \[e_{ij} = Score(s_{i-1}, h_j) = s_{i-1} \cdot h_j\]

  \[e_{ij} = Score(s_{i-1}, h_j) = \frac{s_{i-1} \cdot h_j}{||s_{i-1}||\cdot||h_j||}\]

  • MLP网络：
    \[e_{ij} = Score(s_{i-1}, h_j) = MLP(s_{i-1}, h_j)\]

  \[e_{ij} = Score(s_{i-1}, h_j) = s_{i-1}Wh_{j}\]

  \[e_{ij} = Score(s_{i-1}, h_j) = W|h_j;s_{i-1}|\]

• 得到对齐分数之后，用Softmx函数将其进行归一化，得到注意力权重

• 最后将注意力权重与 Encoder 的输出进行加权求和，得到需要的中间语义向量\(c_i\)

将公式整合一下：
\[c_{i,j} = Attention(Query, Keys, Values) = Softmax(Score(Query, Keys)) * Values\]

其中，\(Query\)为我们之前提到的\(s_{i-1}\)，\(Keys\) 和 \(Values\)为 \(h\)

Self-Attention

重温一下我们讲解Transformer时提到的Self-Attention，其 \(Query\)，\(Keys\) 和 \(Values\) 均为词表征通过一个简单的线性映射矩阵得到的，即可将其表示为
\[Attention(Q,K,V) = Attention(W^QX,W^KX,W^VX)\]

从其注意力分数的计算方法上来看也是一种典型的缩放点积，其关键在于仅对句子本身进行注意力权值计算，使其更能够把握句子中词与词之前的关系，从而提取出句子中的句法特征或语义特征。

小结

这一块对Attention的原理基本已经全部总结了，主要是对自己只是的巩固，以及对之后的实践工作做铺垫，之后有时间再将Attention这块相关的代码写出来。

参考链接
https://zhuanlan.zhihu.com/p/31547842
https://zhuanlan.zhihu.com/p/59698165
https://zhuanlan.zhihu.com/p/53682800
https://zhuanlan.zhihu.com/p/43493999