一元线性回归与R语言

（https://mirrors.tuna.tsinghua.edu.cn/CRAN/）下载好R之后打开，就可以输入命令，如下，我输入

> y=c(61,57,58,40,90,35,68) 　　表示创建一个y向量，向量的值是c后面的内容
> y　　回显y
[1] 61 57 58 40 90 35 68　　
> x=c(170,168,175,153,185,135,172)　　创建一个x向量

> x　　回显x
[1] 170 168 175 153 185 135 172
>
> plot(x,y)　　以x做横坐标，y做左纵坐标，画散点图
> z=lm(y~x+1)　　　　以一元函数(y=ax+b)的形式做线性回归模型

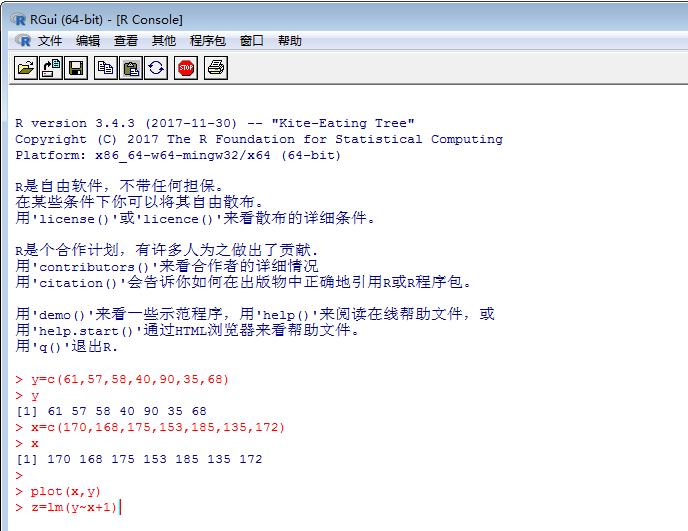
然后，输入summary(z)就求解了，结果如下图

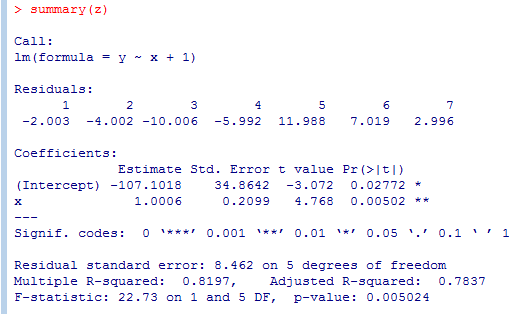
我们是一元线性建模，所以最后得到的应该是y=ax+b这样的东东，所以主要是求a和b的值。

下面我解释一下上面的回显

1.

"Estimate" ，就是那个1.0006，就表示a的值，-107.1018表示b的值，也就是一元函数的截距的值

2.

Residuals:
1 2 3 4 5 6 7
-2.003 -4.002 -10.006 -5.992 11.988 7.019 2.996

这个是列出了各项残差，所谓残差，就是每个点到拟合直线的“距离”，之所以打了引号，是因为确实不是直线距离，而是点到直线的，平行于轴的线段的长度，之所以没有取垂直距离，是因为计算方面的简便，具体我记不住

3.

Residual standard error: 残差的标准差，什么是标准差呢

4.Multiple R-squared ，定义为样本相关系数的平方，我不懂，但已知薛毅书纸介质p270页有R平方的定义，见 6.3.3 显著性检验