图论分支-Tarjan初步-边双联通分量

本来应该先说强连通分量，但是有一定的分配，所以这个在下一篇博客将会见到。

这个本想连点连通分量一起讲，但是量有点大，所以我就分两步讲。

我们先看定义

再来看看图解

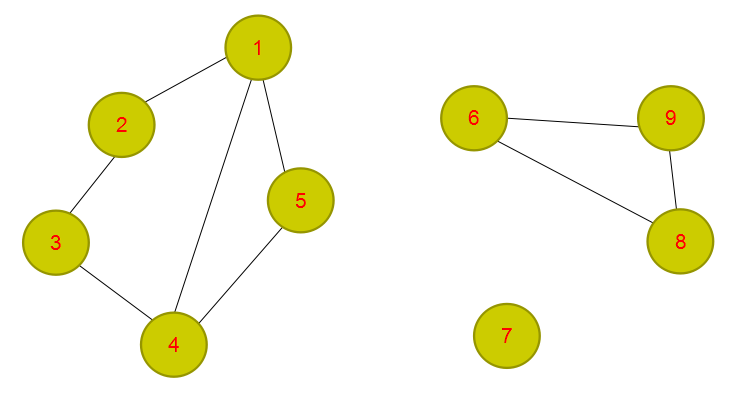
很容易就能发现，只要将割边断掉，然后剩下的连通块就是我们的边双，那么我们的代码就可以yy出来了，先跑一遍Tarjan求割点，然后在去跑dfs，将每一个边双染色，那么就可以了,而染色操作，以便于我们后面好缩点。

我们来看模板

void Tarjan(int x,int fa){
    low[x]=dfn[x]=++t;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!dfn[y]){
            Tarjan(y,i);
            low[x]=min(low[y],low[x]);
            if(low[y]>dfn[x])
                edge[i].flag=edge[(i^)].flag=;//寻找割边 ，并标记
        }else if((i^)!=fa){
            low[x]=min(low[x],dfn[y]);
        }
    }
}

void dfs(int x){
    col[x]=tot;//染色
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!col[y]&&!edge[i].flag)//不能是走过的点和割边
            dfs(y);//遍历
    }
}

//下面插入主函数中

for(int i=;i<=n;i++){
        if(!dfn[i]) Tarjan(i,-);
    }
for(int i=;i<=n;i++){
    if(!col[i]) ++tot,dfs(i);
}

大家仔细琢磨一下，应该就能懂他的思想了。

然后我们来看例题：

这道题很显然是将这个图变为边双。在同一个边双连通分量中，任意两点都有至少两条独立路可达，所以同一个边双连通分量里的所有点可以看做同一个点。 这时就要用到我们的染色缩点，缩点请仔细思考怎么做。

缩点后，新图是一棵树，树的边就是原无向图的桥。 现在问题转化为：在树中至少添加多少条边能使图变为双连通图。

此时我们就能想出之前我们学过的入度和出度；

那么，只要将度为一的点连边即可，那么此时我们的公式就是添加边数=（树中度为1的节点数+1）/2；

具体做法就是：

首先把两个最近公共祖先最远的两个叶节点之间连接一条边，这样可以把这两个点到祖先的路径上所有点收缩到一起，因为一个形成的环一定是双连通的。 然后再找两个最近公共祖先最远的两个叶节点，这样一对一对找完，恰好是(leaf+1)/2次，把所有点收缩到了一起。

这样就解决了，来看

Code

#include<bits/stdc++.h>
#define maxn 5007
#define M 20007
using namespace std;
int n,m,t,head[maxn],cent=,low[maxn],dfn[maxn],vis[maxn];
int tot,col[maxn],out[maxn],ans,in[maxn],ol;
struct node{
    int next,to,flag,from;
}edge[M<<];

void add(int u,int v){
    edge[++cent]=(node){head[u],v,,u};head[u]=cent;
}

void Tarjan(int x,int fa){
    low[x]=dfn[x]=++t;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!dfn[y]){
            Tarjan(y,i);
            low[x]=min(low[y],low[x]);
            if(low[y]>dfn[x])
                edge[i].flag=edge[(i^)].flag=;//寻找割边 ，并标记
        }else if((i^)!=fa){
            low[x]=min(low[x],dfn[y]);
        }
    }
}

void dfs(int x){
    col[x]=tot;//染色
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!col[y]&&!edge[i].flag)//不能是走过的点和割边
            dfs(y);//遍历
    }
}

void make_dfs(int x,int fa){
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(y==fa) continue;
        out[y]++,in[x]++;//计算入度出度
        make_dfs(y,x);
    }
}

int main(){
//    freopen("rpaths.in","r",stdin);
//    freopen("rpaths.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=,a,b;i<=m;i++){
        scanf("%d%d",&a,&b);
        if(a==b) continue;
        add(a,b),add(b,a);
    }
    for(int i=;i<=n;i++){
        if(!dfn[i]) Tarjan(i,-);
    }
    for(int i=;i<=n;i++){
        if(!col[i]) ++tot,dfs(i);
    }
    memset(head,,sizeof(head));cent=;//预处理
    for(int i=;i<=*m+;i++){
        if(edge[i].flag){
            add(col[edge[i].from],col[edge[i].to]);
        }//重点！！！染色缩点建树
    }
    make_dfs(,-);//寻找度
    for(int i=;i<=tot;++i){
        if((out[i]==&&in[i]==)||(in[i]==&&!out[i])){
            ans++;//统计度为一的点
        }
    }
    printf("%d\n",(ans+)/);
}

下一道也很简单：

我们只要缩点，然后求距离就可以了，LCA求距离都懂的吧？（好像又没讲，下次下次）；

我的错，没说LCA，在讲完LCA后再来看这道吧，但看完后就懂代码了：

Code

#include<bits/stdc++.h>
#define maxn 100007
using namespace std;
int n,m,cent=,head[maxn],low[maxn],dfn[maxn],col[maxn],t,fa[maxn][];
int tot,dep[maxn],q;
struct node{
    int next,to,from,flag;
}edge[maxn<<];

void add(int u,int v){
    edge[++cent]=(node){head[u],v,u,};head[u]=cent;
}

void make_dfs(int x,int dy){
    dep[x]=dy;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(fa[x][]==y) continue;
        fa[y][]=x;
        make_dfs(y,dy+);
    }
}

void Init(){
    fa[][]=-;
    make_dfs(,);
    for(int i=;i<=;i++){
        for(int j=;j<=tot;j++){
            if(fa[j][i-]<) fa[j][i]=-;
            else fa[j][i]=fa[fa[j][i-]][i-];
        }
    }
    return ;
}

int lca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=,d=dep[x]-dep[y];d;d>>=,i++){
        if(d&) x=fa[x][i];
    }
    if(x==y) return x;
    for(int i=;i>=;i--){
        if(fa[x][i]!=fa[y][i]){
            x=fa[x][i];
            y=fa[y][i];
        }
    }
    return fa[x][];
}

void Tarjan(int x,int f){
    low[x]=dfn[x]=++t;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!dfn[y]){
            Tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if(low[y]>dfn[x])
                edge[i].flag=edge[(i^)].flag=;
        }else if((i^)!=f){
            low[x]=min(low[x],dfn[y]);
        }
    }
}

void dfs(int x){
    col[x]=tot;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!col[y]&&!edge[i].flag)
            dfs(y);
    }
}

int main(){
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=,a,b;i<=m;i++){
        scanf("%d%d",&a,&b);
        add(a,b),add(b,a);
    }
    for(int i=;i<=n;i++){
        if(!dfn[i]) Tarjan(i,-);
    }
    for(int i=;i<=n;i++){
        if(!col[i]) ++tot,dfs(i);
    }
    memset(head,,sizeof(head));cent=;
    for(int i=;i<=*m+;i++){
        if(edge[i].flag){
            add(col[edge[i].from],col[edge[i].to]);
        }//缩点套路，一定要会
    }
    Init();//LCA初始化
    scanf("%d",&q);
    for(int i=,a,b;i<=q;i++){
        scanf("%d%d",&a,&b);
        printf("%d\n",dep[col[a]]+dep[col[b]]-*dep[lca(col[a],col[b])]);//求距离
    }
}

这就差不多结束了，自己可以在找些题，要

深刻理解缩点的重要性