[转]类不平衡问题与SMOTE过采样算法

在前段时间做本科毕业设计的时候，遇到了各个类别的样本量分布不均的问题——某些类别的样本数量极多，而有些类别的样本数量极少，也就是所谓的类不平衡（class-imbalance）问题。

本篇简述了以下内容：

什么是类不平衡问题

为什么类不平衡是不好的

几种解决方案

SMOTE过采样算法

进一步阅读

什么是类不平衡问题

类不平衡（class-imbalance）是指在训练分类器中所使用的训练集的类别分布不均。比如说一个二分类问题，1000个训练样本，比较理想的情况是正类、负类样本的数量相差不多；而如果正类样本有995个、负类样本仅5个，就意味着存在类不平衡。

在后文中，把样本数量过少的类别称为“少数类”。

但实际上，数据集上的类不平衡到底有没有达到需要特殊处理的程度，还要看不处理时训练出来的模型在验证集上的效果。有些时候是没必要处理的。

为什么类不平衡是不好的

从模型的训练过程来看

从训练模型的角度来说，如果某类的样本数量很少，那么这个类别所提供的“信息”就太少。

使用经验风险（模型在训练集上的平均损失）最小化作为模型的学习准则。设损失函数为0-1 loss（这是一种典型的均等代价的损失函数），那么优化目标就等价于错误率最小化（也就是accuracy最大化）。考虑极端情况：1000个训练样本中，正类样本999个，负类样本1个。训练过程中在某次迭代结束后，模型把所有的样本都分为正类，虽然分错了这个负类，但是所带来的损失实在微不足道，accuracy已经是99.9%，于是满足停机条件或者达到最大迭代次数之后自然没必要再优化下去，ok，到此为止，训练结束！于是这个模型……

模型没有学习到如何去判别出少数类。

从模型的预测过程来看

考虑二项Logistic回归模型。输入一个样本 xx ，模型输出的是其属于正类的概率 ŷ y^ 。当 ŷ >0.5y^>0.5 时，模型判定该样本属于正类，否则就是属于反类。

为什么是0.5呢？可以认为模型是出于最大后验概率决策的角度考虑的，选择了0.5意味着当模型估计的样本属于正类的后验概率要大于样本属于负类的后验概率时就将样本判为正类。但实际上，这个后验概率的估计值是否准确呢？

从几率（odds）的角度考虑：几率表达的是样本属于正类的可能性与属于负类的可能性的比值。模型对于样本的预测几率为 ŷ 1−ŷ y^1−y^ 。

模型在做出决策时，当然希望能够遵循真实样本总体的正负类样本分布：设 θθ 等于正类样本数除以全部样本数，那么样本的真实几率为 θ1−θθ1−θ 。当观测几率大于真实几率时，也就是 ŷ >θy^>θ 时，那么就判定这个样本属于正类。

虽然我们无法获悉真实样本总体，但之于训练集，存在这样一个假设：训练集是真实样本总体的无偏采样。正是因为这个假设，所以认为训练集的观测几率 θ̂ 1−θ̂ θ^1−θ^ 就代表了真实几率 θ1−θθ1−θ 。

所以，在这个假设下，当一个样本的预测几率大于观测几率时，就应该将样本判断为正类。

几种解决方案

目前主要有三种办法：

1. 调整 θθ 值

根据训练集的正负样本比例，调整 θθ 值。   

这样做的依据是上面所述的对训练集的假设。但在给定任务中，这个假设是否成立，还有待讨论。

2. 过采样

对训练集里面样本数量较少的类别（少数类）进行过采样，合成新的样本来缓解类不平衡。

下面将介绍一种经典的过采样算法：SMOTE。

3. 欠采样

对训练集里面样本数量较多的类别（多数类）进行欠采样，抛弃一些样本来缓解类不平衡。

SMOTE过采样算法

  JAIR'2002的文章《SMOTE: Synthetic Minority Over-sampling Technique》提出了一种过采样算法SMOTE。概括来说，本算法基于“插值”来为少数类合成新的样本。下面介绍如何合成新的样本。

设训练集的一个少数类的样本数为 TT ，那么SMOTE算法将为这个少数类合成 NTNT 个新样本。这里要求 NN 必须是正整数，如果给定的 N<1N<1 那么算法将“认为”少数类的样本数 T=NTT=NT ，并将强制 N=1N=1 。

考虑该少数类的一个样本 ii ，其特征向量为 xi,i∈{1,...,T}xi,i∈{1,...,T} ：

1. 首先从该少数类的全部 TT 个样本中找到样本 xixi 的 kk 个近邻（例如用欧氏距离），记为 xi(near),near∈{1,...,k}xi(near),near∈{1,...,k} ；

2. 然后从这 kk 个近邻中随机选择一个样本 xi(nn)xi(nn) ，再生成一个 00 到 11 之间的随机数 ζ1ζ1 ，从而合成一个新样本 xi1xi1 ：

xi1=xi+ζ1⋅(xi(nn)−xi)xi1=xi+ζ1⋅(xi(nn)−xi)

3. 将步骤2重复进行 NN 次，从而可以合成 NN 个新样本：xinew,new∈1,...,Nxinew,new∈1,...,N。

那么，对全部的 TT 个少数类样本进行上述操作，便可为该少数类合成 NTNT 个新样本。

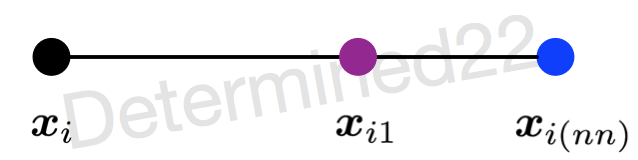
如果样本的特征维数是 22 维，那么每个样本都可以用二维平面上的一个点来表示。SMOTE算法所合成出的一个新样本 xi1xi1 相当于是表示样本 xixi 的点和表示样本 xi(nn)xi(nn) 的点之间所连线段上的一个点。所以说该算法是基于“插值”来合成新样本。

进一步阅读

有两篇翻译自国外博客的文章：

解决真实世界问题：如何在不平衡类上使用机器学习？

从重采样到数据合成：如何处理机器学习中的不平衡分类问题？

可以先读中文的了解一下说了哪些事情，如果感兴趣的话就去看英文原文来深入学习。

追加内容：

发现在实践中大部分时候还是欠抽样效果最好，SMOTE效果太差，制造的样本甚至会极大的影响样本的分布。

原文链接：https://www.cnblogs.com/Determined22/p/5772538.html