【模式匹配】Aho-Corasick自动机

1. 多模匹配

AC自动机（Aho-Corasick Automaton）是多模匹配算法的一种。所谓多模匹配，是指在字符串匹配中，模式串有多个。前面所介绍的KMP、BM为单模匹配，即模式串只有一个。假设主串\(T[1 \cdots m]\)，模式串有k个\(\mathbb{P} = \{ P_1, \cdots, P_k\}\)，且模式串集合的总长度为\(n\)。如果采用KMP来匹配多模式串，则算法复杂度为：

\[O(|P_1|+m+\cdots + |P_k|+m)=O(n+km)
\]

而KMP并没有利用到模式串之间的重复字符结构信息，每一次的匹配都需要将主串从头至尾扫描一遍。贝尔实验室的Aho与Corasick于1975年基于有限状态机（finite state machines）提出AC自动机算法[1]。小插曲：实际上AC算法比KMP提出要早，KMP是1977年才被提出来了的。

2. AC算法

AC自动机

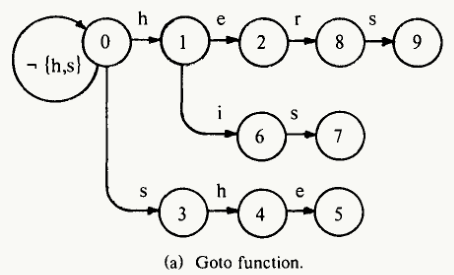
自动机由状态（数字标记的圆圈）和转换（带标签的箭头）组成，每一次转换对应一个字符。AC算法的核心包括三个函数：goto、failure、output；这三个函数构成了AC自动机。对于模式串{he, his, hers, she}，goto函数表示字符按模式串的转移，暗含了模式串的共同前缀的字符结构信息，如下图：

failure函数表示匹配失败时退回的状态：

output函数表示模式串对应于自动机的状态：

完整的AC自动机如下：

匹配

AC算法根据自动机匹配模式串，过程比较简单：从主串的首字符、自动机的初始状态0开始，

• 若字符匹配成功，则按自动机的goto函数转移到下一状态；且若转移的状态对应有output函数，则输出已匹配上的模式串；
• 若字符匹配失败，则递归地按自动机的failure函数进行转移

匹配母串的算法如下：

构造

AC自动机的确简单高效，但是如何构造其对应的goto、failure、output函数呢？首先来看goto函数，细心一点我们发现goto函数本质上就是一棵带有回退指针的trie树，利用模式串的共同前缀信息，与output函数共同表示模式串的字符结构的信息。

failure函数是整个AC算法的精妙之处，用于匹配失败时的回溯；且回溯到的状态\(state\)应满足：状态\(state\)能按当前状态的转移字符进行能goto到的状态，且能构成最长匹配。记\(g(r,a)=s\)表示状态r可以按字符a goto到状态s，则称状态r为状态s的前一状态，字符a为状态s的转移字符。failure函数满足这样一个规律：当匹配失败时，回溯到的状态为前一状态的failure函数值（我们称之为failure转移状态）按转移字符能goto到的状态；若不能，则为前一状态的failure转移状态的failure转移状态按转移能goto到的状态；若不能，则为......上面的话听着有点拗口，让我们以上图AC自动机为例子来说明：

• 对于状态7，前一状态6的failure转移状态为0，状态0按转移字符s可以goto到状态3，所以状态7的failure函数\(f(7)=3\)；
• 对于状态2，前一状态1的failure转移状态为0，状态0按转移字符e可以goto到状态0，所以状态2的failure函数\(f(2)=0\)；

其中，所有root节点（状态0）能goto到的状态，其failure函数值均为0。根据goto表（trie树）的特性，可知某一状态的前一状态、转移字符是唯一确定的。因此定义\(\beta(s)=r\)表示状态\(s\)的前一状态为\(r\)，\(\tau(s)=a\)指状态\(s\)的转移字符为\(a\)；记\(f^{i}(s)=f\left( f^{(i-1)}(s)\right)\)。那么，状态s的failure函数的计算公式为：

\[f(s) = \left\{ {\matrix{
{g\left( f^{n}(\beta(s)), \tau(s) \right)} & n = \arg \underset{i}{\min} \, \left\{ g\left( f^{i}(\beta(s)), \tau(s) \right) \neq failure \right\}\cr
{0} & else \cr
} } \right.
\]

在计算failure函数时，巧妙地运用队列进行递归构造，具体实现如下：

3. 实现

Talk is cheap, show me the code. Java版实现在这里；下面给出python实现（代码参考了 Implementation of the Aho-Corasick algorithm in Python）：

# coding=utf-8
from collections import deque, namedtuple

automaton = []
# state_id: int, value: char, goto: dict, failure: int, output: set
Node = namedtuple("Node", "state value goto failure output")

def init_trie(words):
    """
    creates an AC automaton, firstly create an empty trie, then add words to the trie
    and sets fail transitions
    """
    create_empty_trie()
    map(add_word, words)
    set_fail_transitions()

def create_empty_trie():
    """ initialize the root of the trie """
    automaton.append(Node(0, '', {}, 0, set()))

def add_word(word):
    """add word into trie"""
    node = automaton[0]
    for char in word:
        # char is not in trie
        if goto_state(node, char) is None:
            next_state = len(automaton)
            node.goto[char] = next_state  # modify goto(state, char)
            automaton.append(Node(next_state, char, {}, 0, set()))
            node = automaton[next_state]
        else:
            node = automaton[goto_state(node, char)]
    node.output.add(word)

def goto_state(node, char):
    """goto function"""
    if char in node.goto:
        return node.goto[char]
    else:
        return None

def set_fail_transitions():
    """construction of failure function, and update the output function"""
    queue = deque()
    # initialization
    for char in automaton[0].goto:
        s = automaton[0].goto[char]
        queue.append(s)
        automaton[s] = automaton[s]._replace(failure=0)
    while queue:
        r = queue.popleft()
        node = automaton[r]
        for a in node.goto:
            s = node.goto[a]
            queue.append(s)
            state = node.failure
            # failure transition recursively
            while goto_state(automaton[state], a) is None and state != 0:
                state = automaton[state].failure
            # except the chars in goto function, all chars transition will goto root node self
            if state == 0 and goto_state(automaton[state], a) is None:
                goto_a = 0
            else:
                goto_a = automaton[state].goto[a]
            automaton[s] = automaton[s]._replace(failure=goto_a)
            fs = automaton[s].failure
            automaton[s].output.update(automaton[fs].output)

def search_result(strings):
    """AC pattern matching machine"""
    result_set = set()
    node = automaton[0]
    for char in strings:
        while goto_state(node, char) is None and node.state != 0:
            node = automaton[node.failure]
        if node.state == 0 and goto_state(node, char) is None:
            node = automaton[0]
        else:
            node = automaton[goto_state(node, char)]
        if len(node.output) >= 1:
            result_set.update(node.output)
    return result_set

init_trie(['he', 'she', 'his', 'hers'])
print search_result("ushersm")

-------------------------------------------------------- 2016-06-14 更新 --------------------------------------------------------

实现了一个scala版本，支持添加词属性，代码托管在scala-AC。

4. 参考资料

[1] Aho, Alfred V., and Margaret J. Corasick. "Efficient string matching: an aid to bibliographic search." Communications of the ACM 18.6 (1975): 333-340.

[2] Pekka Kilpeläinen, Lecture 4: Set Matching and Aho-Corasick Algorithm.