hough变换是如何检测出直线和圆的？

（I）直线篇

1 直线是如何表示的？
对于平面中的一条直线，在笛卡尔坐标系中，常见的有点斜式，两点式两种表示方法。然而在hough变换中，考虑的是另外一种表示方式：使用（r,theta）来表示一条直线。其中r为该直线到原点的距离，theta为该直线的垂线与x轴的夹角。如下图所示。

2 如果坐标系中有多个点，又怎样识别出哪些点在一条直线上呢？
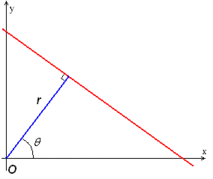
使用hough变换来检测直线的思想就是：为每一个点假设n个方向的直线，通常n=180，此时检测的直线的角度精度为1°，分别计算这n条直线的（r,theta）坐标，得到n个坐标点。如果要判断的点共有N个，最终得到的（r,theta）坐标有N*n个。有关这N*n个（r,theta）坐标，其中theta是离散的角度，共有180个取值。
最重要的地方来了，如果多个点在一条直线上，那么必有这多个点在theta=某个值theta_i时，这多个点的r近似相等于r_i。也就是说这多个点都在直线（r_i,theta_i）上。
3 下面拿个例子说明： 

如果空间中有3个点，如何判断这三个点在不在一个直线上，如果在，这条直线是的位置为？

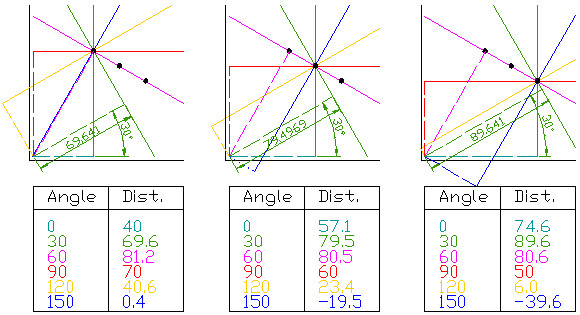
这个例子中，对于每个点均求过该点的6条直线的（r,theta）坐标，共求了3*6个（r,theta）坐标。可以发现在theta=60时，三个点的r都近似为80.7，由此可判定这三个点都在直线（80.7，60）上。
通过 r0theta 坐标系可以更直观表示这种关系，如下图：图中三个点的（r,theta）曲线汇集在一起，该交点就是同时经过这三个点的直线。

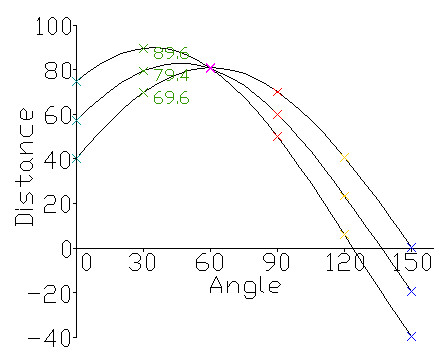
在实际的直线检测情况中，如果超过一定数目的点拥有相同的（r,theta）坐标，那么就可以判定此处有一条直线。在r0theta 坐标系图中，明显的交汇点就标示一条检测出的直线。
如下图，可以判定出平面上的点共构成了两条直线，即检测出两条直线。

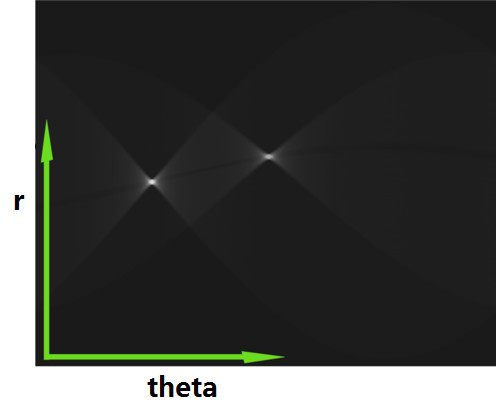
4 代码：

在matlab中提供了hough变换的代码，有hough，houghlines，houghpeaks，具体的使用可以在help中查到。

（II）圆篇

继使用hough变换检测出直线之后，顺着坐标变换的思路，提出了一种检测圆的方法。
1 如何表示一个圆？
与使用（r,theta）来表示一条直线相似，使用（a,b,r）来确定一个圆心为（a,b）半径为 r  的圆。
2 如何表示过某个点的所有圆？
某个圆过点（x1,y1），则有：(x1-a1)^2 + (y1-b1)^2 = r1^2 。
那么过点（x1,y1）的所有圆可以表示为（a1(i),b1(i),r1(i)），其中r1∈（0，无穷），每一个 i 值都对应一个不同的圆，（a1(i),b1(i),r1(i)）表示了无穷多个过点（x1,y1）的圆。
3 如何确定多个点在同一个圆上？
如(2)中说明，过点（x1,y1）的所有圆可以表示为（a1(i),b1(i),r1(i)），过点（x2,y2）的所有圆可以表示为（a2(i),b2(i),r2(i)），过点（x3,y3）的所有圆可以表示为（a3(i),b3(i),r3(i)），如果这三个点在同一个圆上，那么存在一个值（a0,b0,r0），使得 a0 = a1(k)=a2(k)=a3(k) 且b0 = b1(k)=b2(k)=b3(k) 且r0 =  r1(k)=r2(k)=r3(k)，即这三个点同时在圆（a0,b0,r0)上。
从下图可以形象的看出：

首先，分析过点（x1,y1）的所有圆（a1(i),b1(i),r1(i)），当确定r1(i)时 ，（a1(i),b1(i)）的轨迹是一个以（x1,y1,r1(i)）为中心半径为r1(i)的圆。那么，所有圆（a1(i),b1(i),r1(i)）的组成了一个以（x1,y1,0）为顶点，锥角为90度的圆锥面。
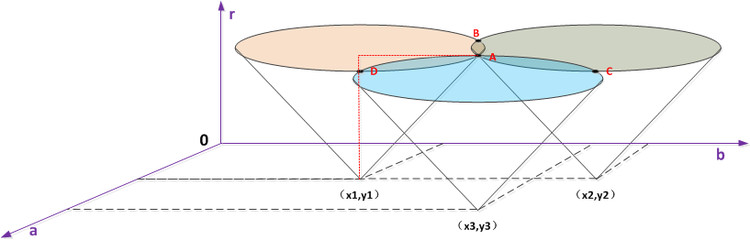
三个圆锥面的交点A 既是同时过这三个点的圆。
4 怎样用代码实现检测圆的过程？
 上面的分析虽然很简单，但是用代码实现起来就麻烦了，首先过每一个点的（a(i),b(i),r(i)）都有无穷多个，若是要检测的点很多，要两两比较所有的（a,b,r）值是否相等实在是一个巨大的运算量。
……未完待续……

 

转自：http://blog.163.com/yuyang_tech/blog/static/21605008320130233343990/