BZOJ 4305: 数列的GCD( 数论 )

对于d, 记{ai}中是d的倍数的数的个数为c, 那么有：

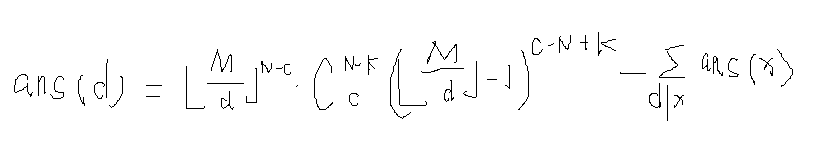
直接计算即可，复杂度O(NlogN+MlogM)

---------------------------------------------------------------------------

#include<cstdio>

#include<cstring>

#include<algorithm>

 

using namespace std;

 

typedef long long ll;

 

const int MOD = 1000000007;

const int maxn = 300009;

 

int ans[maxn];

int N, M, K, seq[maxn], cnt[maxn];

int Inv[maxn], Fac[maxn];

 

void gcd(int a, int b, int &d, int &x, int &y) {

if(!b) {

d = a;

x = 1;

y = 0;

} else {

gcd(b, a % b, d, y, x);

y -= x * (a / b);

}

}

 

int INV(int v) {

int d, x, y;

gcd(v, MOD, d, x, y);

return (x + MOD) % MOD;

}

 

void Init() {

Inv[0] = INV(Fac[0] = 1);

for(int i = 1; i <= N; i++) {

Fac[i] = ll(i) * Fac[i - 1] % MOD;

Inv[i] = INV(Fac[i]);

}

}

 

int C(int m, int n) {

return ll(Fac[n]) * Inv[n - m] % MOD * Inv[m] % MOD;

}

 

int Power(int x, int t) {

int ret = 1;

for(; t; t >>= 1, x = ll(x) * x % MOD)

if(t & 1) ret = ll(x) * ret % MOD;

return ret;

}

 

int main() {

memset(cnt, 0, sizeof cnt);

scanf("%d%d%d", &N, &M, &K);

for(int i = 0; i < N; i++) {

scanf("%d", seq + i);

cnt[seq[i]]++;

}

Init();

for(int i = M; i; i--) {

int c = 0;

for(int j = i; j <= M; j += i)

if(cnt[j]) c += cnt[j];

if(c + K < N) {

ans[i] = 0; continue;

}

ans[i] = (ll) Power(M / i, N - c) * C(N - K, c) % MOD * Power(M / i - 1, c - N + K) % MOD;

for(int j = i << 1; j <= M; j += i)

if((ans[i] -= ans[j]) < 0) ans[i] += MOD;

}

printf("%d", ans[1]);

for(int i = 2; i <= M; i++)

printf(" %d", ans[i]);

return 0;

}

---------------------------------------------------------------------------

4305: 数列的GCD

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 149  Solved: 68
[Submit][Status][Discuss]

Description

给出一个长度为N的数列{a[n]}，1<=a[i]<=M(1<=i<=N)。 

现在问题是，对于1到M的每个整数d，有多少个不同的数列b[1], b[2], ..., b[N]，满足： 

(1)1<=b[i]<=M(1<=i<=N)； 

(2)gcd(b[1], b[2], ..., b[N])=d； 

(3)恰好有K个位置i使得a[i]<>b[i](1<=i<=N) 

注：gcd(x1,x2,...,xn)为x1, x2, ..., xn的最大公约数。 

输出答案对1,000,000,007取模的值。 

Input

第一行包含3个整数，N，M，K。 

第二行包含N个整数：a[1], a[2], ..., a[N]。 

Output

输出M个整数到一行，第i个整数为当d=i时满足条件的不同数列{b[n]}的数目mod 1,000,000,007的值。 

Sample Input

3 3 3
3 3 3

Sample Output

7 1 0

HINT

当d=1，{b[n]}可以为：(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1)。 

当d=2，{b[n]}可以为：(2, 2, 2)。 

当d=3，因为{b[n]}必须要有k个数与{a[n]}不同，所以{b[n]}不能为(3, 3, 3)，满足条件的一个都没有。 

对于100%的数据，1<=N,M<=300000, 1<=K<=N, 1<=a[i]<=M。 

Source