JLOI2015 解题报告
JLOI2015 真的不愧是NOI出题组出的，题目难度够吊。不过每一道都是结论题和乱搞题真的很不好玩。。。
首先贴下popoqqq的blog吧
感性的认识就是感觉到部分分是个斐波那契数列的通项公式然后考虑是否能把该式子化成递推式然后矩阵乘法算了。。感觉是超级恶心的一道题了，还得用快速乘法。。。
首先这道题我们先考虑暴力，也就是每个点向父亲跑，我们考虑能否一起做，可以发现在同一个点的骑士可以用一个堆维护一起跳（因为没有改变优先级的操作）然后再用懒标记维护，我们可以直接用一个可合并堆来维护就可以啦
当然这道题用线段树，倍增都是可行的，就是空间比较拙计罢了，需要用一些奇奇怪怪的方法来干
CODE：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
struct node{
node *l,*r;int id,dis;ll s,lx,ly;
node(ll _s,int _id){
l=r=;
s=_s,id=_id,lx=,ly=;dis=;
}
};
inline void update(node* x) {
if (x->l) {
x->l->s*=x->lx;
x->l->s+=x->ly;
x->l->lx*=x->lx;
x->l->ly*=x->lx;
x->l->ly+=x->ly;
}
if (x->r) {
x->r->s*=x->lx;
x->r->s+=x->ly;
x->r->lx*=x->lx;
x->r->ly*=x->lx;
x->r->ly+=x->ly;
}
x->lx=;x->ly=;
}
node* merge(node* x,node *y) {
if (!x) return y;
if (!y) return x;
update(x);update(y);
if (x->s>y->s) swap(x,y);
x->r=merge(x->r,y);
if (!x->l||x->l->dis<x->r->dis) swap(x->l,x->r);
x->dis=x->r?x->r->dis+:;
return x;
}
inline node* del(node *x) {
update(x);
return merge(x->l,x->r);
}
#define maxn 300010
int dep[maxn],fa[maxn],a[maxn],ans[maxn],sum[maxn];
ll h[maxn],v[maxn];
node *root[maxn];
int main(){
freopen("fall.in","r",stdin);
freopen("fall.out","w",stdout);
int n,m;
scanf("%d%d",&n,&m);
for (int i=;i<=n;i++) scanf("%lld",h+i);
dep[]=;
for (int i=;i<=n;i++) {
scanf("%d%d%lld",fa+i,a+i,v+i);
dep[i]=dep[fa[i]]+;
}
for (int i=;i<=m;i++) {
ll s;int c;
scanf("%lld%d",&s,&c);
root[c]=merge(root[c],new node(s,i));
ans[i]=dep[c];
}
for (int i=n;i;i--) {
while (root[i]&&root[i]->s<h[i]) {
sum[i]++;
ans[root[i]->id]-=dep[i];
root[i]=del(root[i]);
}
if (!root[i]) continue;
if (a[i]==) {
root[i]->s+=v[i];
root[i]->ly+=v[i];
}
else {
root[i]->s*=v[i];
root[i]->lx*=v[i];
root[i]->ly*=v[i];
}
root[fa[i]]=merge(root[fa[i]],root[i]);
}
for (int i=;i<=n;i++) printf("%d\n",sum[i]);
for (int i=;i<=m;i++) printf("%d\n",ans[i]);
return ;
}
首先这个其实是求一个代价最小的最大线性无关集合（不会去线性代数把），线性无关集合也就是指在该集合中没有一个向量能由该集合的其他向量组成
所以该集合其实就是一组基，那么我们可以每次用高斯消元判断当前的向量是否能由其他向量组成，如果不行的话就加入答案了
求代价最小就排个序即可
CODE：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define maxn 510
double a[maxn][maxn];
int c[maxn];
const double epx=1e-;
inline bool zero(double x) {return x>-epx&&x<epx;}
int main(){
freopen("purchase.in","r",stdin);
freopen("purchase.out","w",stdout);
int n,m;
scanf("%d%d",&n,&m);
int l=,ans=;
for (int i=;i<=n;i++)
for (int j=;j<=m;j++) scanf("%lf",a[i]+j);
for (int i=;i<=n;i++) scanf("%d",&c[i]);
c[]=;
for (int i=;i<=m;i++) {
int id=;
for (int j=l;j<=n;j++)
if (!zero(a[j][i])&&c[id]>c[j]) id=j;
if (id==) continue;
for (int j=;j<=m;j++) swap(a[l][j],a[id][j]);
swap(c[id],c[l]);
ans+=c[l];
for (int j=l+;j<=n;j++) {
double t=a[j][i]/a[l][i];
for (int k=i;k<=m;k++) a[j][k]-=a[l][k]*t;
}
l++;
}
printf("%d %d\n",l-,ans);
return ;
}
这道题比较奇葩啦
首先我们考虑每一行，可以发现是单调递减的，并且肯定只缺了一个格，所以我们设f[i][j]为第i行缺j的方案数
可得f[i][j]=sigma(f[i-1][k]) k<=j+1
也就是f[i][j]=f[i][j-1]+f[i-1][j+1]
发现这个形式长得很像组合数，也可想求组合数那样看成求路径数。
我们把第i行向右平移i位，那么这个图就变成这样了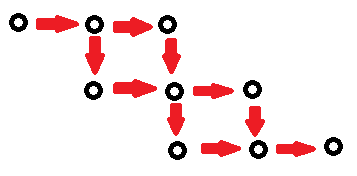
也就是把求这样子的路径方案数。
我们考虑先记下组合数那样的矩形图，再如何去掉左下和右上的点
很明显我们可以将终点按y=-x-1那条线镜面反射即可。
右上角也相似，但可能出现：左上->右下的情况，所以我们还要再去掉这种情况
...
这样推下去
CODE：
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
#define mod 1000000007
#define maxn 3001000
ll fac[maxn],inv[maxn];
int n,m;
inline ll c(int x,int y) {
return fac[x]*1ll*inv[y]%mod*inv[x-y]%mod;
}
inline void _swap1(int &x,int &y) {
swap(x,y);
x--,y++;
}
inline void _swap2(int &x,int &y) {
swap(x,y);
x+=m+,y-=m+;
}
int main(){
freopen("pwn.in","r",stdin);
freopen("pwn.out","w",stdout);
scanf("%d%d",&n,&m);
fac[]=fac[]=;
inv[]=inv[]=;
for (int i=;i<=n+n+m+;i++) {
fac[i]=fac[i-]*i%mod;
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
}
for (int i=;i<=n+m+n+;i++) (inv[i]=inv[i]*inv[i-])%=mod;
int x=n+m+,y=n;
ll ans=c(x+y,y);
for (;;) {
_swap1(x,y);
if (x<||y<) break;
(ans-=c(x+y,y))%=mod;
_swap2(x,y);
if (x<||y<) break;
(ans+=c(x+y,y))%=mod;
}
x=n+m+,y=n;
for (;;) {
_swap2(x,y);
if (x<||y<) break;
(ans-=c(x+y,y))%=mod;
_swap1(x,y);
if (x<||y<) break;
(ans+=c(x+y,y))%=mod;
}
printf("%d\n",(ans+mod)%mod);
return ;
}
这是一个叫斯坦纳树的东西= =，以前知道但没写过，今天终于写了一次了
首先我们可以记f[i][j]为点的联通状态为i，经过点j的距离最小值，那么有两种状态转移
i的转移f[i][j]=max(f[k][j]+f[i^k][j])k为i的子集
j的转移：我们先求出i的转移，然后一边spfa即可
这样可以证明是正确的
这样我们就求出了一组点的答案，那么多组点我们可以用一个dp来合并答案
写起来还是挺舒服的，很多东西都能用这个东西解决，插头dp啊什么的
CODE：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
#define maxk 1030
#define maxn 1100000
#define maxm 3100
#define inf 0x7fffffff
struct edges{
int to,next,dist;
}edge[maxm*];
int next[maxk],l;
inline void addedge(int x,int y,int z) {
edge[++l]=(edges){y,next[x],z};next[x]=l;
}
typedef pair<int,int> ii;
#define fi first
#define se second
int f[maxk][maxk],n,p,a[],c[];
priority_queue<ii,vector<ii>,greater<ii> > q;
bool b[maxk];
inline void dij(){
for (int i=;i<<<p;i++)
for (int j=;j<=n;j++) f[i][j]=inf;
for (int i=;i<p;i++) f[<<i][a[i+]]=;
for (int i=;i<<<p;i++) {
while (!q.empty()) q.pop();
memset(b,,sizeof(b));
for (int j=(i-)&i;j>;j=(j-)&i)
for (int k=;k<=n;k++) f[i][k]=min(f[i][k],f[j][k]+f[i^j][k]);
int *dist=f[i];
for (int j=;j<=n;j++) {
if (dist[j]==inf) continue;
q.push(ii(dist[j],j));
}
int cnt=;
while (!q.empty()) {
ii u=q.top();q.pop();
if (b[u.se]) continue;
b[u.se]=;cnt++;
if (cnt==n) break;
for (int i=next[u.se];i;i=edge[i].next)
if (edge[i].dist+dist[u.se]<dist[edge[i].to]){
dist[edge[i].to]=edge[i].dist+dist[u.se];
q.push(ii(dist[edge[i].to],edge[i].to));
}
}
}
}
int g[maxk],d[];
inline int get(int x) {
int ans=;
for (int i=;x;i++,x>>=) if (x&) ans|=d[i];
return ans;
}
int main(){
freopen("channel.in","r",stdin);
freopen("channel.out","w",stdout);
int m;
scanf("%d%d%d",&n,&m,&p);
for (int i=;i<=m;i++) {
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
addedge(u,v,w);
addedge(v,u,w);
}
for (int i=;i<=p;i++) scanf("%d%d",c+i,a+i);
dij();
for (int i=;i<=p;i++) d[c[i]]|=<<(i-);
for (int i=;i<<<p;i++) {
g[i]=inf;
int x=get(i);
for (int j=;j<=n;j++) g[i]=min(g[i],f[x][j]);
}
for (int i=;i<<<p;i++)
for (int j=(i-)&i;j>;j=(j-)&i)
g[i]=min(g[i],g[j]+g[i^j]);
printf("%d\n",g[(<<p)-]);
return ;
}
T6:[JLOI2015]战争调度
这道题还是挺不错的，jloi考了好多要让你算空间的题- -
记f[i][j][k]为第i个节点祖先状态为j有k个儿子选择战争的最小答案，那么我们考虑一下这样的状态数以及转移复杂度
第i层的节点祖先状态有2^i儿子数有2^n-i一共有2^n个状态，所以总状态数为4^n
每个节点的转移是O(k)的，总的时间复杂度就是n*4^n，可以解决本题
这个主要还是得考你对时间和空间复杂度的分析= =
CODE：
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
typedef pair<int,int>ii;
typedef pair<int,ii> iii;
#define maxn 1030
int n,m,w[][maxn][],ans;
map<iii,int> ma;
int dfs(int x,int y,int z,int size) {
if (ma.find(iii(x,ii(y,z)))!=ma.end()) return ma[iii(x,ii(y,z))];
int s=;
if (x>=(<<(n-))) {
x-=(<<(n-))-;
for (int i=;i<n-;i++) s+=((y>>i)&)==z?w[z][x][i]:;
ma[iii(x+(<<(n-))-,ii(y,z))]=s;
return s;
}
for (int i=;i<=z;i++) {
if (i>(size>>)||z-i>(size>>)) continue;
s=max(s,max(dfs(x<<,y<<,i,size>>)+dfs((x<<)^,y<<,z-i,size>>),dfs(x<<,(y<<)^,i,size>>)+dfs((x<<)^,(y<<)^,z-i,size>>)));
}
ma[iii(x,ii(y,z))]=s;
return s;
}
int main(){
freopen("war.in","r",stdin);
freopen("war.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i=;i<=<<(n-);i++)
for (int j=;j<n-;j++) scanf("%d",w[][i]+j);
for (int i=;i<=<<(n-);i++)
for (int j=;j<n-;j++) scanf("%d",w[][i]+j);
for (int i=;i<=m;i++) ans=max(ans,dfs(,,i,<<(n-)));
printf("%d\n",ans);
}
好啦总结一下这套题吧= =
首先我觉得出得太noi化了没有省选的感觉，但又没有noi那么难，有种四不像的感觉
很多题目的想法都很值得学习，而且题解的ppt上的总结写得非常好
总的来说还是值得一刷的
JLOI2015 解题报告的更多相关文章
- CH Round #56 - 国庆节欢乐赛解题报告
最近CH上的比赛很多,在此会全部写出解题报告,与大家交流一下解题方法与技巧. T1 魔幻森林 描述 Cortana来到了一片魔幻森林,这片森林可以被视作一个N*M的矩阵,矩阵中的每个位置上都长着一棵树 ...
- 二模13day1解题报告
二模13day1解题报告 T1.发射站(station) N个发射站,每个发射站有高度hi,发射信号强度vi,每个发射站的信号只会被左和右第一个比他高的收到.现在求收到信号最强的发射站. 我用了时间复 ...
- BZOJ 1051 最受欢迎的牛 解题报告
题目直接摆在这里! 1051: [HAOI2006]受欢迎的牛 Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 4438 Solved: 2353[S ...
- 习题：codevs 2822 爱在心中 解题报告
这次的解题报告是有关tarjan算法的一道思维量比较大的题目(真的是原创文章,希望管理员不要再把文章移出首页). 这道题蒟蒻以前做过,但是今天由于要复习tarjan算法,于是就看到codevs分类强联 ...
- 习题：codevs 1035 火车停留解题报告
本蒟蒻又来写解题报告了.这次的题目是codevs 1035 火车停留. 题目大意就是给m个火车的到达时间.停留时间和车载货物的价值,车站有n个车道,而火车停留一次车站就会从车载货物价值中获得1%的利润 ...
- 习题： codevs 2492 上帝造题的七分钟2 解题报告
这道题是受到大犇MagHSK的启发我才得以想出来的,蒟蒻觉得自己的代码跟MagHSK大犇的代码完全比不上,所以这里蒟蒻就套用了MagHSK大犇的代码(大家可以关注下我的博客,友情链接就是大犇MagHS ...
- 习题：codevs 1519 过路费 解题报告
今天拿了这道题目练练手,感觉自己代码能力又增强了不少: 我的思路跟别人可能不一样. 首先我们很容易就能看出,我们需要的边就是最小生成树算法kruskal算法求出来的边,其余的边都可以删掉,于是就有了这 ...
- NOIP2016提高组解题报告
NOIP2016提高组解题报告 更正:NOIP day1 T2天天爱跑步 解题思路见代码. NOIP2016代码整合
- LeetCode 解题报告索引
最近在准备找工作的算法题,刷刷LeetCode,以下是我的解题报告索引,每一题几乎都有详细的说明,供各位码农参考.根据我自己做的进度持续更新中...... ...
随机推荐
- 配置Linux Kernel时make menuconfig执行流程分析
在编译内核前,一般是根据已有的配置文件(一般在内核根目录下的arch/arm/configs/文件夹下,把该目录下的xxx_defconfig文件拷贝到内核根目录下,并重命名为.config)来 ...
- Redis的启动
http://www.cnblogs.com/goodspeed/archive/2012/10/18/2729615.html http://blog.csdn.net/yulei_qq/artic ...
- C语言－while循环
循环是结构化程序设计的基本结构之一,它和顺序控制.选择结构共同作为各种复杂程序的基本构造单元(摘自谭浩强的<C程序设计>. 一.while循环: 1.使用while循环控制输出0到9十个数 ...
- FB面经 Prepare: All Palindromic Substrings
Given a string, calculate how many substring is palindrome. Ignore non-char characters. Ignore case; ...
- UVa 10551 - Basic Remains
题目大意:关于大数的mod和进制转换,直接使用Java的BigInteger类,正在copy式学习中... import java.io.*; import java.util.*; import j ...
- java系列--JSP的属性和内置对象
一.JSP指令: <%@ 指令名 属性=" " %> 1.page指令 import属性 errorPage属性 language属性 session属性 isErro ...
- php sprintf函数
定义和用法 sprintf() 函数把格式化的字符串写写入一个变量中.sprintf(format,arg1,arg2,arg++) 参数 描述 format 必需.转换格式. arg1 必需.规定插 ...
- 怎么使用OCR文字识别软件图像压缩功能
ABBYY FineReader是一款非常实用的OCR文字识别软件,在使用ABBYY FineReader保存文档时可以选择图像格式和压缩方法,通过图像压缩可以减小文件的大小,图像压缩方法视压缩率和数 ...
- OBJECT和EMBED标签
一.介绍: 我们要在网页中正常显示flash内容,那么页面中必须要有指定flash路径的标 签.也就是OBJECT和EMBED标签.OBJECT标签是用于windows平台的IE浏览器的,而EMBED ...
- xhtmlrenderer渲染pdf，中文换行
在实际开发中,发现在table中显示中文,渲染出来的pdf,中文内容不自动换行.经过搜索发现了一种解决方案,如下: 重写Breaker,修改right计算方式 /* * Breaker.java * ...