编辑距离算法详解：Levenshtein Distance算法

算法基本原理：假设我们可以使用d[ i , j ]个步骤（可以使用一个二维数组保存这个值），表示将串s[ 1…i ] 转换为 串t [ 1…j ]所需要的最少步骤个数，那么，在最基本的情况下，即在i等于0时，也就是说串s为空，那么对应的d[0,j] 就是 增加j个字符，使得s转化为t，在j等于0时，也就是说串t为空，那么对应的d[i,0] 就是 减少 i个字符，使得s转化为t。

然后我们考虑一般情况，加一点动态规划的想法，我们要想得到将s[1..i]经过最少次数的增加，删除，或者替换操作就转变为t[1..j]，那么我们就必须在之前可以以最少次数的增加，删除，或者替换操作，使得现在串s和串t只需要再做一次操作或者不做就可以完成s[1..i]到t[1..j]的转换。所谓的“之前”分为下面三种情况：

1）我们可以在k个操作内将 s[1…i] 转换为 t[1…j-1]

2）我们可以在k个操作里面将s[1..i-1]转换为t[1..j]

3）我们可以在k个步骤里面将 s[1…i-1] 转换为 t [1…j-1]

针对第1种情况，我们只需要在最后将 t[j] 加上s[1..i]就完成了匹配，这样总共就需要k+1个操作。

针对第2种情况，我们只需要在最后将s[i]移除，然后再做这k个操作，所以总共需要k+1个操作。

针对第3种情况，我们只需要在最后将s[i]替换为 t[j]，使得满足s[1..i] == t[1..j]，这样总共也需要k+1个操作。而如果在第3种情况下，s[i]刚好等于t[j]，那我们就可以仅仅使用k个操作就完成这个过程。

最后，为了保证得到的操作次数总是最少的，我们可以从上面三种情况中选择消耗最少的一种最为将s[1..i]转换为t[1..j]所需要的最小操作次数。

算法基本步骤：

（1）构造 行数为m+1 列数为 n+1 的矩阵 , 用来保存完成某个转换需要执行的操作的次数，将串s[1..n] 转换到 串t[1…m] 所需要执行的操作次数为matrix[n][m]的值；

（2）初始化matrix第一行为0到n，第一列为0到m。

Matrix[0][j]表示第1行第j-1列的值，这个值表示将串s[1…0]转换为t[1..j]所需要执行的操作的次数，很显然将一个空串转换为一个长度为j的串，只需要j次的add操作，所以matrix[0][j]的值应该是j，其他值以此类推。

（3）检查每个从1到n的s[i]字符；

（4）检查每个从1到m的s[i]字符；

（5）将串s和串t的每一个字符进行两两比较，如果相等，则让cost为0，如果不等，则让cost为1（这个cost后面会用到）;

(6)a、如果我们可以在k个操作里面将s[1..i-1]转换为t[1..j]，那么我们就可以将s[i]移除，然后再做这k个操作，所以总共需要k+1个操作。

b、如果我们可以在k个操作内将 s[1…i] 转换为 t[1…j-1] ，也就是说d[i,j-1]=k，那么我们就可以将 t[j] 加上s[1..i]，这样总共就需要k+1个操作。

c、如果我们可以在k个步骤里面将 s[1…i-1] 转换为 t [1…j-1]，那么我们就可以将s[i]转换为 t[j]，使得满足s[1..i] == t[1..j]，这样总共也需要k+1个操作。（这里加上cost，是因为如果s[i]刚好等于t[j]，那么就不需要再做替换操作，即可满足，如果不等，则需要再做一次替换操作，那么就需要k+1次操作）

因为我们要取得最小操作的个数，所以我们最后还需要将这三种情况的操作个数进行比较，取最小值作为d[i,j]的值；

d、然后重复执行3,4,5,6，最后的结果就在d[n,m]中；

图解：

图解过程如下：

step 1：初始化如下矩阵

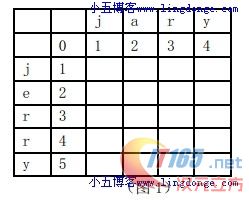
step 2：从源串的第一个字符（“j”）开始，从上至下与目标串进行对比

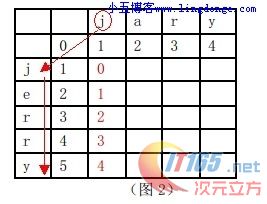
如果两个字符相等，则在从此位置的左加1，上加1，左上加0三个位置中取出最小的值；若不等，则在从此位置的左，上，左上三个位置中取出最小的值再加上1；

第一次，源串第一个字符“j” 与目标串的“j”对比,左，上，左上三个位置中取出最小的值0，因为两字符相等，所以加上0；接着，依次对比“j”→“e”，“j”→“r”，“j”→“r”，，“j”→“y” 到扫描完目标串。

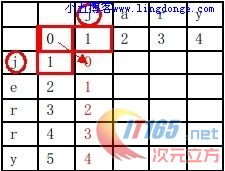
step 3：遍历整个源串与目标串对比：

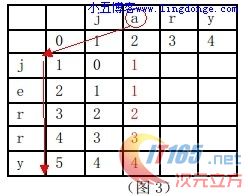
step 4：扫描完最后一列，则最后一个为最短编辑距离：

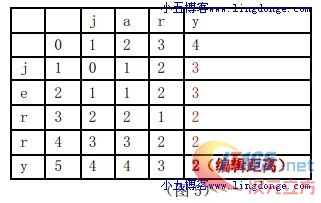
求出编辑距离，那么两个字符串的相似度 Similarity = (Max(x,y) - Levenshtein)/Max(x,y)，其中 x,y 为源串和目标串的长度。

核心代码如下：

 public class LevenshteinDistance
    {
        private static LevenshteinDistance _instance = null;
        public static LevenshteinDistance Instance
        {
            get
            {
                if (_instance == null)
                {
                    return new LevenshteinDistance();
                }
                return _instance;
            }
        }

        public int LowerOfThree(int first, int second, int third)
        {
            int min = first;
            if (second < min)
                min = second;
            if (third < min)
                min = third;
            return min;
        }

        public int Compare_Distance(string str1, string str2)
        {
            int[,] Matrix;
            int n = str1.Length;
            int m = str2.Length;

            int temp = ;
            char ch1;
            char ch2;
            int i = ;
            int j = ;
            if (n == )
            {
                return m;
            }
            if (m == )
            {

                return n;
            }
            Matrix = new int[n + , m + ];

            for (i = ; i <= n; i++)
            {
                Matrix[i, ] = i;
            }

            for (j = ; j <= m; j++)
            {
                Matrix[, j] = j;
            }

            for (i = ; i <= n; i++)
            {
                ch1 = str1[i - ];
                for (j = ; j <= m; j++)
                {
                    ch2 = str2[j - ];
                    if (ch1.Equals(ch2))
                    {
                        temp = ;
                    }
                    else
                    {
                        temp = ;
                    }
                    Matrix[i, j] = LowerOfThree(Matrix[i - , j] + , Matrix[i, j - ] + , Matrix[i - , j - ] + temp);
                }
            }

            return Matrix[n, m];

        }

        public decimal LevenshteinDistancePercent(string str1, string str2)
        {
            int maxLenth = str1.Length > str2.Length ? str1.Length : str2.Length;
            int val = Compare_Distance(str1, str2);
            return  - (decimal)val / maxLenth;
        }
    }