[computer graphics]简单光照模型(Phong和Blinn-Phong)和明暗处理

简单光照模型(Phong和Blinn-Phong)和明暗处理

支持点光源和平行光，是一种简单光照模型，它将光照分解成了三个部分，分别为

• 漫反射
• 镜面反射
• 环境光

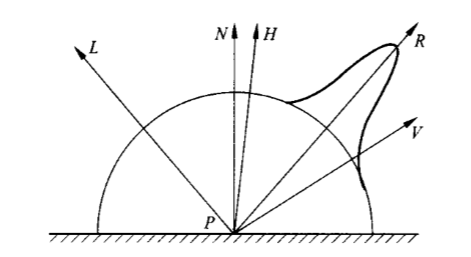
如图所示，是一个简单的几何模型。

• \(L\)是光源方向
• \(N\)是法线方向
• \(R\)是反射方向
• \(V\)是视线方向
• \(H\)是\(L\)和\(V\)的平分
• 所有向量都是单位向量

理想漫反射

当光源来自一个方向时，漫反射均匀地向各个方向传播，与视点无关，是由物体表面粗糙不平引起的，漫反射的空间分布是均匀的，也就是说不论从哪个方向看去，同一个点的漫反射光强都是一样的。物体上的点\(P\)，法向量为\(N\)，入射光强度为\(I_p\)，\(L\)为\(P\)指向光源的方向。如果所有所有的向量都是单位向量，那么有

\[I_d = I_pK_d\cdot(L\cdot N)
\]

其中\(K_d=(K_{dr},K_{dg},K_{db})\)这三个分量分别是RGB三原色的漫反射系数，可以反应物体的颜色。同样的\(I_p=(I_r,I_g,I_b)\)可以通过分量来设置光源的颜色。

镜面反射

对于理想镜面，反射光集中在一个方向，并遵守反射定律。对于一般的光滑表面，反射光则集中在一个范围内，且反射定律决定的方向光强最大。所以从不同位置观察到的镜面反射光强不同。镜面反射光可表示为

\[I_s = I_pK_s(R\cdot V)^{n}
\]

\(R \cdot V\)计算的是反射方向和视线方向的夹角，夹角越小，强度越大。\(n\)是反射指数，反应了物体的表面的光滑程度，一般1-2000。\(n\)越大约光滑，因为n越大，例如2000，那么当夹角很小时，例如很接近1，如0.9，但是经过2000乘方，就变得很小了，这意味着只有无限接近反射方向，才能看到高光，其他方向不行，这就表示物体很光滑。反过来，\(n\)很小那么移动一点角度，也能看到衰弱的高光，所以光斑会比较明显。

在镜面反射模型中，最终要的是计算R的方向，\(R\)可以通过入射方向和法线方向计算出来

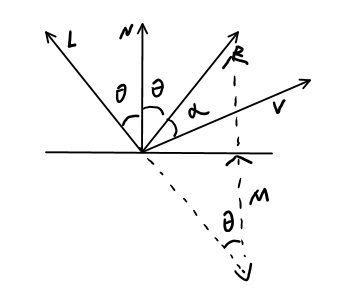
因为这里的向量都是单位向量，只有方向不一致

\[\begin{aligned}
||L||\cos\theta &= ||M||=\cos\theta\\
&M和N的方向一致\\
R &= -L+2M \\
&=2N\cos\theta-L\\
&=2N\cdot(N\cdot L)-L
\end{aligned}
\]

高光区域只反映光源的颜色，漫反射才能设定物体的颜色。

环境光

光源间接对物体施加的明暗影响，在物体和环境之间多次反射。在简单光照模型中进行了简化，通常用一个常数来模拟环境光

\[I = I_aK_a
\]

\(I_a\)是环境光强，\(K_a\)为物体对环境光的反射系数。

Phong模型

\[I = I_aK_a +I_pK_d\cdot(L\cdot N)+I_pK_s(R\cdot V)^{n}
\]

Phong模型是上述三种因素的叠加，其中\(R\)的计算比较费时，需要对每一点计算一次\(R\)的值。

Blinn-Phong模型

由于Phong模型计算较为耗时，后来提出了一种对Phong模型的修改，Blinn-Phong模型。

假设:

1. 光源在无穷远处，光线的方向L为常数（这就意味着，对物体上所有点来说，光线的方向都是一致的，正常情况应该是光源到点的向量，每个点的光照方向都不一致）
2. 视点在无穷远处，视线的防线V为常数（这个同理）
3. 此模型针对高光部分进行了修改，\(R\cdot V\)的计算用\(H\cdot N\)近似，其中\(H=(L+V)/||L+V||\)，也就是\(L\)和\(V\)的平分向量。当\(V\)接近\(R\)的时候，\(H\)也接近\(N\)，符号高光的规律。对于所有点，\(H\)只需计算一次。

所以Blinn-Phong模型的可以表示成：

\[I = I_aK_a +I_pK_d\cdot(L\cdot N)+I_pK_s(H\cdot N)^{n}
\]

（图片中应该采用了明暗处理，不仅是光照模型）

明暗处理

如今的物体大多数用多边形表示，一个多边形的法线方向一致，因此一个多边形内部的像素相同，而在邻接出可能会有突变，感觉不连续。为了让过度平滑，基本思想是：对多边形的顶点计算合适的光强度，在内部进行均匀插值。其中有两种主要的做法：

• 计算物体表面多边形顶点的光强，然后插值，求多边形内部光强。
• 对内部点的法向量进行插值，而顶点的法向量用相邻多边形的法向量的平均值得到。

Gouraud明暗处理（双线性光强插值）

基本算法

1. 计算多边形顶点的平均法向量
2. 用Phong模型计算顶点的平均强度
3. 插值计算离散边上的各点光强
4. 插值计算多边形区域内的各点光强

计算速度比简单光照模型有了很大的提高，解决了颜色突变问题，但是镜面反射效果不理想。

Phong明暗处理（双线性法向量插值）

和Gouraud方法基本类似，只不过是对法向量插值。多边形顶点的法向量用相邻多边形的法向量的平均值。而内部每个点都要计算法向量，用顶点的法向量插值得到。

这种做法效果好，可以产生正确的高光，但是计算量很大。

• [1]维基百科
• [2]计算机图形学基础教程 胡事民