牛牛的DRB迷宫（DP、二进制编码器）

牛牛的DRB迷宫I

链接：https://ac.nowcoder.com/acm/contest/3004/A
来源：牛客网

题目描述

牛牛有一个n*m的迷宫，对于迷宫中的每个格子都为'R','D','B'三种类型之一，'R'表示处于当前的格子时只能往右边走'D'表示处于当前的格子时只能往下边走，而'B'表示向右向下均可以走。

我们认为迷宫最左上角的坐标为(1,1)，迷宫右下角的坐标为(n,m)，除了每个格子有向右移动以及向下移动的限制之外，你也不能够走出迷宫的边界。

牛牛现在想要知道从左上角走到右下角不同种类的走法共有多少种，请你告诉牛牛从(1,1)节点移动到(n,m)节点共有多少种不同的移动序列，请你输出方案数对10⁹+7取余数后的结果。

我们认为两个移动序列是不同的，当且仅当移动序列的长度不同，或者在某一步中采取了不同的移动方式。

输入描述:

第一行输入两个正整数n,m(1≤n,m≤50)表示迷宫的大小是n行m列。

接下来n行，每行输入一个长度为m的字符串，字符串中仅包含大写字母'D','R','B'。

输出描述:

输出一行一个整数，表示方案数对10⁹+7取余数后的结果。

输入

RBBBR
BBBBB
BBBDB
BDBBB
RBBBB

输出

这个题比较简单，是经典的走格子DP（棋盘型DP）。时空复杂度O(nm)

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <stack>
 #include <queue>
 #include <set>
 #include <map>
 #include <sstream>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const int maxn=1e5+;
 using namespace std;

 char G[][];
 LL dp[][];

 int main()
 {
     #ifdef DEBUG
     freopen("sample.txt","r",stdin);
     #endif

     int n,m;
     scanf("%d %d",&n,&m);
     for(int i=;i<=n;i++)
         scanf("%s",G[i]+);
     dp[][]=;
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=m;j++)
         {
             if(G[i][j-]!='D') dp[i][j]=(dp[i][j]+dp[i][j-])%mod;
             if(G[i-][j]!='R') dp[i][j]=(dp[i][j]+dp[i-][j])%mod;
         }
     }
     printf("%lld\n",dp[n][m]);

     return ;
 }

牛牛的DRB迷宫II

链接：https://ac.nowcoder.com/acm/contest/3004/B
来源：牛客网

题目描述

牛牛有一个n*m的迷宫，对于迷宫中的每个格子都为'R','D','B'三种类型之一，'R'表示处于当前的格子时只能往右边走'D'表示处于当前的格子时只能往下边走，而'B'表示向右向下均可以走。

我们认为迷宫最左上角的坐标为(1,1)，迷宫右下角的坐标为(n,m)，除了每个格子有向右移动以及向下移动的限制之外，你也不能够走出迷宫的边界。

牛牛现在请你设计迷宫，但是要求你设计的迷宫符合他的要求，他要求你设计的迷宫从(1,1)节点移动到(n,m)节点不同的移动序列种类数目≡k(mod10⁹+7)。

请你构造出符合条件的DRB迷宫，但是要求你输出的迷宫的大小不超过50*50，具体输出格式见输出描述及样例。

如果存在多解你可以构造任意符合条件的迷宫，反之如果无解，请输出一行一个字符串"No solution"。

输入描述:

仅一个整数k，你需要构造一个DRB迷宫符合从左上走到右下的方案数≡k(mod10⁹+7)。

输出描述:

请你构造出符合条件的DRB迷宫,但是要求你输出的迷宫的大小不超过50*50。

第一行输出n,m两个整数，中间用空格隔开。

接下来n行，每行输出一个大小为m的字符串，字符串只能包含大写字母'D','R','B'。

如果存在多解你可以构造任意符合条件的迷宫，反之如果无解，请输出一行一个字符串"No solution"。

输入

输出

RBBBR
BBBBB
BBBDB
BDBBB
RBBBB

说明

样例为《牛牛的DRB迷宫I》中的样例反过来。

备注:

≡为同余等号，意为等式两边在对模数取余后的结果相同。

本题为Special Judge类型，只要符合题目要求的答案均可通过。

构造A题中的迷宫，要求方案数整好等于给定的k，可以构造一个二进制编码器，斜对角线上的方案数恰好是1,2,4,8,16,32...，用二进制可以拼出所有的数字，所以一定能造的出来。

题解的图是这样的，即主对角线上的格子都为B，它的上面点为D，下面点为R。那么一开始这样的初始图的方案数为2n-1个。

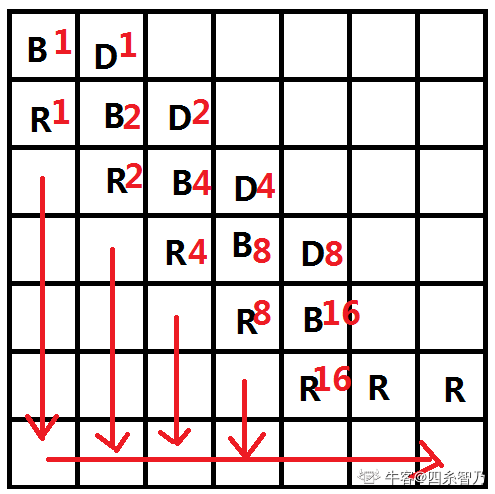
10^9+7的二进制是30位，开G[32][30]，每一列相当于一个二进制位，前面31行是二进制编码器，相当于多加了一行来在判断该二进制位是否为1后通向G[32][30]

前31行:

如果k=25，输出为：

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <stack>
 #include <queue>
 #include <set>
 #include <map>
 #include <sstream>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const int maxn=1e5+;
 using namespace std;

 char G[][];

 int main()
 {
     #ifdef DEBUG
     freopen("sample.txt","r",stdin);
     #endif

     int k;
     scanf("%d",&k);
     for(int i=;i<=-;i++)//前面31行相当于二进制编码器
     {
         for(int j=;j<=;j++)
         {
             if(j<i-) G[i][j]='D';//左方为D
             else if(j<i+) G[i][j]='B';//i和其左右为B
             else G[i][j]='R';//右方为R
         }
     }
     for(int i=;i<=;i++)
     {
         if( !(k&( <<(i-) )) ) G[i+][i]='R';//封路
         G[][i]='R';//加上最后一行
     }
     printf("%d %d\n",,);
     for(int i=;i<=;i++)
         printf("%s\n",G[i]+);

     return ;
 }

-