k-近邻算法采用for循环调参方法

//2019.08.02下午
#机器学习算法中的超参数与模型参数
1、超参数：是指机器学习算法运行之前需要指定的参数，是指对于不同机器学习算法属性的决定参数。通常来说，人们所说的调参就是指调节超参数。
2、模型参数：是指算法在使用过程中需要学习得到的参数，即输入与输出之间映射函数中的参数，它需要通过对于训练数据集训练之后才可以得到。
3、对于KNN算法，它是没有模型参数的，它的k参数就属于典型的超参数。

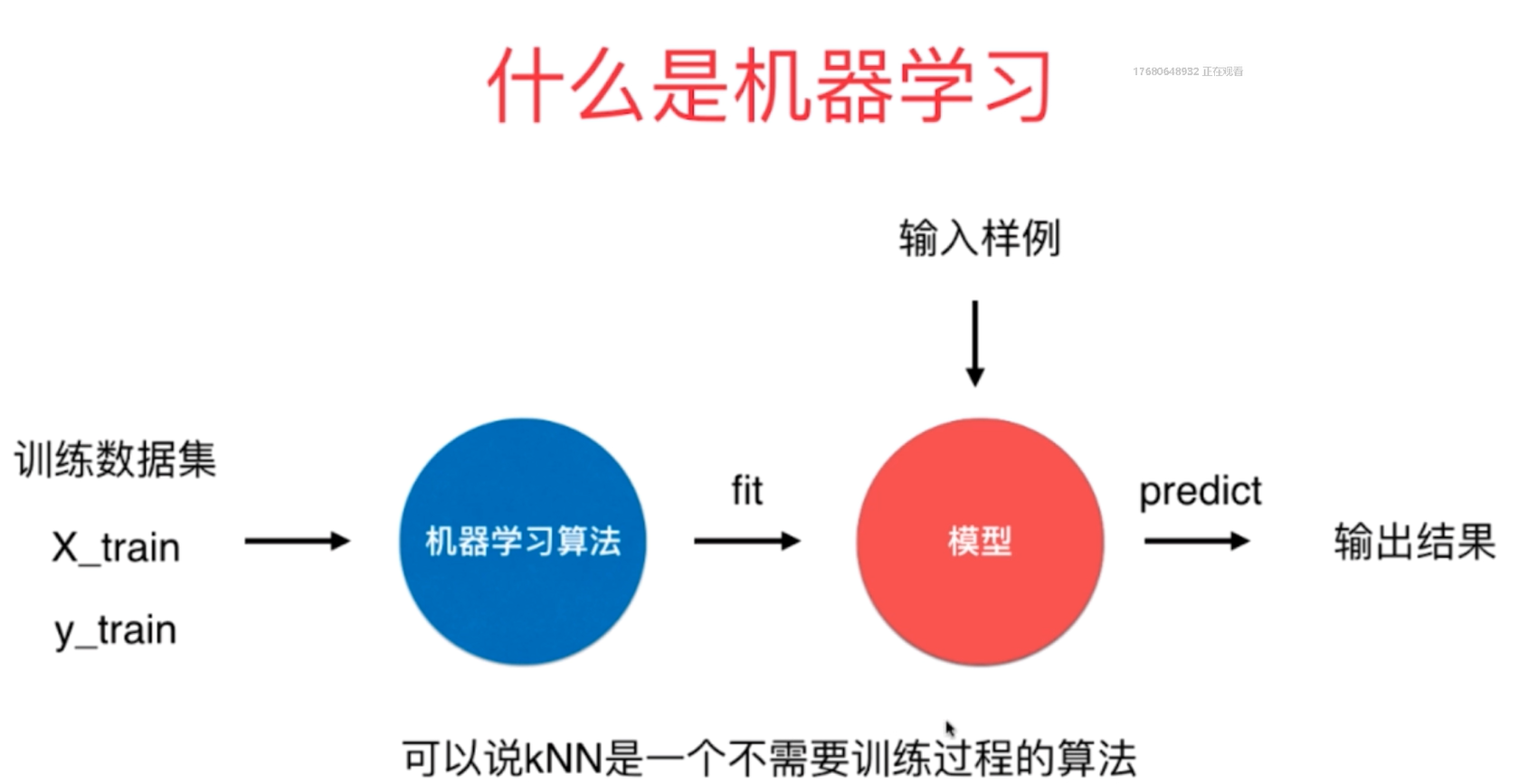
4、好的超参数的选择主要取决于三个方面：
(1)领域知识
(2)经验数值
(3)实验搜索
5、K近邻算法常用的三大超参数：k、weights=("uniform","distance")以及在weights=distance的情况下p参数。

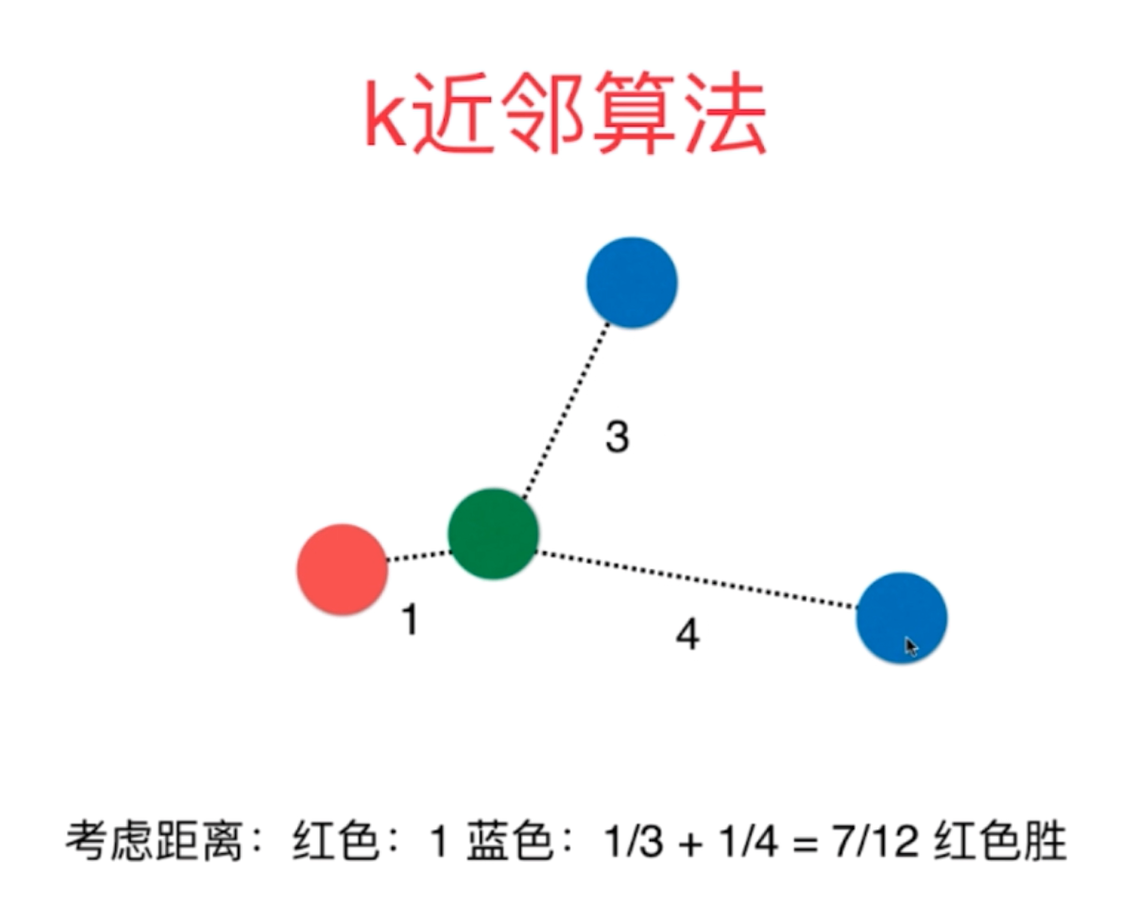
6、K近邻算法超参数调节寻找最优的方法：网络搜索方式举例如下：
#对于KNN算法寻找最佳的超参数k的值以及另外一个超参数weights=uniform/distances,以及在distance的情况下选择出最佳的超参数p的值的大小：
import numpy as np
import matplotlib.pyplot as plt #导入相应的数据可视化模块

#根据训练得到模型的准确率来进行寻找最佳超参数k肯weights
best_method=""
best_score=0.0    
best_k=0
s=[]          #初始定义所需要寻找的超参数
from sklearn.neighbors import KNeighborsClassifier
for method in ["uniform","distance"]:
    for k in range(1,11):              #采用for循环来进行寻找最优的超参数
    KNN=KNeighborsClassifier(n_neighbors=k,weights=method)
    KNN.fit(x_train,y_train) #进行原始数据的训练
    score=KNN.score(x_test,y_test) #直接输出相应的准确度
    s.append(score)
    if score>best_score:
        best_score=score
        best_k=k
        best_method=method        
#数据验证
print("best_method=",best_method)
print("best_k=",best_k)
print("best_score=",best_score)
plt.figure(2)
x=[i for i in range(1,21)]
plt.plot(x,s,"r")
plt.show()

#根据训练得到模型的准确率来进行寻找最佳超参数k以及在weights=distance的情况下寻找最优的参数p
best_p=0
best_score=0.0
best_k=0
s=[]                   #初始化超参数
from sklearn.neighbors import KNeighborsClassifier
for k in range(1,11):
     for p in range(1,6):
     KNN=KNeighborsClassifier(n_neighbors=k,weights="distance",p=p)
     KNN.fit(x_train,y_train) #进行原始数据的训练
     score=KNN.score(x_test,y_test) #直接输出相应的准确度
     s.append(score)
    if score>best_score:
       best_score=score #利用网络搜索方式来寻找最高准确率下的最佳超参数
       best_k=k
       best_p=p
#数据验证
print("best_p=",best_p)
print("best_k=",best_k)
print("best_score=",best_score)
plt.figure(2)
s1=[]
x=[i for i in range(1,6)]
for i in range(1,11):
   s1=s[(i*5-5):(5*i)]
   plt.plot(x,s1,label=i)
   plt.legend(loc=2)
plt.show()

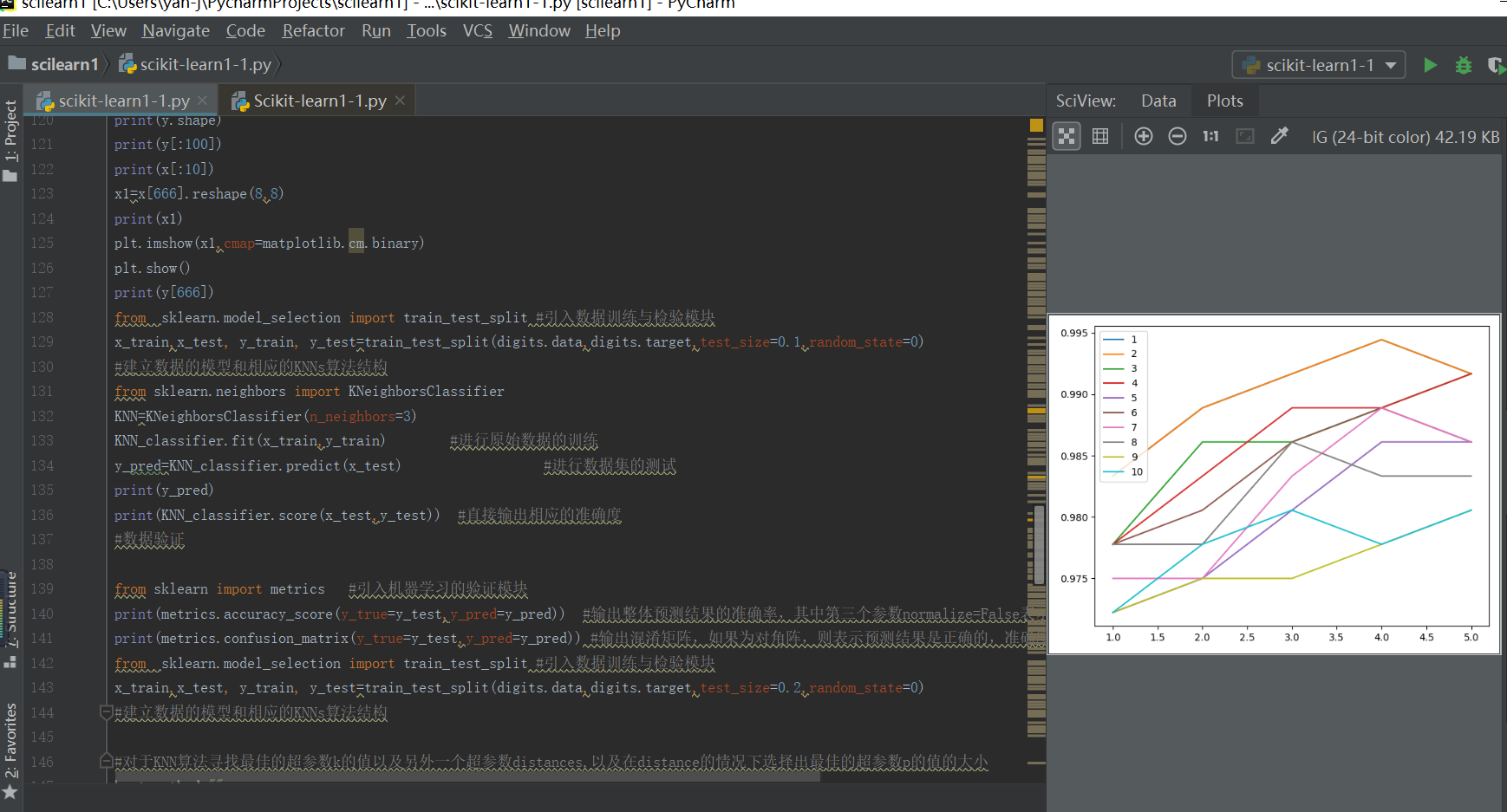
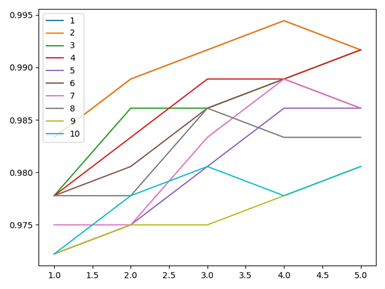
输出结果如下所示：（不同的k和p参数情况下的准确度输出结果）