pytorch梯度下降法讲解（非常详细）

pytorch随机梯度下降法
1、梯度、偏微分以及梯度的区别和联系
(1)导数是指一元函数对于自变量求导得到的数值，它是一个标量，反映了函数的变化趋势；
(2)偏微分是多元函数对各个自变量求导得到的，它反映的是多元函数在各个自变量方向上的变化趋势，也是标量；
(3)梯度是一个矢量，是有大小和方向的，其方向是指多元函数增大的方向，而大小是指增长的趋势快慢。

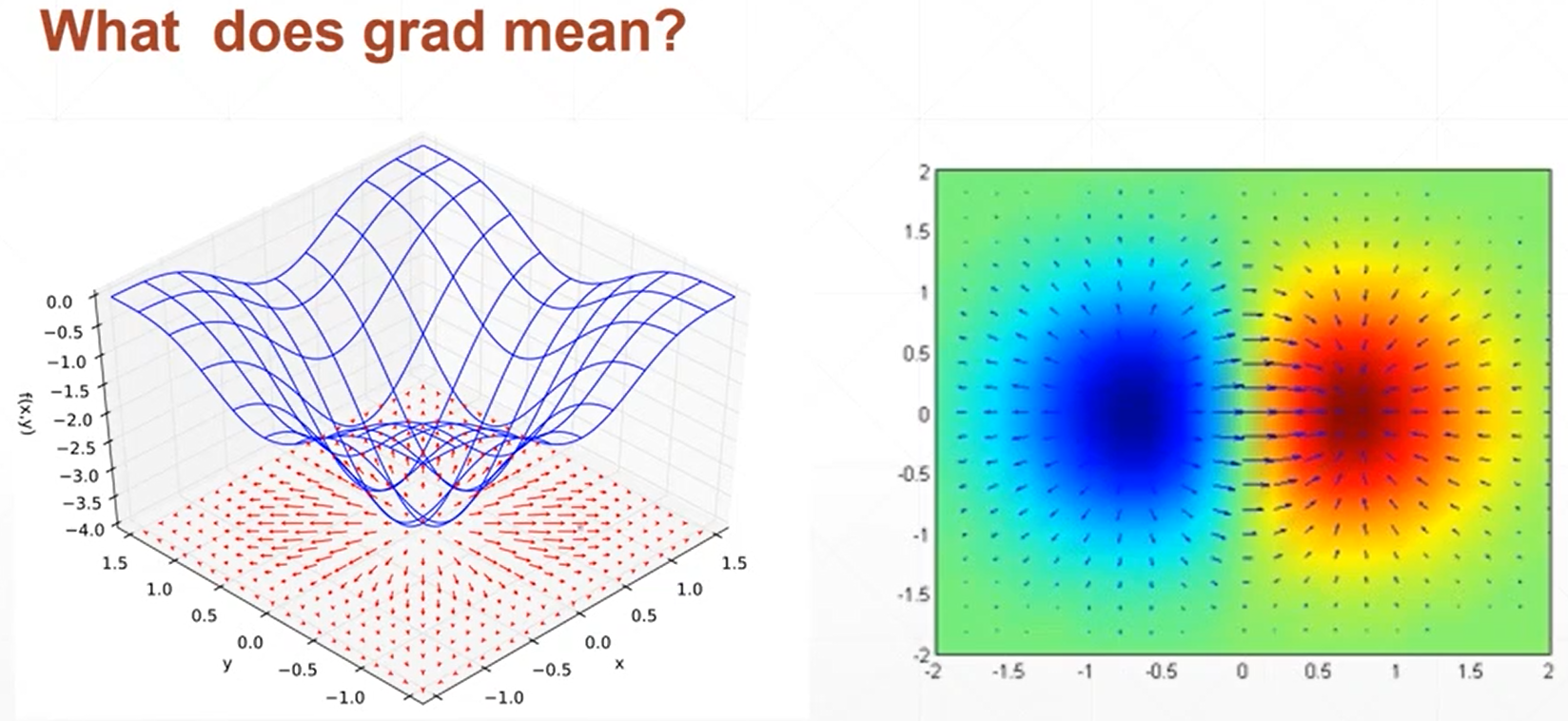
2、在寻找函数的最小值的时候可以利用梯度下降法来进行寻找，一般会出现以下两个问题局部最优解和铵点(不同自变量的变化趋势相反，一个处于极小，一个处于极大)

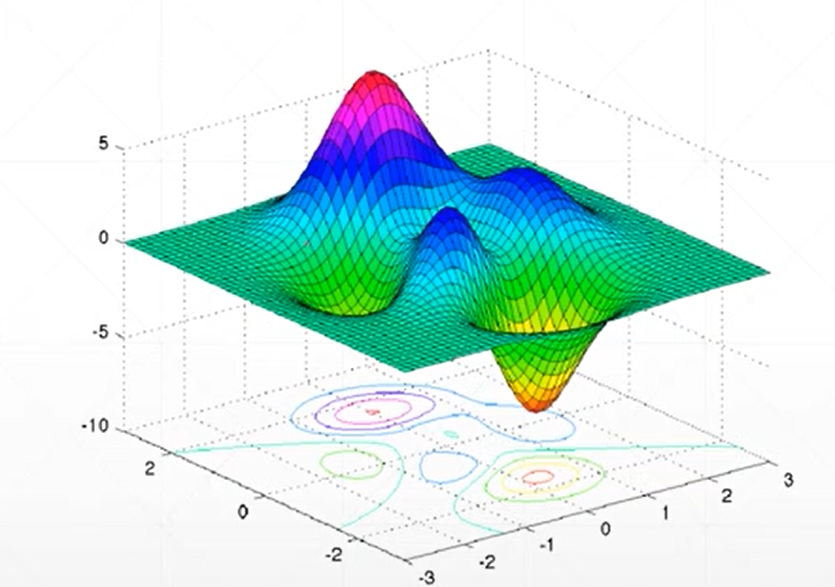
图
3、初始状态、学习率和动量(如何逃出局部最优解)是全部寻优的三个重要影响因素

图
4、常见函数的梯度计算基本和一元函数导数是一致的

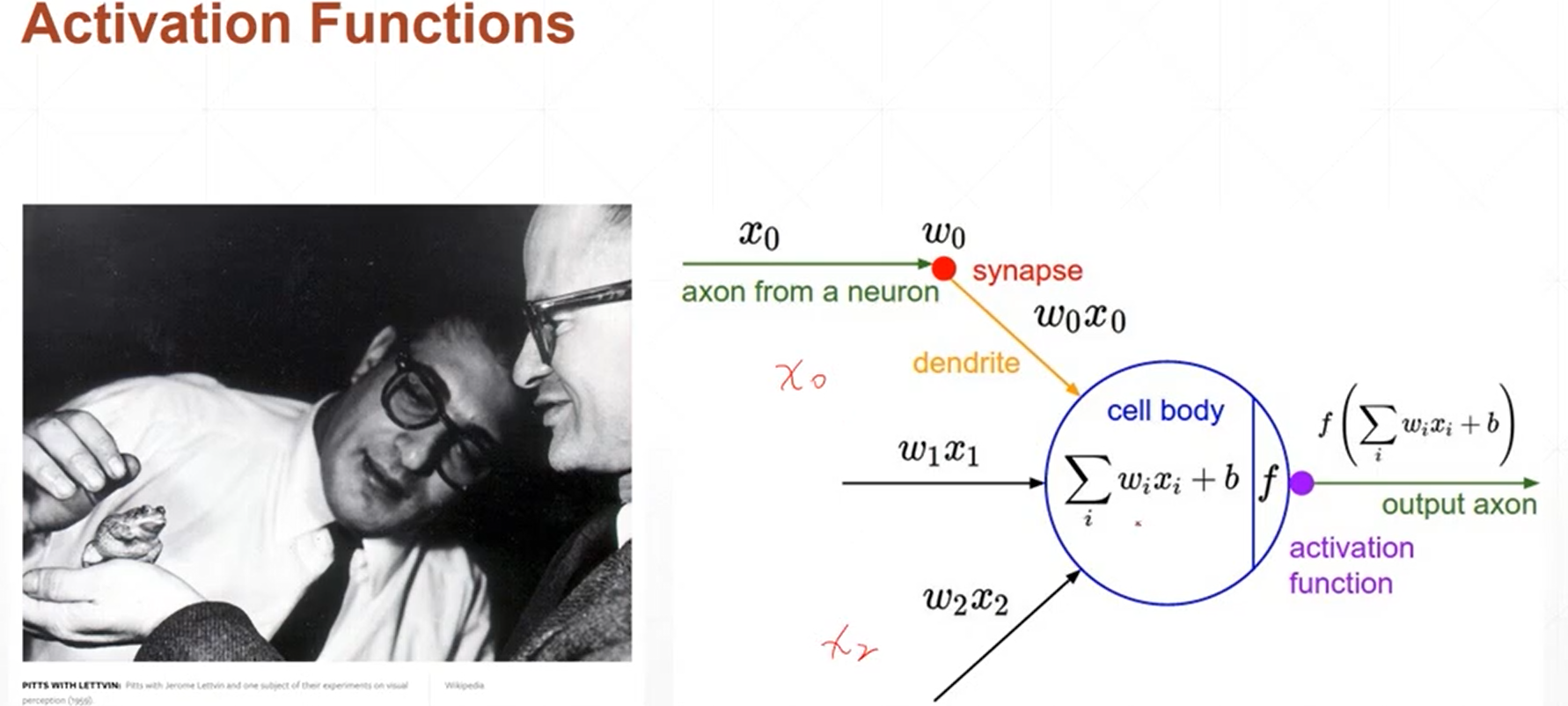
5、常见的激活函数主要有三种：
(1)sigmoid函数

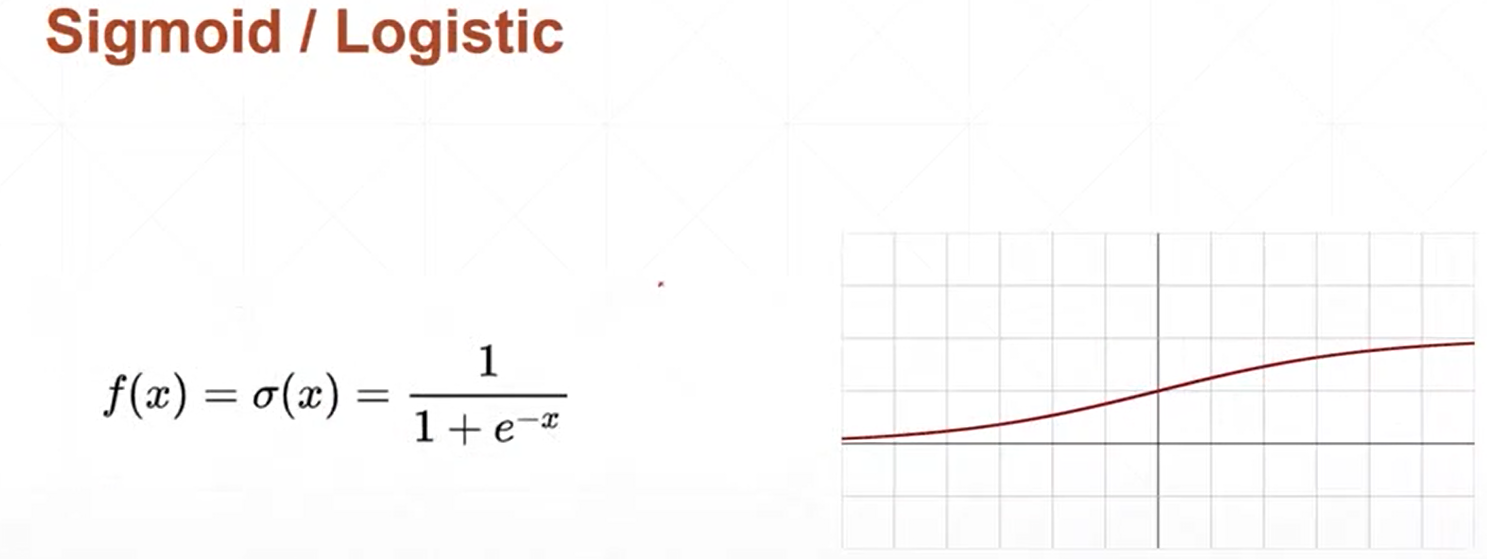
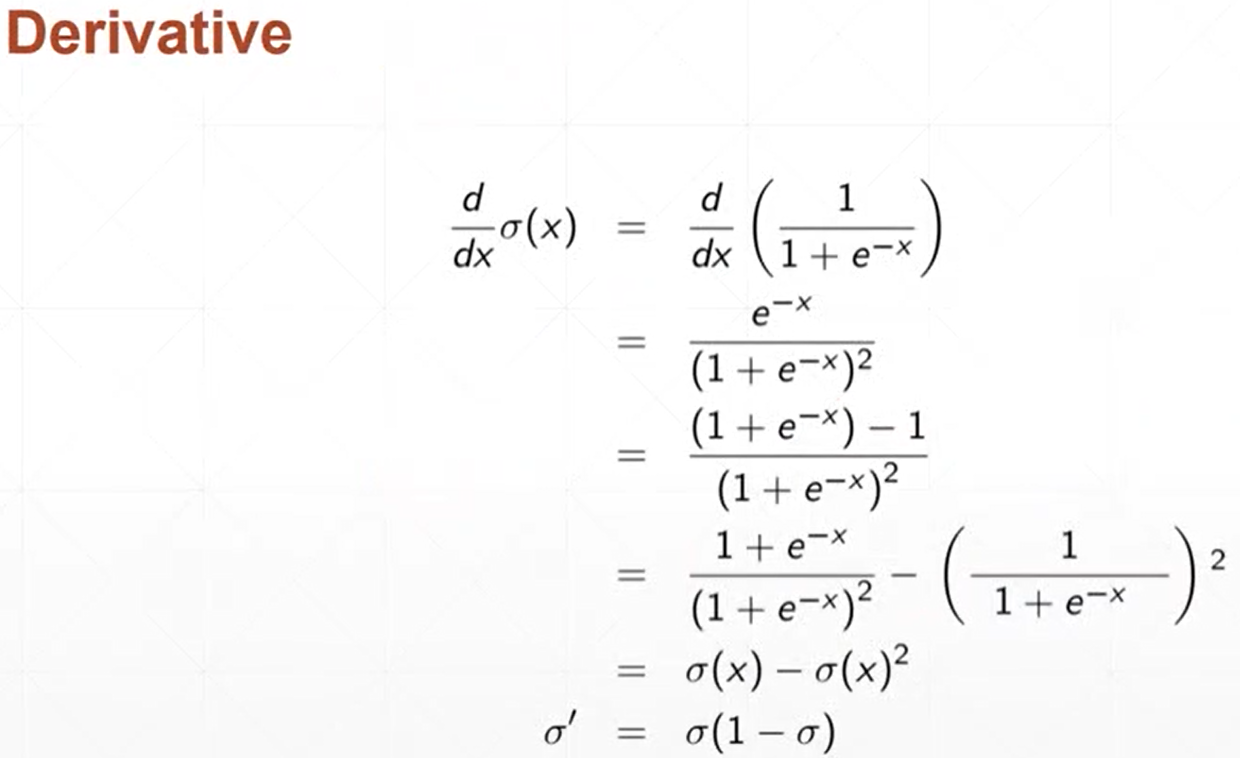
(2)tanh函数

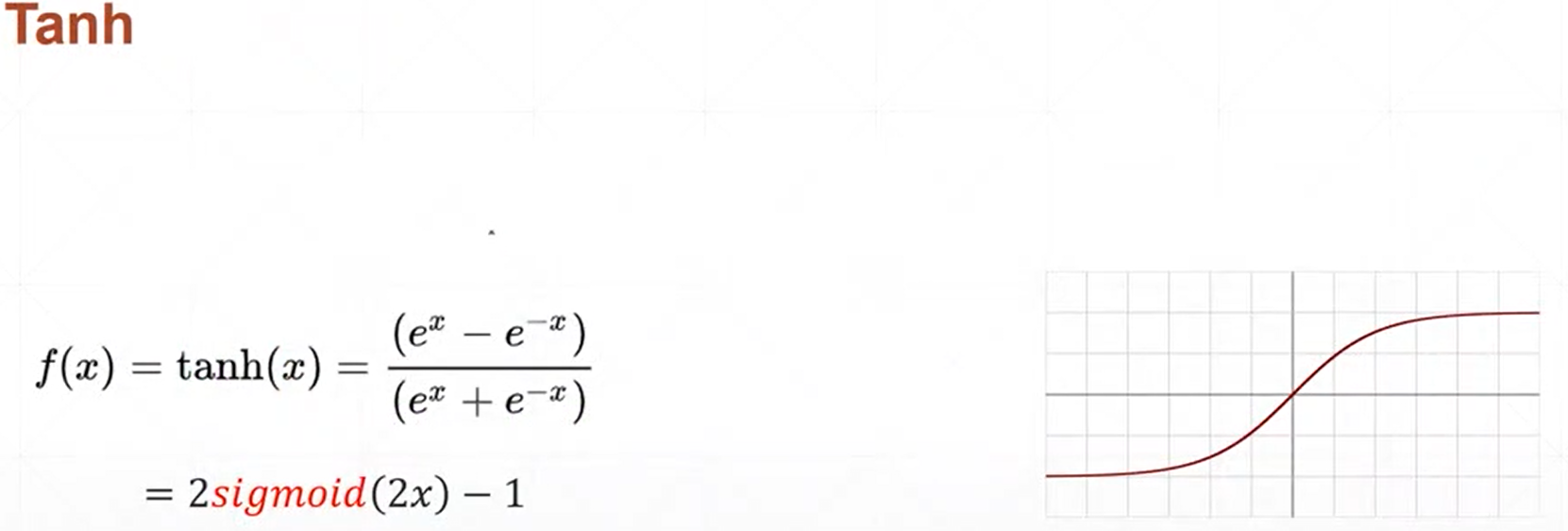
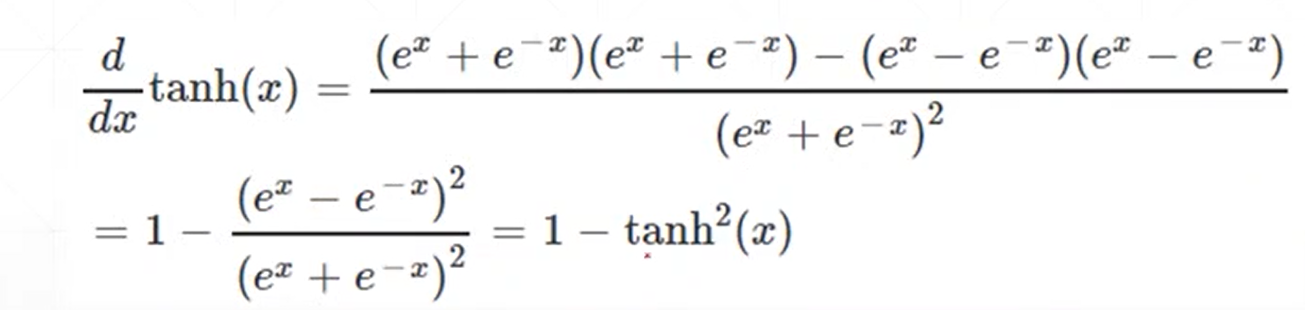
(3)Relu函数

6、常用的损失函数-loss函数
(1)MSE-回归问题
(2)Cross entropy loss-分类问题

7、对于MSE均方差的loss函数，计算时可以利用norm函数来进行计算，调用的格式如下所示：
MSE=torch.norm(y-y_pre,2).pow(2)
也可以直接调用API：
F.mse_loss(y,y_pre)来进行求解
8、对于梯度的求取在pytorch里面主要有两种方式：
(1)torch.autograd.grad(loss,[w0,w1,...],retain_graph=True)
(2)loss.backward(retain_graph=True) #其中使得retain_graph=True的目的是使得其不发生变化

图
9、感知机及其梯度推导——完整的神经网络的梯度计算的过程
(1)单输出模型的梯度计算

(2)多输出模型的梯度计算

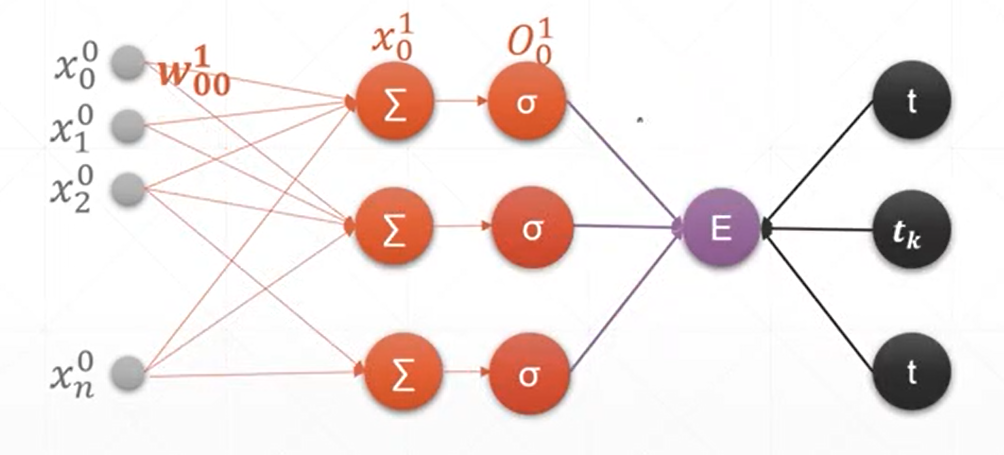
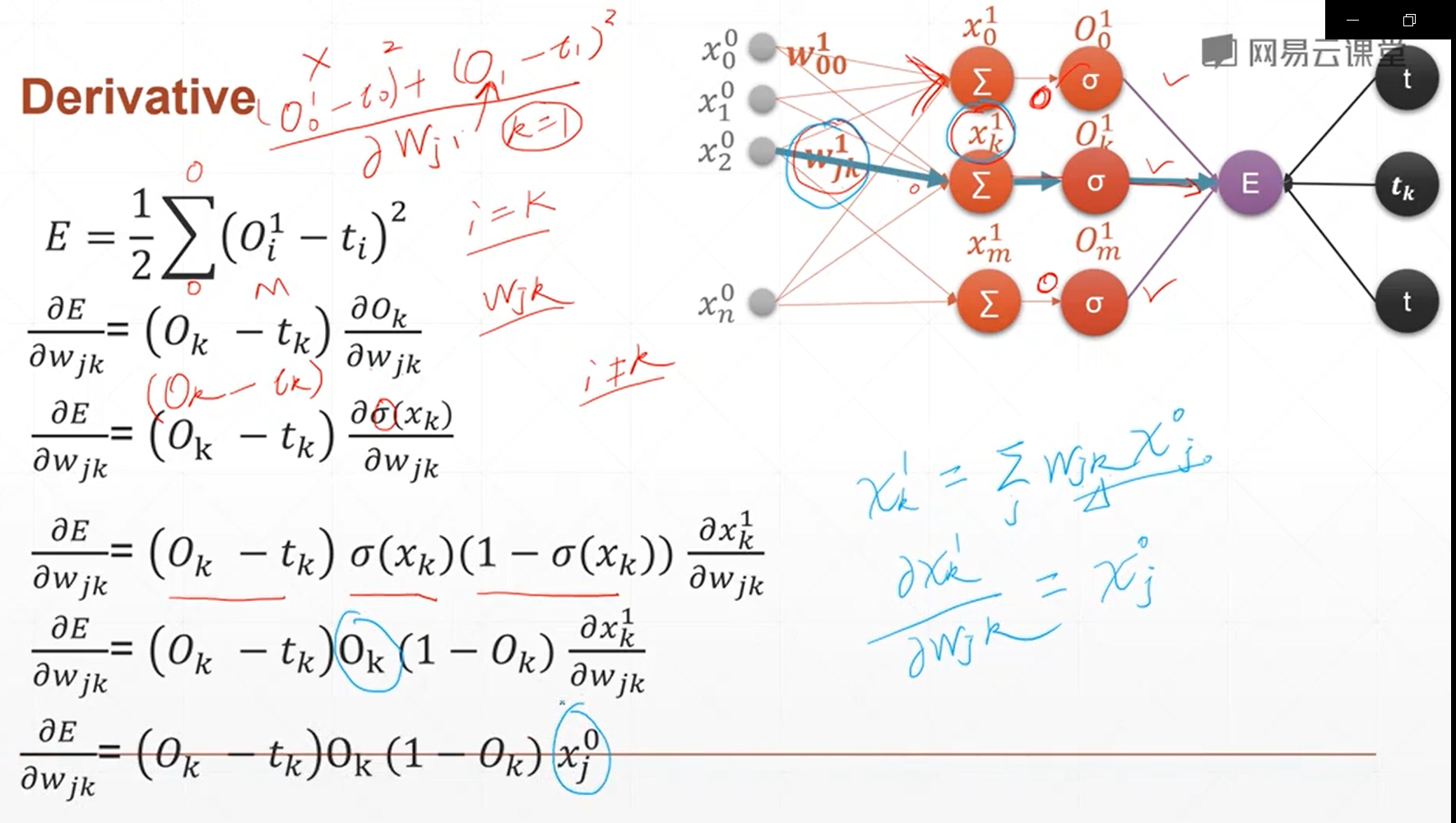
10、链式法则
链式法则主要是用来求取多隐含层和多输出的神经网络的梯度计算关系，它可以方便地进行计算，高效准确

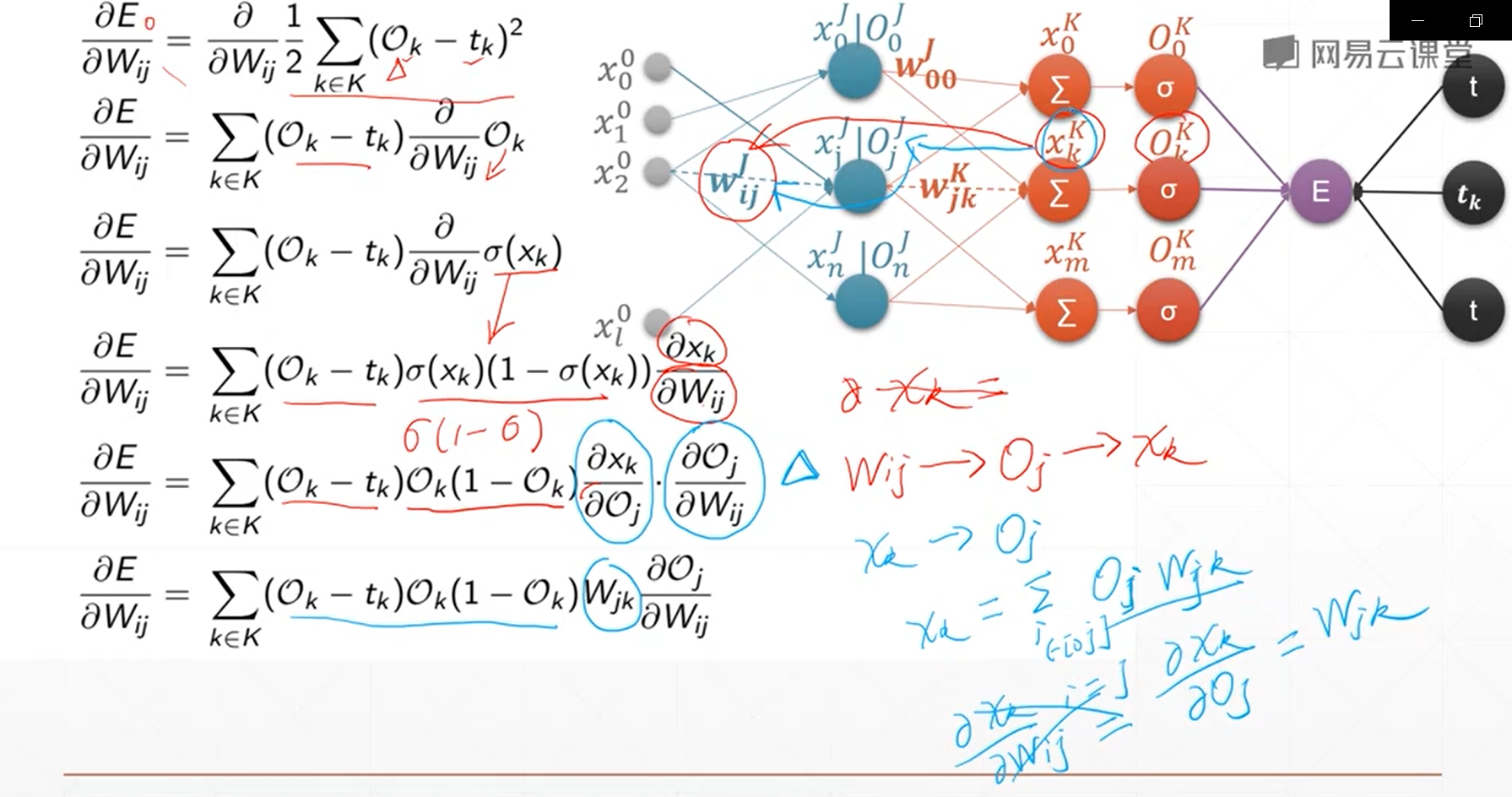
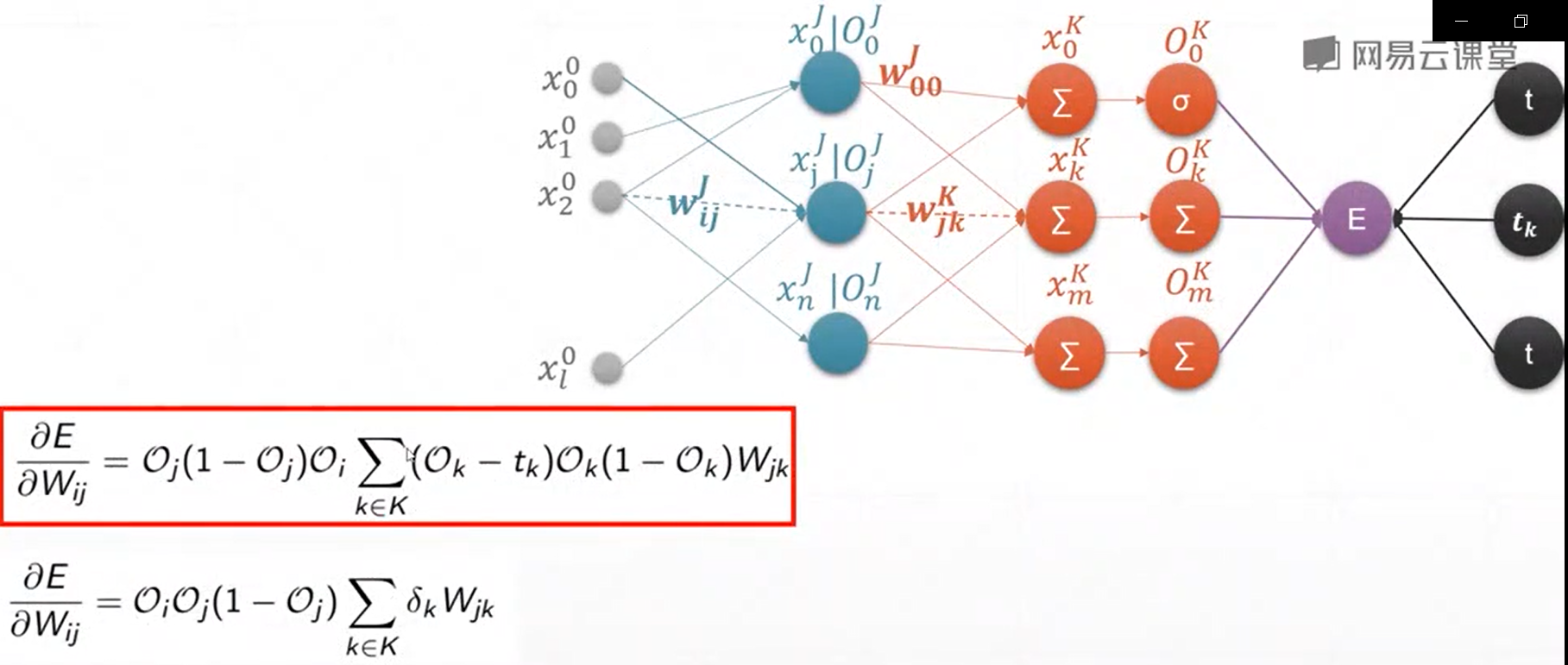
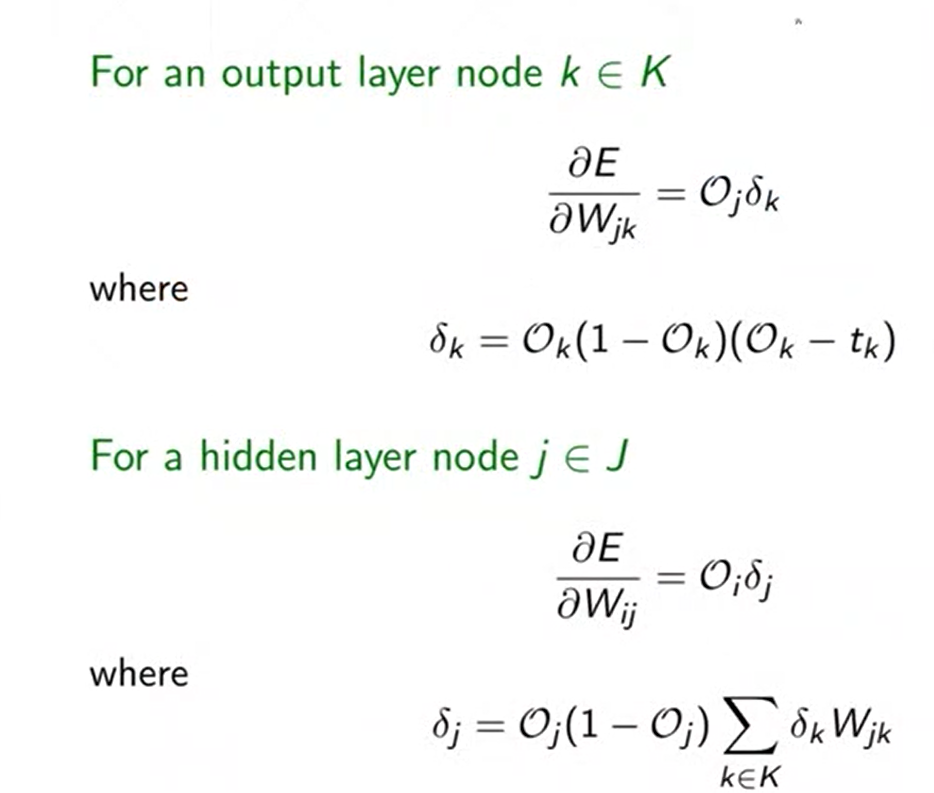
图
11、使用梯度下降法求解一个2D函数的最小值：
#反向传播过程解析
#2D函数最优化曲线
#画3D函数图像输出
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
import mpl_toolkits.mplot3d
figure=plt.figure()
#ax = Axes3D(figure)
ax=figure.gca(projection="3d")
x1=np.linspace(-6,6,1000)
y1=np.linspace(-6,6,1000)
x,y =np.meshgrid(x1,y1)
z=(x**2+y-11)**2+(x+y**2-7)**2
#ax.plot_surface(x,y,z,rstride=10,cstride=4,cmap=cm.YlGnBu_r)
ax.plot_surface(x,y,z,cmap="rainbow")
plt.show()

#梯度下降法寻找2D函数最优值函数
def f(x):
return (x[0]**2+x[1]-11)**2+(x[0]+x[1]**2-7)**2
x=torch.tensor([-4.,0.],requires_grad=True) #
optimizer=torch.optim.Adam([x],lr=1e-3)
for step in range(20000):
　　pre=f(x)
　　optimizer.zero_grad()
　　pre.backward()
　　optimizer.step()
　　if step % 2000==0:
　　　　print(step,x.tolist(),pre)

输出结果如下所示：