python数据结构与算法之问题求解实例

关于问题求解，书中有一个实际的案例。

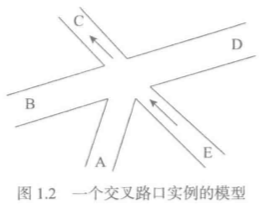
上图是一个交叉路口的模型，现在问题是，怎么安排红绿灯才可以保证相应的行驶路线互不交错。

第一步，就是把问题弄清楚。

怎么能让每一条行驶路线不冲突呢？

其实，就是给所有的行驶路线分组(这样保证了安全问题，不会撞车)。

并且，所做的分组应该尽可能大一些，用以提高路口的通行效率(经济问题，如果一个组一条路线，虽然不会撞车，但是等待的时间会很长)。

有了上面的最大化分组的想法。那么就进一步将问题具体化。

这个路口有13个可供行驶的方向：AB,AC,AD,BA,BC,BD,DA,DB,DC,EA,EB,EC,ED。

现在问题就转化为，给这13条路线分组，使其各个组不冲突，并且最大化组中的成员。

在书中引出了一个冲突图，用来表示各个路线的冲突。

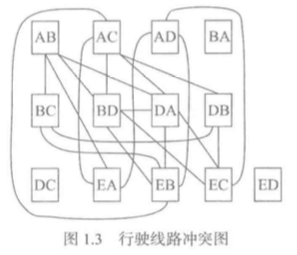
其中图中元素称之为顶点，连线称之为边或者弧。相互之间有边的顶点称为邻接顶点。

安全分组就变成了另外一种说法，为冲突图中的顶点确定一种分组，保证属于同一分组的所有顶点互不邻接。

到了这里就完了第一步，将问题严格化。

第二步，就是进行数据结构与算法设计

使用什么样的数据结构来表示冲突中的形式路线，又用哪种算法来计算分组。

书中首先提到了一个最佳着色算法，其实就是著名的四色问题，这个算法能找到最佳的分组方案。但是由于算法代价太高，效率不高。因此着重介绍了一个更为简单的算法。

那就是贪心法。它的基本想法是这样的：利用当时掌握的信息，尽可能地向得到解的方向前进，知道不能继续再换一个方法。

那么在这个例子中的具体表现就是：就是确定一个分组，这个分组里的成员互相都不邻接，也就是说不能冲突。当这个分组完成之后，再确定下一个分组。

按照这个方法，上面的例子分组就是：

{AB,AC,AD,BA,DC,ED}

{BC,BD,EA}

{DA,DB}

{EB,EC}

算法的伪代码如下：

输入：图G             #记录着图中顶点连接的关系

集合verts保存G中所有的顶点      #建立初始状态

设置集合groups为空集     #记录得到的分组，元素是顶点集合

while 存在未着色顶点：

　　选一种新的颜色

　　在未着色顶点中给尽量多的无连边的点着色(构建一个分组)

　　记录新着色的顶点组

python伪代码：

new_group = 空集

for v in verts：

　　if v 与new_group集合中的顶点都不相连：

　　　　将v从verts中取出

　　　　new_group.add(v)

循环结束时，new_grouo是可以用一种新的颜色着色的顶点集合

第三步，编写代码。

其实，上面的伪代码已经接近于具体程序了。只是还有一些细节需要考虑。

1、如何表示颜色。这个简单，用整数就可以。其实，用不用颜色表示都可以，只要将每个分组分开即可。这里采用二元组来表示，一个表示颜色，一个表示分好的组。、

2、如何记录分组。可以用一个集合来记录，也就是groups是集合的集合。

3、如何表示图结构？这个比较难，是后面的内容，这里先略过。

由此可得出python的代码：

def coloring(G)

　　color = 0

　　groups = set()

　　verts = vertices(G) #用来获取所有的顶点

　　while verts:

　　　　new_groups = set()

　　　　for v in list(verts):

　　　　　　if not_adjacent_with_set(v, newgroup, G):

　　　　　　　　new_group.add(v)

　　　　　　　　verts.remove(v)

　　　　groups.add((color, new_group))

　　　　color += 1

　　return grous

第四步，测试代码，寻找一些边界例子测试代码的严谨性以及逻辑性。

由于，这里并不是一个完整的项目，而且这个例子比较简单，就简单分析讨论一下，应该注意的几个问题。

1、它的解唯一吗？

其实，大致观察一下，就会发现，上面的算法只能给出一个恰好的解。例如，下面的分组也是一个解

{AB,EB,EC}

{AC,AD,BC,}

{BA,BD,DB,ED}

{DA,DC,EA}

其实，经过分析。对于BA、DC、ED三个顶点，将它们放在任何一个分组都是可以的。因为它们不跟任何一个顶点相连，也就是公认的无害右转弯。对于这个设计具体得看对于冲突概念的定义。

2、再次回顾一下算法的实现跟原来的问题是否相符

原来的问题是怎么分配，各个路线才能不冲突。

而上面的算法给出了一种不冲突的方法，但并不是最优的解。比如：上面的算法中每个分组都顶点都不允许重复，也就是各个分组互不相交。但真正的问题并没有这个要求。无害的右转弯就与各个分组都不冲突，完全可以都分配在各个分组里面。使其得到下面的分配：

{AB,AC,AD,BA,DC,ED}

{BC,BD,EA,BA,DC,ED}

{DA,DB,BA,DC,ED}

{EB,EC,BA,DC,ED}

这样就会将分组尽可能地扩充，使其经济效率更高(这个分组还可以继续扩充为{DA,DB,BA,DC,ED,AD})。

当然，这个问题还会有其他的一些具体的问题，这里就不讨论了。作者主要是用一个例子来带我们分析了一下，如何将生活中的实际问题，一步一步通过分析设计，最终得到一个完整的正确的效率高的计算机程序。