排序算法<No.4>【基数排序】

由于春节，以及项目要上线的原因，导致这期的算法博文跟进的有点慢，内疚！

今天要介绍的是排序算法中的基数排序（Radix Sort），这类排序也是一个分而治之的排序，是对桶排序的一个升级和改造，也是稳定的排序。

先来说下，什么是基数排序，这里重点要理解的是【基数】这个概念，什么是基数？

说到这个，举个简单而形象的例子，比如，我们说的十进制数，是按照10为基数的典范，这里的10就是基数。分为个位，十位，百位，千位......

另外，我们常常在娱乐中用到的扑克牌，也是可以进行排序的，它有两个维度，一个是数字点数，从A到K一共13个点，这个13就是基数；另外，还可以按花色排序，分为4种：红桃，梅花，黑桃，方片。

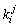概括而言，基数的选择和带排序的数据rd[n]的元素有关。这其中的元素rd[i]都由d个因子组成：，而这当中(0≤j<d)只不过是元素中的一个因子(如字符串、十进制整数等)。基数排序，则分为多因子基数排序和单因子基数排序。多因子排序中的每个因子的取值范围往往不同，比如扑克牌是两因子排序（花色，点数），而十进制整数排序，则是单因子基数排序。

设单因子的每个分量的取值范围均是：

C0≤kj≤Crd-1(0≤j<d)

可能的取值个数 rd 称为基数。

举例子概述下，方便理解：

(1) 若关键字是十进制整数，则按个、十等位进行分解，基数 rd=10，C0=0，C9=9，d 为最长整数的位数；

(2) 若关键字是小写的英文字符串，则 rd=26，Co='a'，C25='z'，d 为字符串的最大长度。

基数排序的基本思想：

将待排序的n个元素K(其中，元素的位序用j=d-1，d-2，…，0表示)，每个元素按照从低位到高位的顺序（LSD模式），分别对每个元素基于Kj（即元素的第j位大小）进行分组放入到对应的桶中。经过d轮桶排序后，n个元素就是有序的了。

基数排序的实现步骤：

1. 对待排序的n个元素进行特征分析，确定是单因子基数排序还是多因子基数排序。

2. 基于元素特征，找到基数rd。

3. 找到待排序元素中位数最多的因子，其长度d，决定要经过几轮桶排序，原始数据才有序。

4. 从最低位开始向高位（LSD）推进，对n个元素中的每一个，基于第j个因子，放入rd个桶中对应序号的一个。

5. 对rd个桶进行一次桶排序。

6. 重复4,5步骤，直到d轮桶排序结束。

上述的实现步骤，描述的已经很清楚。为了进一步将基数排序的思想描述清楚，下面，将结合一个具体的例子及代码实现，让读者更清楚的了解基数排序的真谛。

例子：

请用基数排序的思想，将下面的整数数列进行排序。

103,202,90,78,13,31,46,57,70,3,24

具体的java实现代码如下：

/**
 * @author "shihuc"
 * @date   2017年2月22日
 */
package radixSort;

import java.io.File;
import java.io.FileNotFoundException;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Scanner;

/**
 *
 * 定义辅助类，用来记录待排序的元素的值以及该值所占据的位数。
 *
 */
class Elem {
    int data;
    int length;
    /**
     * @return the data
     */
    public int getData() {
        return data;
    }
    /**
     * @return the length
     */
    public int getLength() {
        return length;
    }
    /**
     * @param data the data to set
     */
    public void setData(int data) {
        this.data = data;
    }
    /**
     * @param length the length to set
     */
    public void setLength(int length) {
        this.length = length;
    }
}
public class RadixSort {

    /**
     * @param args
     */
    public static void main(String[] args) {
        File file = new File("./src/radixSort/sample.txt");
        Scanner sc = null;
        try {
            sc = new Scanner(file);
            //获取测试例的个数
            int T = sc.nextInt();
            for(int i=0; i<T; i++){
                int MAX = 0;
                //获取每个测试例的元素个数
                int N = sc.nextInt();
                /*
                 * （2）获取基数rd。这里基数rd是预先指定的
                 */
                int rd = sc.nextInt();
                Elem A[] = new Elem[N];
                for(int j=0; j<N; j++){
                    int e = sc.nextInt();
                    int len = getElementLength(e, rd);
                    A[j] = new Elem();
                    A[j].setData(e);
                    A[j].setLength(len);
                    /*
                     * （3）下面获取MAX的过程，对应基数排序实现步骤中的第3步,即获取待排序数据的最大宽度（位数）
                     */
                    if(MAX < len){
                        MAX = len;
                    }
                }
                radixSort(A, rd, MAX);
                printResult(i, A);
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            if(sc != null){
                sc.close();
            }
        }
    }

    /**
     * 获取元素的长度
     *
     * @param ele 待排序的某一个元素
     * @param rd 基数值
     * @return ele的宽度（位数）
     */
    private static int getElementLength(int ele, int rd) {
        int len = 1;
        while(ele / rd > 0){
            len++;
            ele = ele / rd;
        }
        return len;
    }

    /**
     * 获取待排序元素的第currPos+1位的值 （从低位到高位序）
     *
     * @param ele 待排序的元素
     * @param rd 基数
     * @param length ele的宽度（位数）
     * @param curPos 当前处理的是第几位
     * @return 下一位对应的子元素
     */
    private static int getSubElem(int ele, int rd, int length, int curPos) {
        int subm = 0;

        while(ele / rd > 0 && subm <= curPos) {
            subm++;
            ele = ele / rd;
        }
        if(ele == 0 && subm <= curPos) {
            return -1;
        }else {
            if(ele == 0) {
                return 0;
            }else if(ele > 0 && subm > curPos) {
                return ele % rd;
            }
        }
        return -1;
    }

    /**
     * 基数排序的实现过程。
     *
     * @param src 待排序的数组
     * @param rd 基数
     * @param max 待排序数组元素的最大宽度（位数）
     */
    private static void radixSort(Elem src[], int rd, int max){
        /*
         * 对待排序元素进行max轮桶排序。 for循环实现这个逻辑。 对应基数排序实现步骤中的第（6）步
         */
        for(int i=0; i<max; i++){
            //定义rd个桶的map结构, 其中map的key表示rd的可能取值，value部分的ArrayList用来存放对应于基数范围内的某个值对应的待排序的元素
            HashMap<Integer, ArrayList<Elem>> buckets = new HashMap<Integer, ArrayList<Elem>>();
            /*
             * （4）下面的for循环，对应基数排序步骤中的第（4）步
             */
            for(int j=0; j<src.length; j++){
                int subm = getSubElem(src[j].getData(), rd, src[j].getLength(), i-1);
                //当当前待处理的基数元素的值Cj不存在，即待处理的待排序元素src[j]的值data位数不够，用0代替，放入0号桶。
                if(subm < 0){
                    subm = 0;
                }
                ArrayList<Elem> bucket = buckets.get(subm);
                if(bucket == null) {
                    bucket = new ArrayList<Elem>();
                    buckets.put(subm, bucket);
                }
                bucket.add(src[j]);
            }

            int stPos = 0;
            /*
             * 对桶内的数据采取快速排序,并将排序后的结果映射到原始数组中作为输出。对应基数排序实现步骤中的第（5）步
             */
            for(int bId = 0; bId < rd; bId++){
                ArrayList<Elem> bk = buckets.get(bId);
                //当某个基数范围内的元素值不存在时，则桶是不存在的，跳过。
                if(bk == null){
                    continue;
                }
                Elem[] org = new Elem[bk.size()];
                bk.toArray(org);
                quickSort(org, 0, bk.size() - 1);
                //将排序后的数据映射到原始数组中作为输出
                for(int n=0; n<org.length; n++){
                    src[stPos++] = org[n];
                }
            }
        }
    }

    /**
     * 采用类似两边夹逼的方式，向输入数组的中间某个位置夹逼，将原输入数组进行分割成两部分，左边的部分全都小于某个值，
     * 右边的部分全都大于某个值。
     *
     * 快排算法的核心部分。
     *
     * @param src 待排序数组
     * @param start 数组的起点索引
     * @param end 数组的终点索引
     * @return 中值索引
     */
    private static int middle(Elem src[], int start, int end){
        int middleValue = src[start].getData();
        Elem mv = src[start];
        while(start < end){
            //找到右半部分都比middleValue大的分界点
            while(src[end].getData() >= middleValue && start < end){
                end--;
            }
            //当遇到比middleValue小的时候或者start不再小于end，将比较的起点值替换为新的最小值起点
            src[start] = src[end];
            //找到左半部分都比middleValue小的分界点
            while(src[start].getData() <= middleValue && start < end){
                start++;
            }
            //当遇到比middleValue大的时候或者start不再小于end，将比较的起点值替换为新的终值起点
            src[end] = src[start];
        }
        //当找到了分界点后，将比较的中值进行交换，将中值放在start与end之间的分界点上，完成一次对原数组分解，左边都小于middleValue，右边都大于middleValue
        src[start] = mv;
        return start;
    }

    /**
     * 通过递归的方式，对原始输入数组，进行快速排序。
     *
     * @param src 待排序的数组
     * @param st 数组的起点索引
     * @param nd 数组的终点索引
     */
    public static void quickSort(Elem src[], int st, int nd){

        if(st > nd){
            return;
        }
        int middleIdx = middle(src, st, nd);
        //将分隔后的数组左边部分进行快排
        quickSort(src, st, middleIdx - 1);
        //将分隔后的数组右半部分进行快排
        quickSort(src, middleIdx + 1, nd);
    }

    /**
     * 打印最终的输出结果
     *
     * @param idx 测试例的编号
     * @param B 待输出数组
     */
    private static void printResult(int idx, Elem B[]){
        System.out.print(idx + "--> ");
        for(int i=0; i<B.length; i++){
            System.out.print(B[i].getData() + "  ");
        }
        System.out.println();
    }

}

下面附上测试例数据，即sample.txt的内容：

3
11 10
103 202 90 78 13 31 46 57 70 3 24
11 10
24 3 70 57 46 31 13 78 90 202 103
18 10
99 290 87 17 1032 22219 2 13 32 33 219 88 76 85 2017 1982 10 2015

其中，第一组测试例数据，就是本博文中的例题待排序数据。

下面附上测试例对应的结果：

0--> 3  13  24  31  46  57  70  78  90  103  202
1--> 3  13  24  31  46  57  70  78  90  103  202
2--> 2  10  13  17  32  33  76  85  87  88  99  219  290  1032  1982  2015  2017  22219

代码源码中，红色部分，分别指出对应的实现步骤中的第几步，其中，代码中没有反应出实现步骤的第一步，其实这第一步往往是问题思考过程中确定算法方案时，定义的。第一步会影响到后面几步的具体实施细节。

【说明】： 本代码实现，处理的数据，只能是非负数，要想其也能支持负数，需要在基数选取上做下修改，比如将10改成20，相应的改动及实现，读者自己可以思考

基数排序的速度还是很快的，也是一种用空间换时间的策略，因为基数排序，要额外开辟rd（基数）个桶，而桶排序的每个子排序（对每个桶的排序）时间，是有些许不同的，依赖于子排序的算法，上述代码实现中，采用的是快速排序。

基数排序的时间是近乎线性的(请参照桶排序博文)。，基数排序所需的辅助存储空间为 O(n+rd)。