文本分类学习 （九）SVM入门之拉格朗日和KKT条件

上一篇说到SVM需要求出一个最小的||w|| 以得到最大的几何间隔。

求一个最小的||w|| 我们通常使用

来代替||w||,我们去求解 ||w||² 的最小值。然后在这里我们还忽略了一个条件，那就是约束条件，在上一篇的公式（8）中的不等式就是n维空间中数据点的约束条件。只有在满足这个条件下，求解||w||²的最小值才是有意义的。思考一下，若没有约束条件，那么||w||²的最小值就是0，反应在图中就是H₁和H₂的距离无限大那么所有点都会在二者之间，都属于同一类，而无法分开了。

求最小值的目标函数和约束条件s.t.

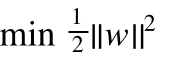
    （1）

x_i和y_i分别表示样本向量和样本所属的标签，w 是自变量，本身是一个向量。

求最小值也就是求最优值，它有一个很好听的名字叫做规划，而我们的目标函数是1/2 * ||w||²是一个二次函数，二次函数属于凸函数，所以改求解也就有个更好听的名字叫做凸二次规划 

对于这种带有约束条件的规划问题，我们可以通过一定的方式把约束条件去掉！

凸函数和凸集

这里提一下凸函数，提到凸函数就要提交凸集或者凸包，凸集内的如意两个点的连线，都在凸集之内。满足这样的集合就叫凸集，比如正方形，六边形都是凸集。

那么凸函数：对区间[a,b]上定义的函数f，若它对区间中任意两点x1,x2均有：

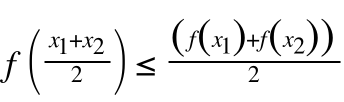      （2）

 

则称f为区间[a,b]上的凸函数。

引入拉格朗日乘数，来消除约束条件

拉格朗日乘子法：

对于 带约束的优化问题：

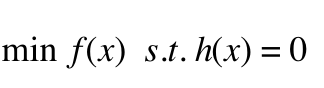　　    （3）

则可以通过拉格朗日乘子构造拉格朗日函数

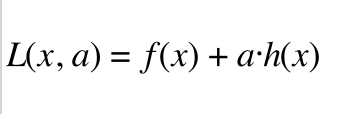     （4）

其中a是一个拉格朗日乘子构成的向量（a₁,a₂,a₃,a₄,....）ai>0

然后在对x 和 拉格朗日乘子a 求导，连立方程求出x 和 a ,再把x代入目标函数中求得极值.

回到我们的问题，通过拉格朗日乘子法构建拉格朗日函数, 在此之前我们把约束条件左边加上负号，让其条件变成小于0

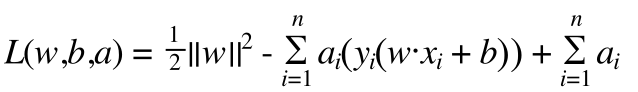 （5）

我们设

            （6）

如果x_i满足约束条件，y_i(w * x_i + b) >= 1，则 θ_p(x)要取最大值，只能让 α= 0 就是取0向量，则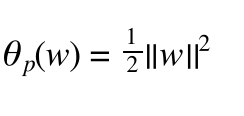
         （7）

如果x_i不满足条件 y_i(w * x_i + b) <= 1 要取最大值，那么α 可以无限大，所有

             （8）

所以我们看以看出 θ_p(x) 已经实现了把约束条件变成无约束条件

所以（1）中的带有约束条件的目标函数，就可以变成求（6）式（不带约束）的最小值，原因就是上面（7）和（8）公式 :

     （9）

我们直接求解此比较困难，需要这个式子转换成它的对偶问题（min 和 max 调换位置），再去求解这个对偶问题：

               （10）

为什么可以通过转换成对偶问题来求解原问题呢？因为存在这样一条定理设原问题的解为p* 它的对偶问题解为d*,一般情况下有d*<=p*, 证明过程就不写了。

所以求解对偶问题只能得到原问题解的下界，而不能保证d* = p*。

对这个对偶问题进行求解，先求min_w,bL(w,b,a) 把a 当做常数 对w 和 b分别求导可以得到：

        (11)

               (12)

把（11）和（12）式代入 （5）式中可以求得min_w,bL(w,b,a)

（13）

可以看到（13）式中的w 和 b都消失了，（13）式是min_w,bL(w,b,a)的值，求完最小值，还要求max_ai>0

  (14)

如果把（14）问题中的 a 求出来，那么w 也就能求出来（通过（11）），b 也就可以求出了。

先不管怎么把a 求出来，因为这里有很多算法可以去求解，用的最多的就是SMO算法。

我们接下来证明这个通过对偶问题求出来的解 d* 就是我们想要的原问题解 p* ,这里就要介绍到KKT条件

根据（11）和 （12）式，我们可以得出

再根据原问题中的约束条件，我们可以得出

这5个条件加起来就满足了KKT条件，KKT条件是对偶问题的解d* = p* 的充分必要条件

以下是证明过程：