HDU 5852 Intersection is not allowed!（LGV定理行列式求组合数）题解

题意：有K个棋子在一个大小为N×N的棋盘。一开始，它们都在棋盘的顶端，它们起始的位置是 (1,a1),(1,a2),...,(1,ak) ，它们的目的地是 (n,b1),(n,b2),...,(n,bk)。

一个位于 (r,c) 的棋子每一步只能向右走到 (r,c+1) 或者向下走到 (r+1,c) 。

我们把 i 棋子从 (1,ai) 走到 (n,bi) 的路径记作 pi 。

你的任务是计算有多少种方案把n个棋子送到目的地，并且对于任意两个不同的棋子 i,j ，使得路径 pi 与 pj 不相交（即没有公共点）。

思路：这里有一个结论，n个起点到n个终点的不相交路径的种数为：每个起点到每个终点的可能数组成的n*n的矩阵的行列式。

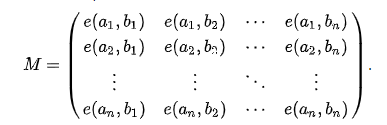
即求上矩阵行列式，其中e（ai，bi）代表从ai起点到bi终点的可能路径数量。

行列式求解用高斯消元。提交要用G++，C++一直超时emmmm

参考：HDU 5852：Intersection is not allowed!（行列式+逆元求组合数）

代码:

#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const int maxn = 1e5 + ;
const int seed = ;
const ll MOD = ;
const int INF = 0x3f3f3f3f;
int a[maxn], b[maxn];
ll e[][];
ll fac[maxn << ], niYuan[maxn << ];
ll pmul(ll a, ll b){
    ll ans = ;
    while(b){
        if(b & ) ans = ans * a % MOD;
        a = a * a % MOD;
        b >>= ;
    }
    return ans;
}
ll C(int n, int m){
    ll ret = fac[n] * niYuan[m] % MOD;
    return ret * niYuan[n - m] % MOD;
}
void initFac(){
    fac[] = niYuan[] = ;
    for(ll i = ; i <= ; i++){
        fac[i] = fac[i - ] * i % MOD;
        niYuan[i] = pmul(fac[i], MOD - );
    }
}
ll guass(int n){
    ll ans = , f = ;  //行列式和符号位
    for(int i = ; i <= n; i++){
        for(int j = i + ; j <= n; j++){
            int x = i, y = j;
            while(e[y][i]){
                ll t = e[x][i] / e[y][i];
                for(int k = i; k <= n; k++)
                    e[x][k] = (e[x][k] - e[y][k] * 1LL * t % MOD) % MOD;
                swap(x,y);
            }
            if(x != i){
                for(int k = ; k <= n; k++)
                    swap(e[i][k], e[j][k]);
                f = -f;
            }
        }
        ans = ans * e[i][i] % MOD;
        if(ans == ) return ;
    }
    return (ans * f + MOD) % MOD;
}
int main(){
    initFac();
    int t;
    scanf("%d", &t);
    while(t--){
        int n, k;
        scanf("%d%d", &n, &k);
        for(int i = ; i <= k; i++)
            scanf("%d", &a[i]);
        for(int i = ; i <= k; i++)
            scanf("%d", &b[i]);
        for(int i = ; i <= k; i++){
            for(int j = ; j <= k; j++){
                if(b[j] >= a[i]){
                    e[i][j] = C(n -  + b[j] - a[i], b[j] - a[i]);
                }
                else e[i][j] = ;
            }
        }
        printf("%lld\n", guass(k));
    }
    return ;
}