RRT路径规划算法（matlab实现）

基于快速扩展随机树（RRT / rapidly exploring random tree）的路径规划算法，通过对状态空间中的采样点进行碰撞检测，避免了对空间的建模，能够有效地解决高维空间和复杂约束的路径规划问题。该方法的特点是能够快速有效地搜索高维空间，通过状态空间的随机采样点，把搜索导向空白区域，从而寻找到一条从起始点到目标点的规划路径，适合解决多自由度机器人在复杂环境下和动态环境中的路径规划。与PRM类似，该方法是概率完备且不最优的。

RRT是一种多维空间中有效率的规划方法。它以一个初始点作为根节点，通过随机采样增加叶子节点的方式，生成一个随机扩展树，当随机树中的叶子节点包含了目标点或进入了目标区域，便可以在随机树中找到一条由从初始点到目标点的路径。基本RRT算法如下面伪代码所示：

function feasible=collisionChecking(startPose,goalPose,map)%冲突检查：判断起始点到终点之间是否有障碍物

feasible=true;%可行的，可执行的
dir=atan2(goalPose(1)-startPose(1),goalPose(2)-startPose(2));%目标点和起始点之间的角度
for r=0:0.5:sqrt(sum((startPose-goalPose).^2))%sqrt(sum((startPose-goalPose).^2)):两点间的距离
    posCheck = startPose + r.*[sin(dir) cos(dir)];%以0.5的间隔得到中间的点
    if ~(feasiblePoint(ceil(posCheck),map) && feasiblePoint(floor(posCheck),map) && ...
            feasiblePoint([ceil(posCheck(1)) floor(posCheck(2))],map) && feasiblePoint([floor(posCheck(1)) ceil(posCheck(2))],map))
        feasible=false;break;
    end
    if ~feasiblePoint([floor(goalPose(1)),ceil(goalPose(2))],map), feasible=false; end

end

function feasible=feasiblePoint(point,map)%判断点是否在地图内，且没有障碍物
feasible=true;
if ~(point(1)>=1 &&  point(1)<=size(map,1) && point(2)>=1 && point(2)<=size(map,2) && map(point(2),point(1))==255)%map(point(2),point(1))==255：没有障碍物
    feasible=false;
end

function distance=Distance(start_Pt,goal_Pt)
distance=sqrt((start_Pt(1)-goal_Pt(1))^2+(start_Pt(2)-goal_Pt(2))^2);

function [X_near,index]=Near(X_rand,T)
min_distance=sqrt((X_rand(1)-T.v(1).x)^2+(X_rand(2)-T.v(1).y)^2);
for T_iter=1:size(T.v,2)
    temp_distance=sqrt((X_rand(1)-T.v(T_iter).x)^2+(X_rand(2)-T.v(T_iter).y)^2);
    if temp_distance<=min_distance
        min_distance=temp_distance;
        X_near(1)=T.v(T_iter).x
        X_near(2)=T.v(T_iter).y
        index=T_iter;
    end
end

function X_rand=Sample(map,goal)
% if rand<0.5
%     X_rand = rand(1,2) .* size(map);   % random sample
% else
%     X_rand=goal;
% end

if unifrnd(0,1)<0.5
   X_rand(1)= unifrnd(0,1)* size(map,1);   % 均匀采样
   X_rand(2)= unifrnd(0,1)* size(map,2);   % random sample
else
   X_rand=goal;
end

function X_new=Steer(X_rand,X_near,StepSize)
theta = atan2(X_rand(1)-X_near(1),X_rand(2)-X_near(2));  % direction to extend sample to produce new node
X_new = X_near(1:2) + StepSize * [sin(theta)  cos(theta)];

% dir_x = X_rand(1)- X_near(1);
% dir_y = X_rand(2)- X_near(2);
% dir = sqrt(dir_x^2 + dir_y^2);
% X_new(1) = dir_x * StepSize/dir+X_near(1);
% X_new(2) = dir_y * StepSize/dir+X_near(2);

function X_rand=Sample(map,goal)
% if rand<0.5
%     X_rand = rand(1,2) .* size(map);   % random sample
% else
%     X_rand=goal;
% end

if unifrnd(0,1)<0.5
   X_rand(1)= unifrnd(0,1)* size(map,1);   % 均匀采样
   X_rand(2)= unifrnd(0,1)* size(map,2);   % random sample
else
   X_rand=goal;
end

%***************************************
%Author: Chenglong Qian
%Date: 2019-11-5
%***************************************
%% 流程初始化
clear all; close all;
x_I=1; y_I=1;           % 设置初始点
x_G=700; y_G=700;       % 设置目标点
goal(1)=x_G;
goal(2)=y_G;
Thr=50;                 %设置目标点阈值 当到这个范围内时则认为已到达目标点
Delta= 30;              % 设置扩展步长，扩展结点允许的最大距离
%% 建树初始化
T.v(1).x = x_I;         % T是我们要做的树，v是节点，这里先把起始点加入到T里面来
T.v(1).y = y_I;
T.v(1).xPrev = x_I;     % 起始节点的父节点仍然是其本身
T.v(1).yPrev = y_I;
T.v(1).dist=0;          %从父节点到该节点的距离，这里可取欧氏距离
T.v(1).indPrev = 0;     %父节点的索引
%% 开始构建树——作业部分
figure(1);
ImpRgb=imread('newmap.png');
Imp=rgb2gray(ImpRgb);
imshow(Imp)
xL=size(Imp,1);%地图x轴长度
yL=size(Imp,2);%地图y轴长度
hold on
plot(x_I, y_I, 'ro', 'MarkerSize',10, 'MarkerFaceColor','r');
plot(x_G, y_G, 'go', 'MarkerSize',10, 'MarkerFaceColor','g');% 绘制起点和目标点
count=1;
for iter = 1:3000
%     x_rand=[];
    %Step 1: 在地图中随机采样一个点x_rand
    %提示：用（x_rand(1),x_rand(2)）表示环境中采样点的坐标
    x_rand=Sample(Imp,goal);
%     x_near=[];
    %Step 2: 遍历树，从树中找到最近邻近点x_near
    %提示：x_near已经在树T里
    [x_near,index]= Near(x_rand,T);
    plot(x_near(1), x_near(2), 'go', 'MarkerSize',2);
%     x_new=[];
    %Step 3: 扩展得到x_new节点
    %提示：注意使用扩展步长Delta
    x_new=Steer(x_rand,x_near,Delta);
    %检查节点是否是collision-free
    if ~collisionChecking(x_near,x_new,Imp) %如果有障碍物则跳出
       continue;
    end
    count=count+1;

    %Step 4: 将x_new插入树T
    %提示：新节点x_new的父节点是x_near
    T.v(count).x = x_new(1);
    T.v(count).y = x_new(2);
    T.v(count).xPrev = x_near(1);     % 起始节点的父节点仍然是其本身
    T.v(count).yPrev = x_near(2);
    T.v(count).dist=Distance(x_new,x_near);          %从父节点到该节点的距离，这里可取欧氏距离
    T.v(count).indPrev = index;     %父节点的索引
    %Step 5:检查是否到达目标点附近
    %提示：注意使用目标点阈值Thr，若当前节点和终点的欧式距离小于Thr，则跳出当前for循环
    if Distance(x_new,goal) < Thr
        break;
    end
   %Step 6:将x_near和x_new之间的路径画出来
   %提示 1：使用plot绘制，因为要多次在同一张图上绘制线段，所以每次使用plot后需要接上hold on命令
   %提示 2：在判断终点条件弹出for循环前，记得把x_near和x_new之间的路径画出来
%    plot([x_near(1),x_near(2)],[x_new(1),x_new(2)]);
%    hold on
  line([x_near(1),x_new(1)],[x_near(2),x_new(2)]);
   pause(0.1); %暂停0.1s，使得RRT扩展过程容易观察
end
%% 路径已经找到，反向查询
if iter < 2000
    path.pos(1).x = x_G; path.pos(1).y = y_G;
    path.pos(2).x = T.v(end).x; path.pos(2).y = T.v(end).y;
    pathIndex = T.v(end).indPrev; % 终点加入路径
    j=0;
    while 1
        path.pos(j+3).x = T.v(pathIndex).x;
        path.pos(j+3).y = T.v(pathIndex).y;
        pathIndex = T.v(pathIndex).indPrev;
        if pathIndex == 1
            break
        end
        j=j+1;
    end  % 沿终点回溯到起点
    path.pos(end+1).x = x_I; path.pos(end).y = y_I; % 起点加入路径
    for j = 2:length(path.pos)
        plot([path.pos(j).x; path.pos(j-1).x;], [path.pos(j).y; path.pos(j-1).y], 'b', 'Linewidth', 3);
    end
else
    disp('Error, no path found!');
end

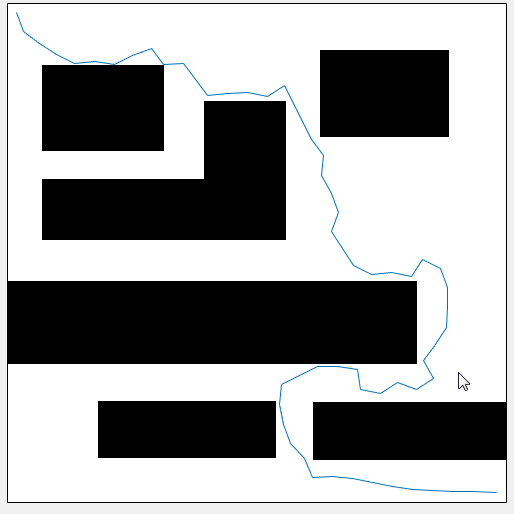
参考链接：https://www.cnblogs.com/flyinggod/p/8727951.html