背包&数位dp(8.7)

背包

0/1背包

设dp[i][j]为前i个物品选了j体积的物品的最大价值/方案数

dp[i][j]=max(dp[i-1][j-w[i]]+v[i],dp[i-1][j])(最大价值)

dp[i][j]=dp[i-1][j-w[i]]+dp[i-1][j](方案数)

输出方案：

dp[i][j]=max(dp[i-1][j-w[i]]+v[i],dp[i-1][j])

看方程，我们可以记录第i个物品选不选，如果选，再递归到dp[i-1][j-w[i]]即可

有价值的情况下记录最优策略方案数

①：dp[i-1][j]≠dp[i-1][j-w[i]]:dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]])

②：dp[i-1][j]==dp[i-1][j-w[i]]:dp[i][j]=dp[i-1][j]+dp[i-1][j-w[i]]

两种写法：

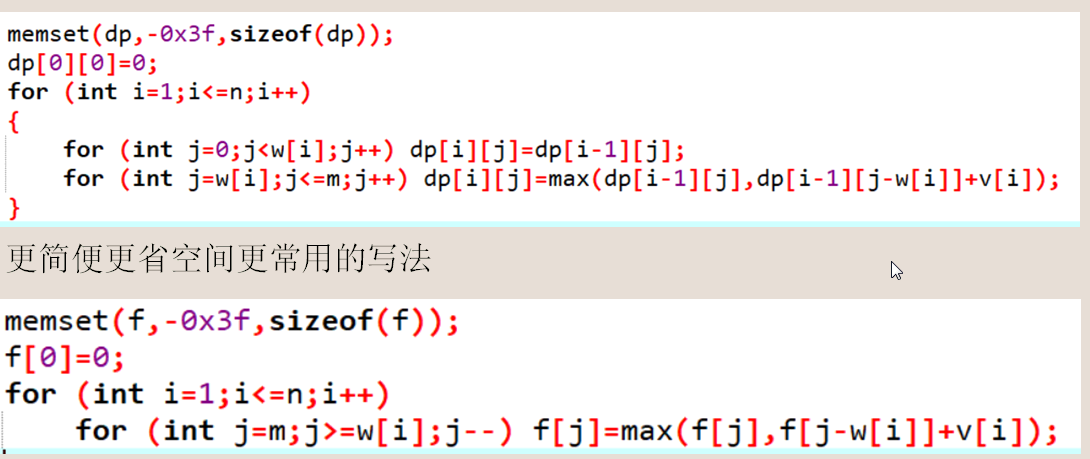
完全背包

多重背包

两种写法：

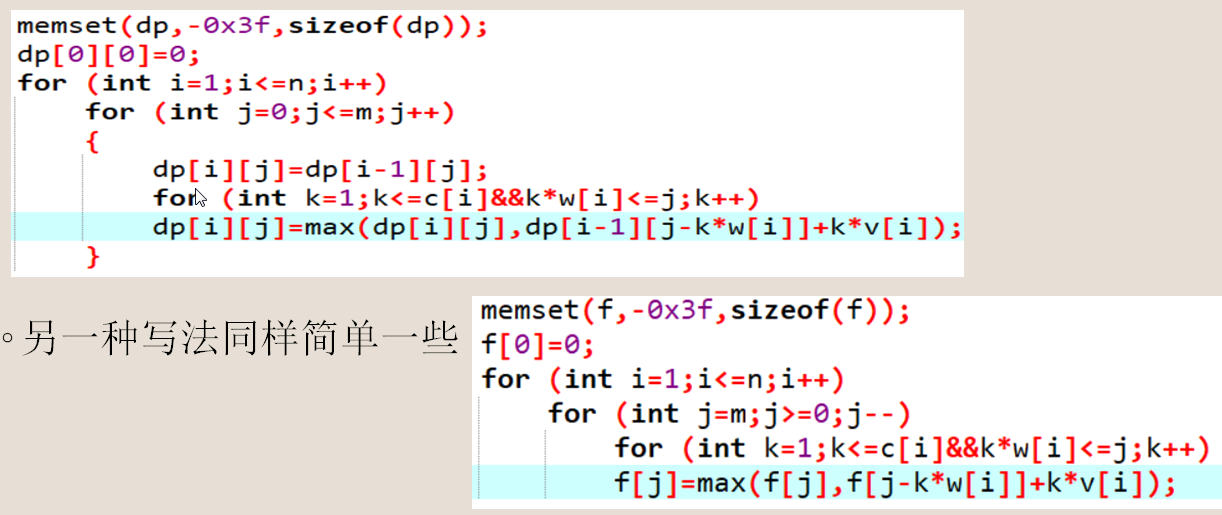
然后还有什么二进制优化是吧

就是把第i种物品按照t[i]的二进制拆分来打包

举个例子：t[i]=5，二进制：101

那就打成有四个物品的包和有一个物品的包

四个物品的包的体积是4*w[i],价值是4*v[i]

当t[i]不是2^m怎么办？

放心任何一个数都可以用二进制表示出来(就是进行一些特殊处理)

这样就可以拆成logt[i]个包

然后当0/1背包搞就好了

考虑一种物品的复杂度就是m*log(t[i])

从m*t优化成了m*log，海星海星

多重背包求方案数：

二进制优化还正确吗？

我们回去看看拆分方式，按照二进制拆分。当x=0时，木有问题。

但当x不为0时，多个选择的方案可能会拆出重复的东西来，就不行了

单调队列优化：

设f_r[i][j]=dp[i-1][j*w[i]+r]

什么鬼？

就是把x%w[i]==r的所有的dp[i-1][x]值提出来了

那么f_r[i][j]=max{f_r[i-1][j-k]+v[i]*k(0<=k<=t[i]}

这又是什么鬼？

我们枚举选的个数k,既然选了k,那之前应该有j-k个已经选了，再加上选的k个的权值

变形：fr[i][j]=max{fr[i-1][p]+v[i]*(j-p)}(j>=p>=j-t[i])（用p代替j-k）

继续：fr[i][j]=max{fr[i-1][p]-v[i]*p}+v[i]*j(j>=p>=j-t[i]) (就是把上面的v[i]*(j-p)拆开)

那么求最大值就只与p有关了

我们注意到j每次+1，那么p的最小值每次就+1。感觉像滑动窗口有木有。然后就是单调队列了ρωρ

zhx可以吗三连

所以单调队列在求方案数的时候可以吗？

单调队列不可以，但是思想可以。

为毛单调队列不可以呢？因为这里是求和啊求和（求方案数），直接前缀和不就好辣

分组背包

dp[i][j]表示前i组，选了j的体积的最大价值？？？

dp[i][j]=max{dp[i-1][j-w[i][k]]+v[i][k]}(k<=size[i])

就是枚举选哪个物品辣

经经经典题

二维完全背包（大概

dp[i][j]表示选了i体积的氧气，j体积的氢气的最大值

dp[i][j]=max{dp[i-a[k]][j-b[k]]+w[k]}(这里压缩了一维,把原来的前i个给扔了)

xLO₂,yLH₂,cLCl_{2,怎么办？再来一维}

vijos1240

据说最多只能有一对夫妻在一个房间里，其他都是全男/全女

证明：

默认每个房间的容量≥2（单身狗专用单间考虑考虑），如果有两对夫妻都单独住房，那么显然让男人住一起，女人住一起更优

dp[i][x][y]:前i个房间住了x个男人，y个女人

不考虑夫妻：dp[i][x][y]=min{dp[i-1][x-房间容量][y],dp[i-1][x][y-房间容量]}

考虑夫妻：

bzoj1190

n<=100

数据好大鸭

a比较小是唯一的特殊条件了

按照b从大到小排序，先处理b大的宝石

f[i][j]表示在二进制中到了第i位，剩下j*2ⁱ的重量可用，最大价值

因为当前考虑的i==b,所以b暂时木有用。f[i][j]+v[i]------>f[i+1][j-a_i]，a<=10,n<=100,所以最多记录到1000就完事了

接下来我们考虑转移到f[i-1][j'],那么j'=j*2+(W的第i-1位)

然后再和考虑f[i][j]时一样就好了

看看这询问数量，爽

我们回忆一下背包加上一个东西的复杂度是O(m)(就是辣个dp转移的for循环)

据说有个东西叫分治优化背包

我们搞一个函数dd(l,r)，表示原序列的区间[l,r]禁止购买时求最大价值

让我们画一画

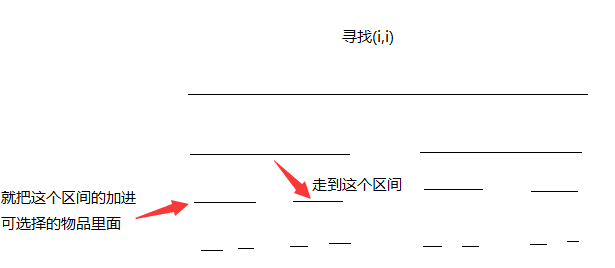
发现走左区间就把右区间加到可购买的背包里面，走右区间相反

这样dp(i,i)就是禁止购买i时的最大价值

f[j]表示选出一些物品（当前物品选），体积为j的方案数

g[j]表示当前物品i不选，体积为j的方案数

f[j]=f[j]+f[j-w[i]]

f[j]=g[j]+g[j-w[i]]

第二个式子是个什么鬼？

总方案数=不选的方案数+不选i装满j-w[i]的方案数（这样再选上i就可以装满j了）

所以g[j]=f[j]-g[j-w[i]],g从小到大枚举，即可求出答案

注意当0≤j<w[i]时，g[j]=f[j]

f[j]可能会很大，注意边求边取模

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<cmath>
using namespace std;
const int inf=;
typedef long long ll;
inline int read()
{
    char ch=getchar();
    int x=;bool f=;
    while(ch<''||ch>'')
    {
        if(ch=='-')f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return f?-x:x;
}
int w[],n,m,f[],g[];
int main()
{
    n=read();m=read();
    for(int i=;i<=n;i++)
     w[i]=read();
    f[]=;
    for(int i=;i<=n;i++)
     for(int j=m;j>=w[i];j--)
      f[j]+=f[j-w[i]],f[j]=(f[j]+)%; //千万记得取模！
    for(int i=;i<=n;i++)
    {
        for(int j=;j<w[i];j++)
         g[j]=f[j];
        for(int j=w[i];j<=m;j++)
        g[j]=(f[j]-g[j-w[i]]+)%;
        for(int j=;j<=m;j++)
         printf("%d",(g[j]+)%);
        printf("\n");
    }
}

总体积/2,看最接近的数

但是怎么求呢？

先看点别的

整数划分问题

是背包鸭

1.n是总体积，k是完全背包的容积

dp[i][j][x]:考虑1~i个数，选了j个数，和为x的方案数

更优一点

上述的分类方法：末尾是否有1

dp[i-1][j-1]:末尾有1，那就把1拿掉，剩下i-1,同时要划分出j-1个数

dp[i-j][j]:末尾没有1，那最后一列的高度就高于1，那么直接切掉一层，变成i-j划分成j列

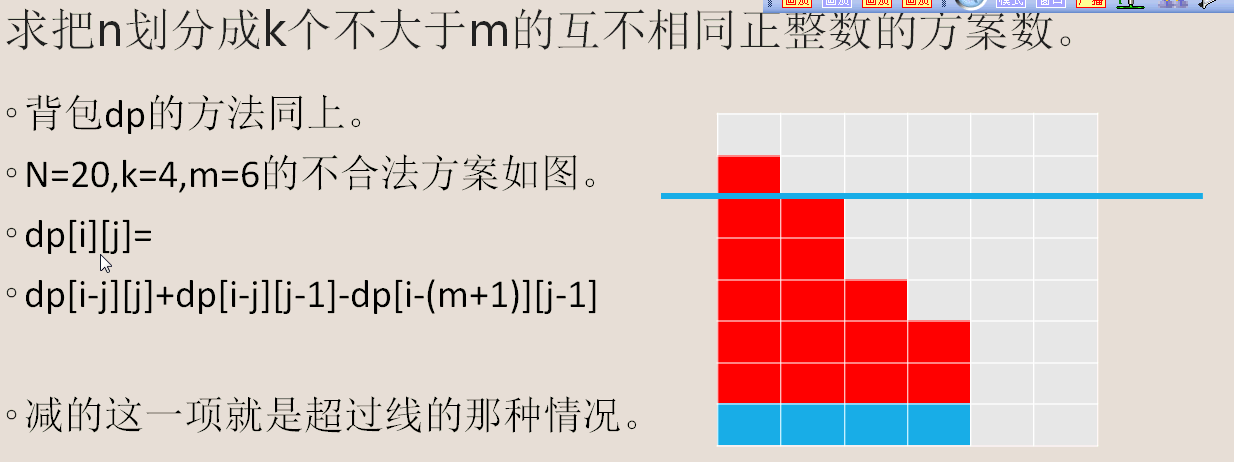
2.考虑1的思路，增加了一个互不相同的限制。

还是考虑是否末尾有1

有1：dp[i-j][j-1]，为什么是i-j呢？因为dp[i-1][j-1]中可能会有一种方案还有一个1。

那切掉1层，如果还有1，那说明在切掉之前是2，也就是说它在切掉之前是不同的（没有1）

没1：dp[i-j][j]和上面一样辣

复杂度

就是在左边选y个点，右边选k-y个点，使得左右两边点的质量的和相等

我们可以枚举一个和，枚举一个y，然后就完了

数位dp

先看个简单的

数位dp考虑方式：

我们用填数的方式来考虑，也就是考虑第i位填什么

我们最终填出来的数要保证有一个3，且最终的方案数就是答案

这里n就是上界

我们就枚举顶上界的那一位

f[i][0/1]表示i位之前随意填，且是否一定有3方案数（i是从高位向低位算，即最高位是第一位）

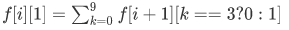
就是说，如果i的填三，则i的下一位就不用有三了

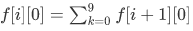
既然i和后面都没有3，那就只需要累加没有3的情况了

平衡树？平衡数！

我们设中心轴为mid

如果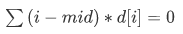，就说明这是个平衡数

但是我们现在不知道中心轴

f[i][k] 表示填到第i位（从高到低），上面式子的值为k的方案数

中心轴是可以任意取的？？？

那就是枚举中心轴，然后把所有算出来的平衡数的个数都加起来就是答案

如果一个非0数是平衡数，那么他的平衡轴只会有一个，所以不会算重

转移：f[i-1][k+(i-1-mid)*d[i-1]]+=f[i][k]

设有i个1的数有x个，那对答案的贡献就是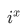

那对于每个i,只要求出来有多少个数有i个1即可

似乎是个数位dp

dp[i][j]到第i位，1的个数位j的数的数量

dp[i][j]=dp[i-1][j-1]+dp[i-1][j]

现场出的题：

区间[l,r]内，有多少个数的各个数位之和可以整除它本身

枚举数字和，看有多少个数%它为0，并且在填数过程中的数字和最终等于枚举的数字和

条件1：一维记上一个数，再来两个bool 记录上一个和上上个是否相同、是否有三个相同出现过

条件2：两个bool 记录是否有过8/4

dp[i][0/1][0/1][0/1][0/1][j]来搞

树形dp

一些前言

我们设f[u][0/1]表示u点是否选了的最大独立集

似乎真的很好理解叭

两遍dfs搞定

设f[i]是以i为lca的最远路径

求出i的每个儿子j的f[j],然后加上对应的边权，前两大的加起来就是f[i]

ans=f[root]

2:证明：

反证法：S是总集，如果去掉覆盖集之后不是独立集，那么说明后来的集合里面存在一条u向v的连边。但是连边应该在覆盖集里面

树链剖分？那个可以做n,m<=1e6

f[u]表示以u为根的子树中选取合法的树链的最大权值

1.u不在树链上f[u]=∑f[j]（j∈i'son）

2.u在树链上 :链的权值+不在链上的点的f值

总复杂度：O(n*m)

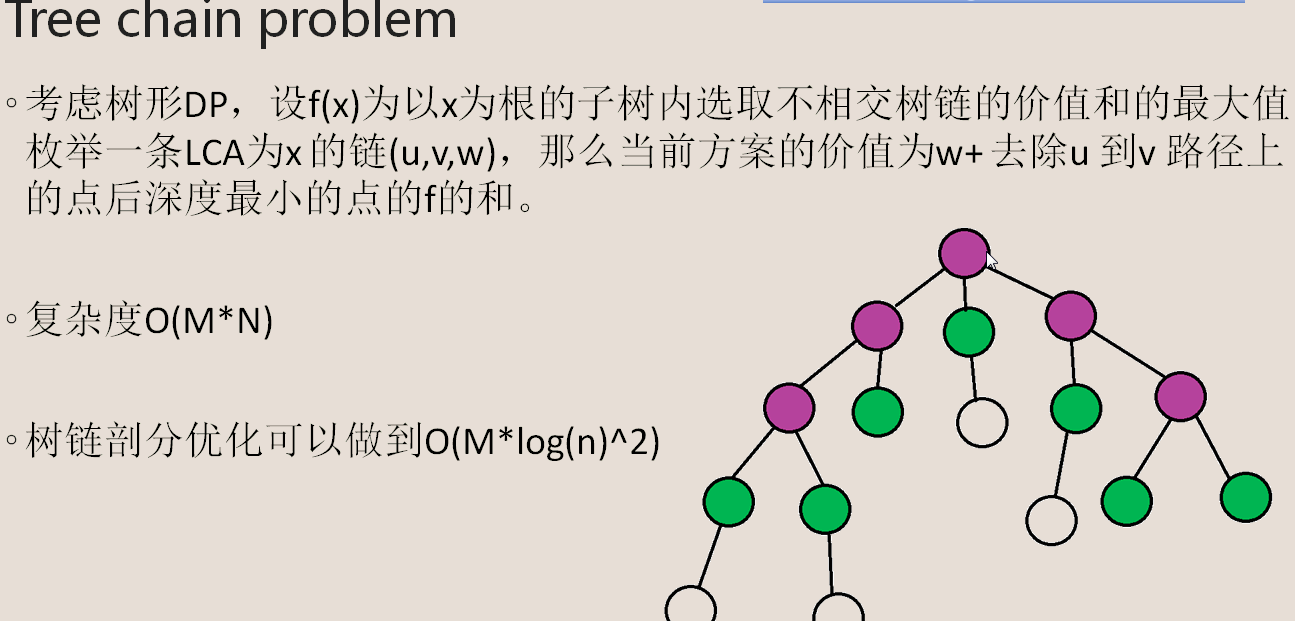
f[u][0/1][0/1]表示以u为根的子树，u亮不亮，u是否按下，把u的子树（不包含u）变成全部点亮状态的最小次数

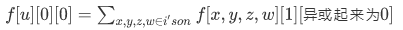
异或起来为0是指按了偶数次

好题之树上背包

不依赖：排序就好辣

有依赖：

dp[u][k]表示考虑u的子树的最大价值,选了k个物品

枚举每个孩子分配了多少个物品

背包增加：

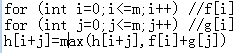
f[i]表示在f背包里面花i的钱的最大价值

g[i]，h[i]同理

变形h[i]=max(h[i],f[j]+g[i-j])

举个例子

//图

bzoj4033

f[u][j]表示u子树选择k个黑点的最大收益

u->fa[u]这条边对答案的贡献：j*(k-j)(黑点方面)

u子树里面有j个点，外面有k-j个点

白色点：(sz[u]-j)*(n-sz[u]-k+j)

同样也是里面的白点*外面的白点

emm直接看代码吧

所以到底是个什么鬼呢？

我们对dp数组进行复制，复制到g数组，然后拿g数组传到算孩子的dp值的函数里，最后考虑选这个子树和不选这个子树的情况

也就是说dp[i]=max(dp[i],g[son])

what's最大匹配？？？

选出来一些边，满足一个点最多在一个匹配中，最大的匹配

what'匹配？？？

就是一条边

what's点在匹配中？？？

就是点是选出来的边中的某一条边的端点

f[u][0/1]表示u是否和它的儿子进行匹配的最大值

因为线段树是一个二叉树，所以只有两个儿子

用L表示左儿子，R表示右儿子

f[u][1]=f[L][0]+f[R][0]

（如果它和两个儿子搞，那么两个儿子就不能和自己的儿子搞了）
如果它不和自己的儿子搞

①：两个儿子都和儿子的儿子搞

②：只有一个儿子和儿子的儿子搞

f[u][0]=max(f[L][0]+f[R][1],f[L][1]+f[R][0],f[L][1]+f[R][1]}

大概是这样叭

但是我们发现线段树的点数是nlogn的，在这个n的范围之下肯定是药丸的

所以我们要用上线段树一些优美的性质

我们注意到线段树会有很多长度相同的节点

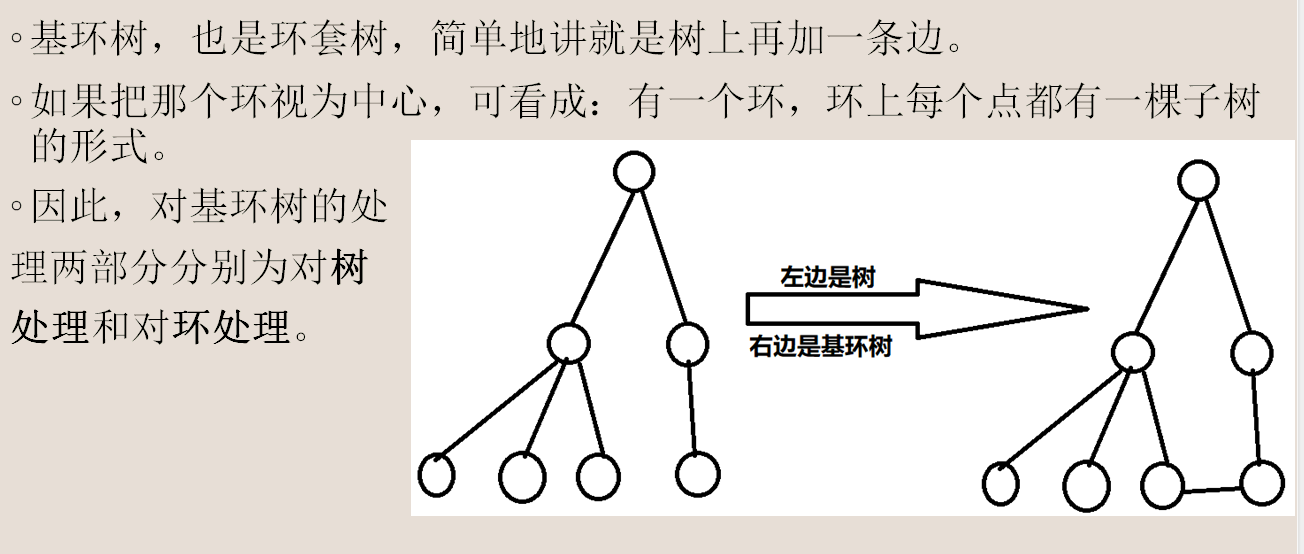
基环树：

在树上加一条边会构成一个环对吧

然后我们在树上随便加一条边就是基环树

我们枚举每条边的终点，如果到过，就发现了个环

基环内向树

求基环树最大独立集

当然这里是一个基环内向树（每个点只有一个出度）

性质：沿着出边一直走可以找到环

当然还有基环外向树（也就是入度为1）

把每条边反过来，就是一个基环内向树

直径有两种情况

①：过环：

max {di+dj+min(si-sj,sum-(si-sj))},其中si代表i到点1的距离，sum是总长

拆成个链：

假设我们拆成这个样子

si-sj<sum/2:di+dj+si-sj=max{dj-si}+di+si

si-sj>=sum/2:di+dj+sun-si+sj=max{dj+sj}+di-si

②：不过环：求树的直径