AdaGrad Algorithm and RMSProp
AdaGrad全称是Adaptive Gradient Algorithm,是标准Gradient Descent的又一个派生算法。标准Gradient Descent的更新公式为:
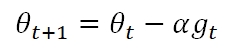
其中Learning Rate α对于Cost Function的各个feature都一样,但同一个α几乎不可能在各个feature上都表现完美,通常为了收敛,会选择较小的α。
而AdaGrad的主要思想是:在各个维度上使用不同的learning rate,从而加快函数收敛的速度。其公式为:
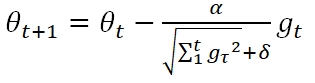
gt是t时刻目标函数的梯度,可以看到,依旧为各个feature设置了统一的α,但是通过历史梯度累计RMS作为分母来调节该learning rate。δ是一个很小的数例如10-7,仅仅为了分母不为0。
如果我们将等式右侧第二项看做一个整体。则标准Gradient Descent是,对t时刻梯度大的feature更新步子大,对t时刻梯度小的feature更新步子小。可以说Gradient Descent是衡量绝对大小的,但AdaGrad则不同,采取了“相对大与相对小”。使用当前时刻的梯度与历史梯度的RMS相比较,如果梯度变缓了,说明快要收敛了,那么步子调整的小一些;而如果梯度突然变大了,那证明参数需要大幅度更新了。
单AdaGrad算法虽然在凸函数(Convex Functions)上表现较好,但在非凸函数上却可能有局限。在深度学习训练中,Cost Function有可能会是很复杂的空间结构,有可能在某些平缓的结构上使用了很小的steps,但在某一时刻却有希望增大步伐。但上式的分母表示,优化的更新步伐和t时刻之前的所有时刻的梯度都相关,所以很有可能当算法希望增大步伐时,更新幅度已经衰减到很小,从而导致优化过程被困在某个局部最优点。
基于此,多大的Hinton教授提出了RMSProp,将AdaGrad和EMA结合起来。将上式分母的部分做成滑动的窗口,通过参数ρ来控制窗口的大小。从而,梯度的“相对大小”参照物,会丢弃遥远的历史,只与相邻窗口内的结构进行比较,来决定更新步幅的大小。梯度的EMA等于:
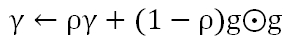
参数更新公式为:
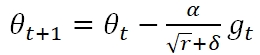
AdaGrad Algorithm and RMSProp的更多相关文章
- L21 Momentum RMSProp等优化方法
airfoil4755 下载 链接:https://pan.baidu.com/s/1YEtNjJ0_G9eeH6A6vHXhnA 提取码:dwjq 11.6 Momentum 在 Section 1 ...
- (转)分布式深度学习系统构建 简介 Distributed Deep Learning
HOME ABOUT CONTACT SUBSCRIBE VIA RSS DEEP LEARNING FOR ENTERPRISE Distributed Deep Learning, Part ...
- (转) An overview of gradient descent optimization algorithms
An overview of gradient descent optimization algorithms Table of contents: Gradient descent variants ...
- 第三十七节、人脸检测MTCNN和人脸识别Facenet(附源码)
在说到人脸检测我们首先会想到利用Harr特征提取和Adaboost分类器进行人脸检测(有兴趣的可以去一看这篇博客第九节.人脸检测之Haar分类器),其检测效果也是不错的,但是目前人脸检测的应用场景逐渐 ...
- An overview of gradient descent optimization algorithms
原文地址:An overview of gradient descent optimization algorithms An overview of gradient descent optimiz ...
- 基于MNIST数据的卷积神经网络CNN
基于tensorflow使用CNN识别MNIST 参数数量:第一个卷积层5x5x1x32=800个参数,第二个卷积层5x5x32x64=51200个参数,第三个全连接层7x7x64x1024=3211 ...
- Momentum
11.6 Momentum 在 Section 11.4 中,我们提到,目标函数有关自变量的梯度代表了目标函数在自变量当前位置下降最快的方向.因此,梯度下降也叫作最陡下降(steepest desce ...
- 第七章:网络优化与正则化(Part1)
任何数学技巧都不能弥补信息的缺失. --科尼利厄斯·兰佐斯(Cornelius Lanczos) 匈牙利数学家.物理学家 文章相关 1 第七章:网络优化与正则化(Part1) 2 第七章:网络优化与正 ...
- RNN 入门教程 Part 4 – 实现 RNN-LSTM 和 GRU 模型
转载 - Recurrent Neural Network Tutorial, Part 4 – Implementing a GRU/LSTM RNN with Python and Theano ...
随机推荐
- Linux mint启用内核转储
1.查看当前是否启动了内核转储: star@sky:~$ ulimit -c unlimited 2.如果上面显示为0,即没有开启,那么,直接执行 ulimit -c unlimited 就好了. 3 ...
- vue实现搜索功能
vue实现搜索功能 template 部分 <!-- 搜索页面 --> <template> <div> <div class="goback&qu ...
- Solr的学习使用之(五)添加索引数据
1.创建SolrServer类 SolrServer类:提供与Solr实例的连接与通信. 往Solr里添加索引数据,据说有好几种办法,这边利用SolrJ操作solr API完成index操作,具体So ...
- IC设计流程介绍
芯片设计分为前端设计和后端设计,前端设计(也称逻辑设计)和后端设计(也称物理设计)并没有统一严格的界限,涉及到与工艺有关的设计就是后端设计. 1. 规格制定 芯片规格,也就像功能列表一样 ...
- liunx-centos-基础命令详解(1) -主要内容来自 —https://www.cnblogs.com/caozy/p/9261224.html
关机:halt/poweroff :立刻关机reboot :立刻重启 shutdown -r now :立刻重启shutdown -h 00:00 :定时重启 now:立刻shutdown -h +n ...
- 线程工具类 - CyclicBarrier(循环栅栏)
CyclicBarrier官方文档 一.原理 CyclicBarrier是另外一种多线程并发控制实用工具.它和CountDownLatch非常类似,它也可以实现线程的计数等待,但它的功能比CountD ...
- 【串线篇】spring boot配置嵌入式servlet容器
SpringBoot默认使用Tomcat作为嵌入式的Servlet容器 问题? 一.如何定制和修改Servlet容器的相关配置 1.方法1修改和server有关的配置(ServerProperties ...
- 苹果IOS 12将使您的iPhone更安全,并有更强大的黑客保护
一年一度的IOS刷新正在进行中,苹果已经预览了它,beta测试者已经安装了它,当iPhone在9月份到货时我们其他人应该获得iOS12.虽然软件3-D表情符号和屏幕时间限制等功能在软件到货时可能会受到 ...
- Feign Dynamic URL
原创转载请注明出处:https://www.cnblogs.com/agilestyle/p/11811932.html Project Directory Maven Dependency < ...
- vuex的mapState方法来获取vuex的state对象中属性
有两种写法 1.首先在组件中引入vuex的mapState方法: 首先在组件中引入vuex的mapState方法: import { mapState } from 'vuex' 然后在compute ...
