hdu 4651 Partition(整数拆分+五边形数)

Partition

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 462    Accepted Submission(s): 262

Problem Description

How many ways can the numbers 1 to 15 be added together to make 15? The technical term for what you are asking is the "number of partition" which is often called P(n). A partition of n is a collection of positive integers (not necessarily distinct) whose sum equals n.
Now, I will give you a number n, and please tell me P(n) mod 1000000007.

 

Input

The first line contains a number T(1 ≤ T ≤ 100), which is the number of the case number. The next T lines, each line contains a number n(1 ≤ n ≤ 10⁵) you need to consider.

 

Output

For each n, output P(n) in a single line.

 

Sample Input

4
5
11
15
19

 

Sample Output

7
56
176
490

 

Source

2013 Multi-University Training Contest 5

 

Recommend

zhuyuanchen520

 

欧拉函数的倒数是分割函数的母函数，亦即：

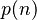的生成函数是

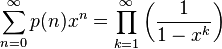   （1）

再

利用五边形数定理可得到以下的展开式：

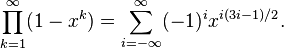 （2）

将（2）式带入（1）式，并乘到（1）式的左边，进行展开，合并同类项，根据非常数项的系数为0！！

 

即将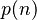生成函数配合五边形数定理，可以得到以下的递归关系式

 #include<stdio.h>
 typedef long long ll;
 const int mo=;
 ll p[];
 void pre()//打表，欧拉函数的倒数是分割函数的母函数！！！
 {
     p[]=;
     for(ll i=;i<=;i++)
     {
         ll t=,ans=,kk=;
         while()
         {
             ll tmp1,tmp2;
             tmp1=(*kk*kk-kk)/;
             tmp2=(*kk*kk+kk)/;
             if(tmp1>i)break;
             ans=(ans+t*p[i-tmp1]+mo)%mo;
             if(tmp2>i)break;
             ans=(ans+t*p[i-tmp2]+mo)%mo;
             t=-t;
             kk++;
         }
         p[i]=ans;
     }
 }
 int main()
 {
     pre();
     int T,n;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         printf("%lld\n",p[n]);
     }
 }