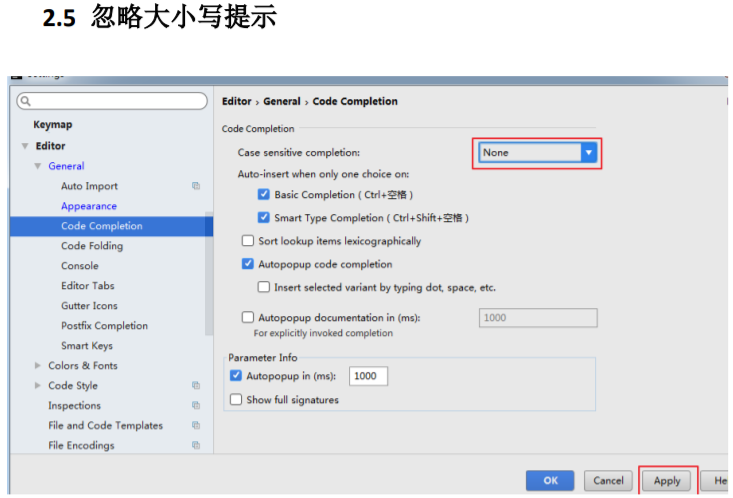
IntelliJ IDEA 2017.3尚硅谷-----忽略大小写提示的更多相关文章

  1. IntelliJ IDEA 2017.3尚硅谷-----鼠标悬浮提示

    建议不会的直接百度取消设置

  2. IntelliJ IDEA 2017.3尚硅谷-----插件的使用

    在 IntelliJ IDEA 的安装讲解中我们其实已经知道,IntelliJ IDEA 本身很多功能也都 是通过插件的方式来实现的.官网插件库:https://plugins.jetbrains.c ...

  3. IntelliJ IDEA 2017.3尚硅谷-----设置超过指定 import 个数，改为*

    (可忽略)

  4. IntelliJ IDEA 2017.3尚硅谷-----取消更新

  5. IntelliJ IDEA 2017.3尚硅谷-----缓存和索引的清理

  6. IntelliJ IDEA 2017.3尚硅谷-----生成 javadoc

    Locale:输入语言类型:zh_CN Other command line arguments:-encoding UTF-8 -charset UTF-8

  7. IntelliJ IDEA 2017.3尚硅谷-----配置 Maven

  8. IntelliJ IDEA 2017.3尚硅谷-----断点调试

  9. IntelliJ IDEA 2017.3尚硅谷-----版本控制(Version Control)

    不管是个人开发还是团队开发,版本控制都会被使用.而 IDEA 也很好的集成了 版本控制的相关结构. Git 的 msysGit 官网下载:https://git-scm.com/ Git 客户端 To ...

随机推荐

  1. JAVA StringUtils工具类

    org.apache.commons.lang Class StringUtils java.lang.Object org.apache.commons.lang.StringUtils publi ...

  2. 通过nginx实现多个域名访问同一个服务器

    一台服务器通过nginx配置多个域名(80端口)  参考:https://www.cnblogs.com/ruanjianlaowang/p/11182486.html 1. 问题描述 多个域名对应一 ...

  3. [tensorflow] tf.gather使用方法

    tf.gather:用一个一维的索引数组,将张量中对应索引的向量提取出来 import tensorflow as tf a = tf.Variable([[1,2,3,4,5], [6,7,8,9, ...

  4. Vuejs+elementUI项目，在进行打包时，要注意的问题

    注意:打包之前,需要注意修改一些地方 (1)若是前后端分离开发的,前端开发过程中可能会在api.js中设置访问路径为服务器所在电脑的ip:端口,打包前,最好将它改回localhost:8080 (2) ...

  5. H3C接口管理配置

    一.接口批量配置 当多个接口需要配置某功能(比如shutdown)时,需要逐个进入接口视图,在每个接口执行一遍命令,比较繁琐.此时,可以使用接口批量配置功能,对接口进行批量配置,节省配置工作量. 1. ...

  6. Java基础面试题总结二

    1,什么是字符串常量池? 字符串的分配,和其他的对象分配一样,耗费高昂的时间与空间代价.JVM为了提高性能和减少内存开销,在实例化字符串常量的时候进行了一些优化.为 了减少在JVM中创建的字符串的数量 ...

  7. python面试的100题（17）

    内存管理与垃圾回收机制 48.哪些操作会导致Python内存溢出,怎么处理? 内存溢出:你申请了10个字节的内存,但写入了大于10个字节的数据会导致内存溢出 内存溢出原因:1.内存中加载的数据量过于庞 ...

  8. 四、CentOS 7安装Oracle JDK

    CentOS 7安装Oracle JDK,查看Linux是否自带的JDK,如有openJDK,则卸载  CentOS7.1 JDK安装 1.卸载自带OPENJDK    用 java -version ...

  9. 一、c++语言基础

    1. 程序员的第一条代码"Hello,world!" #include <cstdio> //头文件,主要负责输入.输出 using namespace std;//C ...

  10. Python 编辑注意点

    文本编辑 Python: 绝对不能用Word和Windows自带的记事本. (1)Word保存的不是纯文本文件 (2)记事本会自作聪明地在文件开始的地方加上几个特殊字符(UTF-8 BOM),结果会导 ...