SIR模型预测新冠病毒肺炎发病数据

大家还好吗？
背景就不用多说了吧？本来我是初四上班的，现在延长到2月10日了。这是我工作以来时间最长的一个假期了。可惜哪也去不了。待在家里，没啥事，就用python模拟预测一下新冠病毒肺炎的数据吧。要声明的是本文纯属个人自娱自乐，不代表真实情况。
采用SIR模型，S代表易感者，I表示感染者，R表示恢复者。染病人群为传染源，通过一定几率把传染病传给易感人群，ta自己也有一定的几率被治愈并免疫，或死亡。易感人群一旦感染即成为新的传染源。
模型假设:
①不考虑人口出生、死亡、流动等情况，即人口数量保持常数。
②一个病人一旦与易感者接触就必然具有一定的传染力。假设 t 时刻单位时间内，一个病人能传染的易感者数目与此环境内易感者总数s(t)成正比，比例系数为β，从而在t时刻单位时间内被所有病人传染的人数为βs(t)i(t)。
③ t 时刻，单位时间内从染病者中移出的人数与病人数量成正比，比例系数为γ，单位时间内移出者的数量为γi(t)。
模型为

其中，β为感染系数，代表易感人群与传染源接触被感染的概率。γ为隔离(恢复)系数，我们对其倒数1/γ更感兴趣，代表了平均感染时间(average infectious period)。S(0)为初始易感人数，I(0)为初始感染人数。
按照[1]里面的代码模型的感染人数是这样的

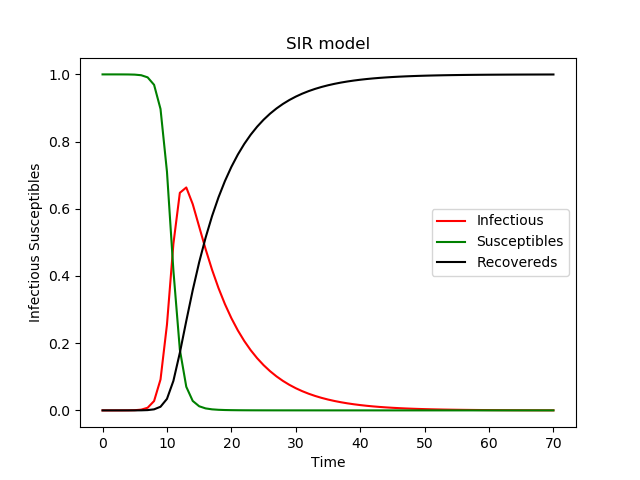
现在的问题就是利用现有的数据找到新冠肺炎的β值，γ值等数据了。先把数据拔下来吧。从[3]上扒数据，由于数据不多，就手工完成吧。保存到csv文件里。
然后把数据作图

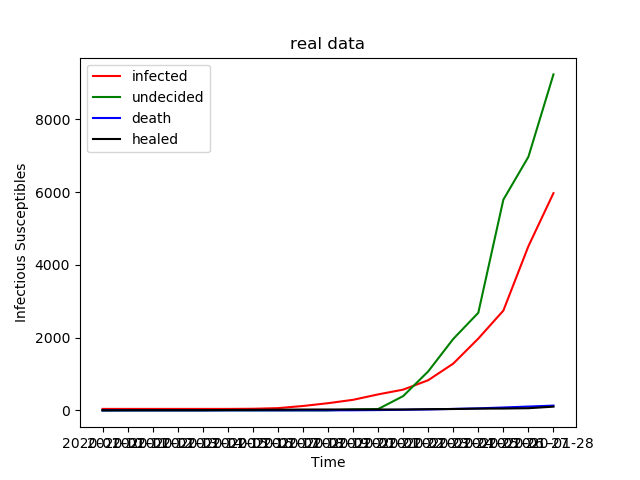
还有一个指标是再生数R0=β/γ，大于1时人群中大部分才被感染[4]。世卫组织1月23日的估计是R0在1.4到2.5之间[5]，最新的根据前425例发病数据的估计值为2.2[6]。
文章[7]中的按一般病毒性肺炎恢复期25天计算得到的γ值为0.04。
关于β值和初始易感人群，[7]的作者采用的方法是先估计一个区间，然后用最小二乘法找到最佳参数，β≈3.57*10^-5。S[0]的范围为5000-30000人。[7]文章里有matlab代码，我用python改写一下，由于对最小二乘法法的实现比较陌生，尝试了半天，最后我决定用最笨的办法——穷举法。就是用两个嵌套循环将范围内所有β值和S0值都试一遍，计算每次尝试结果与实际数据之间差值的平方和，平方和最小的一组β值和S0值用来做预测。代码如下:

γ值设定为0.04，即一般病程25天

用最小二乘法估计β值和初始易感人数

gamma = 0.04
S0 = [i for i in range(20000, 40000, 1000)]
beta = [f for f in np.arange(1e-7, 1e-4, 1e-7)]
# 定义偏差函数
def error(res):
    err = (data["感染者"] - res)**2
    errsum = sum(err)
    return errsum

# 穷举法，找出与实际数据差的平方和最小的S0和beta值
minSum = 1e10
minS0 = 0.0
minBeta = 0.0
bestRes = None

for S in S0:
    for b in beta:
        # 模型的差分方程
        def diff_eqs_2(INP, t):
            Y = np.zeros((3))
            V = INP
            Y[0] = -b * V[0] * V[1]
            Y[1] = b * V[0] * V[1] - gamma * V[1]
            Y[2] = gamma * V[1]
            return Y

        # 数值解模型方程
        INPUT = [S, I0, 0.0]
        RES = spi.odeint(diff_eqs_2, INPUT, t_range)
        errsum = error(RES[:21, 1])
        if errsum < minSum:
            minSum = errsum
            minS0 = S
            minBeta = b
            bestRes = RES
            print("S0=%d beta=%f minErr=%f" % (S, b, errsum))
print("S0 = %d β = %f" % (minS0, minBeta))

结果 S0 = 39000, β = 8e-6
上述程序耗时较长，只在探索时执行，完了就注释掉，用最优参数进行预测。

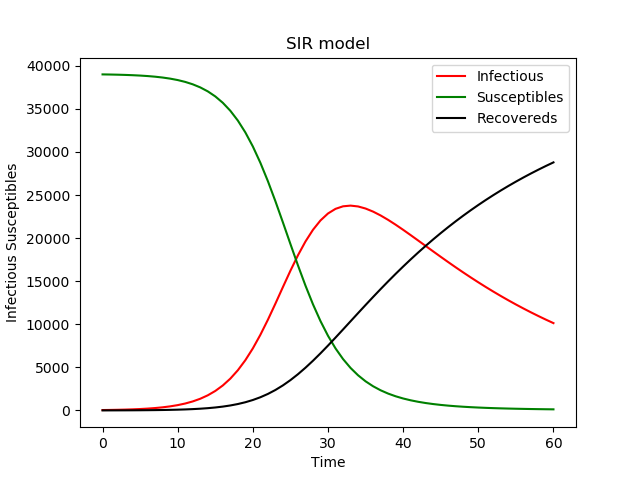
预测最大感染人数:23769 时间是在1月10日的33天后，也就是2月12日。
本文代码:https://github.com/zwdnet/2019-nCov-SIRmodel

再次声明:本文只是我个人在家无聊的游戏作品，不是正儿八经的预测。我也不是流行病学专业人士。祝疫情早日结束！武汉加油！中国加油！

参考文献:
[1]SIR模型实现, https://blog.csdn.net/huozi07/article/details/50450433
[2]百度百科SIR模型词条, https://baike.baidu.com/item/SIR%E6%A8%A1%E5%9E%8B
[3]疫情通报.http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml
[4]计算流行病学. https://www.csdn.net/article/1970-01-01/2816565
[5]关于新型冠状病毒（2019-nCoV）疫情的《国际卫 生条例（2005）》突发事件委员会会议的声明. https://www.who.int/zh/news-room/detail/23-01-2020-statement-on-the-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov)
[6]Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. https://www.nejm.org/doi/full/10.1056/NEJMoa2001316?query=featured_home
[7]基于SIR模型对新型冠状病毒疫情趋势的简单分析.https://zhuanlan.zhihu.com/p/104379096

我发文章的四个地方，欢迎大家在朋友圈等地方分享，欢迎点“在看”。
我的个人博客地址：https://zwdnet.github.io
我的知乎文章地址： https://www.zhihu.com/people/zhao-you-min/posts
我的博客园博客地址： https://www.cnblogs.com/zwdnet/
我的微信个人订阅号：赵瑜敏的口腔医学学习园地