第13届景驰-埃森哲杯广东工业大学ACM程序设计大赛----随手记录帖

这是跟学长学姐组队来打的最爽的一次比赛了，也可能是互相组队最后一次比赛了，南哥和楼学姐，省赛之后就退役了，祝他们能考研和面试都有happy ending！

虽然最后没有把F题的n^2约数的数学题写完，但体验了好久没有思考尽力的感觉，超级超级棒！！

A：跳台阶

签到题：直接输出1<<(n-1)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int main(){
    int t,n;
    cin>>t;
    while(t--){
        cin>>n;--n;
        printf("%d\n",<<n);
    }
}

D： psd面试

思路：最长回文子序列模板题啦，网搜一个随便都能找到的，f(i,j)代表从i到j的最长回文子序列。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=;
int n,dp[N][N];
char s[N];
int main(){
    while(~scanf("%s",s)){
        n=strlen(s);
        for(int i=;i<n;i++){
            if(s[i]>='A'&&s[i]<='Z'){
                s[i]=s[i]-'A'+'a';
            }
        }
        for(int i=n-;i>=;i--){
            dp[i][i]=;
            for(int j=i+;j<n;j++){
                dp[i][j]=dp[i+][j];
                if(s[i]==s[j]){
                    dp[i][j]=dp[i+][j-]+;
                }
                else {
                    dp[i][j]=max(dp[i+][j],dp[i][j-]);
                }
            }
        }
        printf("%d\n",n-dp[][n-]);
    }

}

 

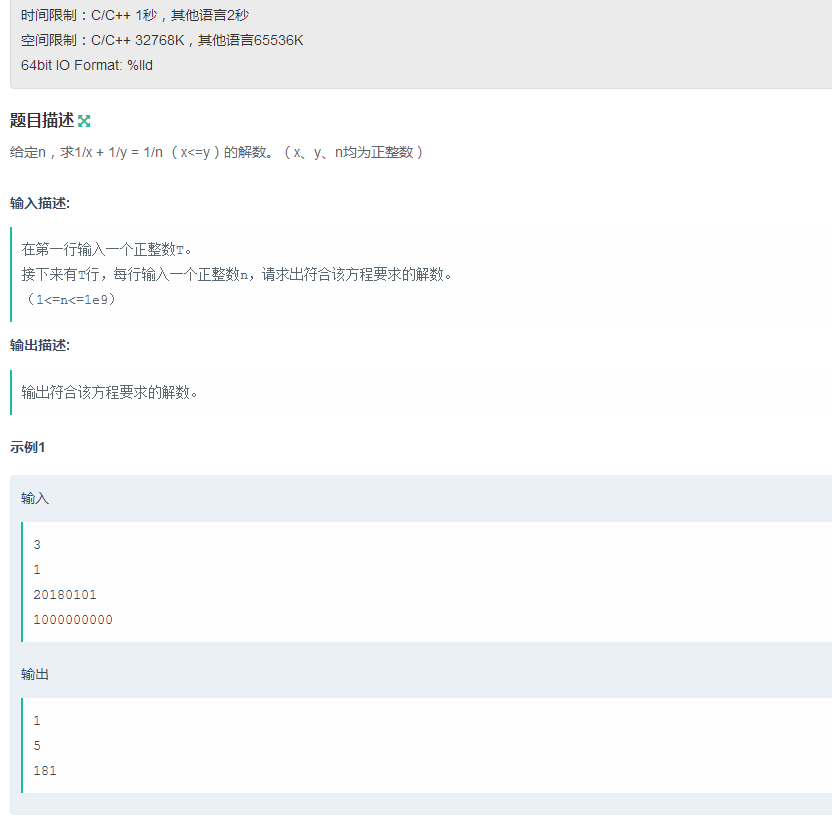
F：等式

思路：做以下解释：

　　首先考虑打表：由于x>=y,有1/x<=1/y,因此1/n-1/y<=1/y，即y<=2*n.这样，只需要在2*n范围之内枚举y，然后根据y尝试计算出x即可。这就是TOJ的4686题。但是！这里不行，因为n太大，每次循环如果数据都的是1e9，肯定会超时。

　　那么换种思路？

　　先看看暴力做的代码吧！

int sum = 0;
for(i=n+;i<=*n;i++)
{if((i*n)%(i-n)==)
      {
           sum++;
      }
}

注意看，是从n+1到n*2枚举(n*i)能否整除i-n；

那么做以下转化：

n*(n+k)/k  k属于[1,n]，求n*(n+k)/k是整数的k的个数。  发现式子可以化简为 n*n/k+1  。到这里，就好做了。 问题就转化为求n^2 中，在n之内的约数个数。

考虑到n^2是1e18次级，不太容易求。我们求n的约数即可。

做以下解释：12 = 2^2 * 3^1 约数个数为 指数+1的乘积。即(2+1)*(1+1) = 6

12^2 = 144 = 2^4 * 3 ^2  约数个数为 (4+1)*(2+1) = 15

　　　　　　可以看到，平方数的每一项都是原来的 (2倍指数值+1)

接下来就是欧拉函数+约数公式的问题了。最后注意一点。是如果最后剩下来的数如果是个大素数，那么别忘了乘以3。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        long long x,n,ans = ;
        cin>>n;
        x=n;
        for(long long i = ;i*i <= n;i++){
            if(n%i==){
                long long c = ;
                while(x%i == ){
                    c++;
                    x/=i;
                }
                ans *= (*c + );//需要乘以2倍的指数
            }
        }
        if(x != )ans *= ;//最后留下来是个大素数
        cout<<(ans+)/<<endl;
    }
    return ;
}

G：旋转矩阵

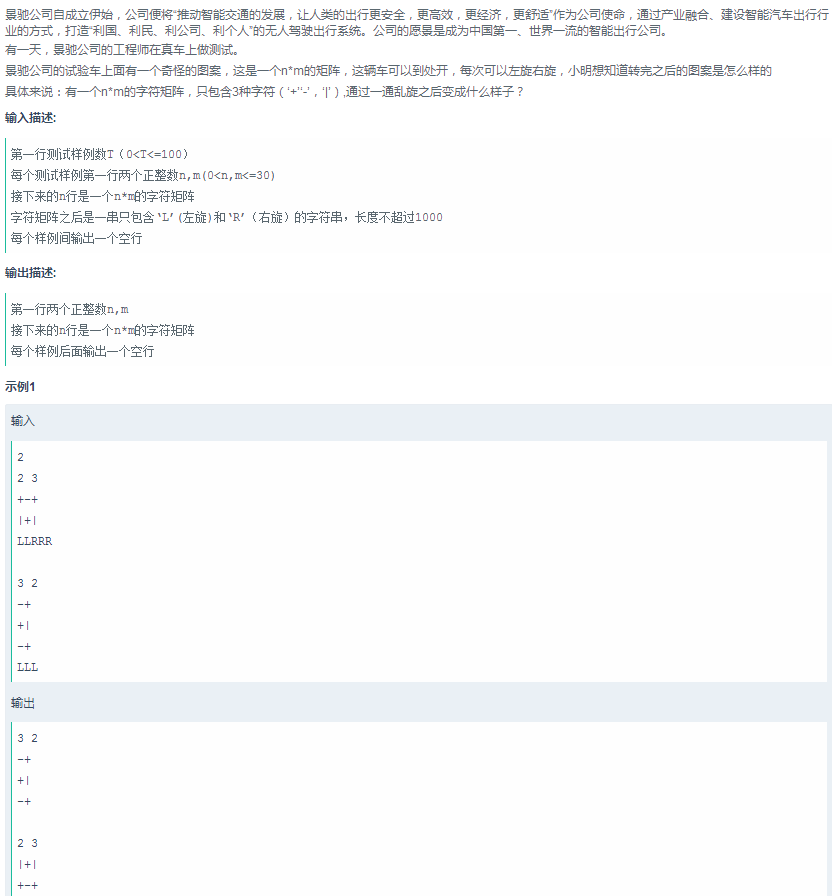
思路：大模拟！R可以转换为3个L，或者L可以转化为3个R，然后mod4，就算出了最后需要转几次，模拟做就行。（挺恶心的）

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

struct pic{
    char mp[][];
    int x,y;
}P[];

int main(){
    int flag=;
    int t;char s[];
    scanf("%d",&t);
    while(t--){
        int n,m;
        scanf("%d %d",&n,&m);
        P[].x=n;P[].y=m;
        for(int i=;i<n;i++){
            scanf("%s",P[].mp[i]);
        }
        scanf("%s",s);
        P[].y=n;P[].x=m;
        for(int i=;i<n;i++){
            for(int j=;j<m;j++){
                if(P[].mp[i][j]=='|')
                P[].mp[j][n-i-]='-';
                if(P[].mp[i][j]=='-')
                P[].mp[j][n-i-]='|';
                if(P[].mp[i][j]=='+')
                P[].mp[j][n-i-]='+';
            }
        }

        P[].x=n;P[].y=m;
        for(int i=;i<n;i++){
            for(int j=;j<m;j++){
                P[].mp[i][j]=P[].mp[n-i-][m--j];
            }
        }
        P[].x=m;P[].y=n;
        for(int i=;i<P[].x;i++){
            for(int j=;j<P[].y;j++){
                P[].mp[i][j]=P[].mp[m--i][n--j];
            }
        }

        int ans=,len=strlen(s);
        for(int i=;i<len;i++){
            if(s[i]=='L')ans+=;
            else ans+=;
            ans%=;
        }

        printf("%d %d\n",P[ans].x,P[ans].y);
        for(int i=;i<P[ans].x;i++){
            for(int j=;j<P[ans].y;j++){
                printf("%c",P[ans].mp[i][j]);
            }
            printf("\n");
        }
        printf("\n");
    }
}

I题：

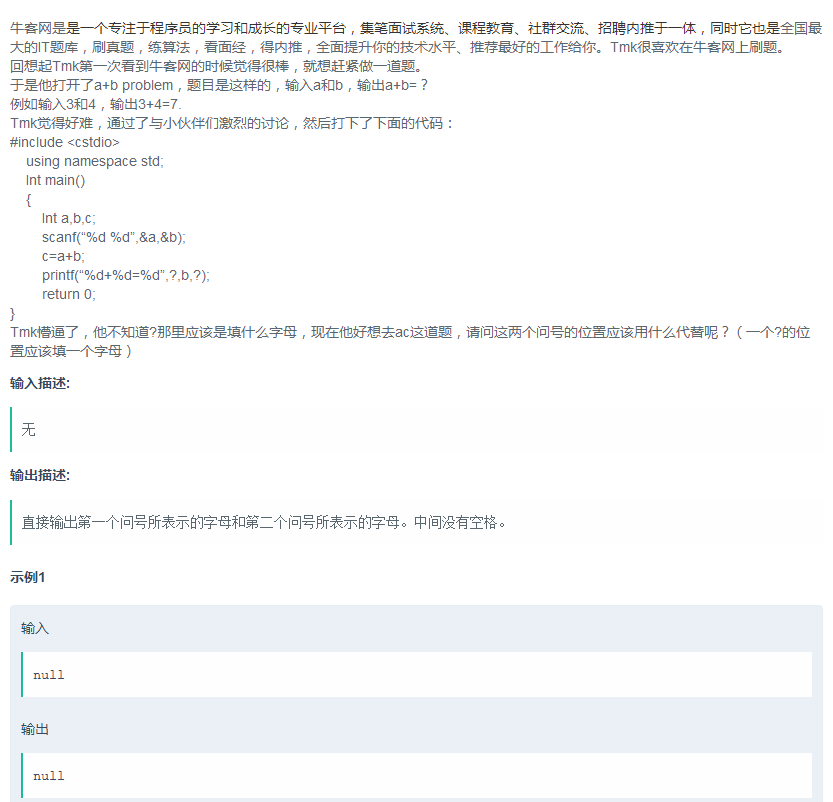
全场最水啦，直接输出字符串 ac 就行了，注意不要有空格。不附加代码了~

J：强迫症的序列

思路：找到最小的数Minnum，并且求个所有数的和sum。次数就是 sum 减去 n*Minnum；最后的数就是sum+次数*(n-1)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n,m,a[];
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%lld",&n);
        LL sum=,mi=;
        for(int i=;i<n;i++){
            scanf("%lld",&a[i]);
            mi=min(mi,a[i]);
            sum+=a[i];
        }
        LL c=sum-mi*n;
        LL x=sum+c*(n-);
        printf("%lld %lld\n",c,x/n);
    }
}

K题：密码

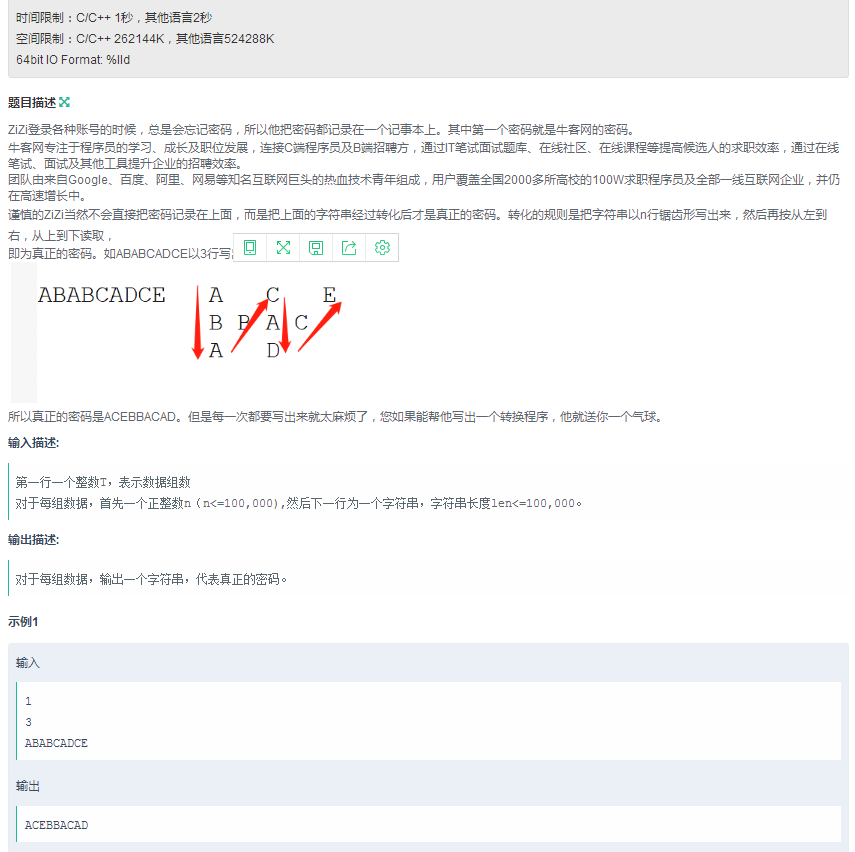
思路：前排吐槽千万别用数组存数什么的，直接输出！存下来再输出会超内存的说。

　　　大概就是找规律了，就是找这行的第一个跟下一个之间的规律，反正我找的就是：假设第一行第一个元素的位置是1，那么下一个就是1+(2*n-2)，再下一个就是1+2*(2*n-2)。。。最后是1+k*(2*n-2)。最后一行也是这样的

　　　中间的n-2行，规律是2*(n-i)和2*(i-1)交替着出现吧。具体可以看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
string s;
int main(){
    int n;
    int t;
    for(scanf("%d",&t);t--;){
        scanf("%d",&n);
        cin>>s;
        if(n == ){
            cout<<s<<endl;continue;
        }
        s.insert(,"&");
        int su = ;
        int ard = ,j = ;
        while(ard+j*(*n-) < s.size()){
            printf("%c",s[ard+j*(*n-)]);j++;
            su++;
        }
        for(int i =  ; i <= n -  ; i++){
            int k[] = {*(n-i),*(i-)};
            int sum = ,flag = ;
            while(i + sum < s.size()){
                printf("%c",s[i+sum]);
                if(!flag){
                    sum+=k[];
                    flag = ;
                }
                else{
                    sum+=k[];
                    flag = ;
                }
                su++;
            }
        }
        ard = n;j = ;
        while(ard+j*(*n-) < s.size()){
            printf("%c",s[ard+j*(*n-)]);j++;
            su++;
        }
        //printf("\n%d\n",su);
        puts("");
    }
}

L题：用来作弊的药水

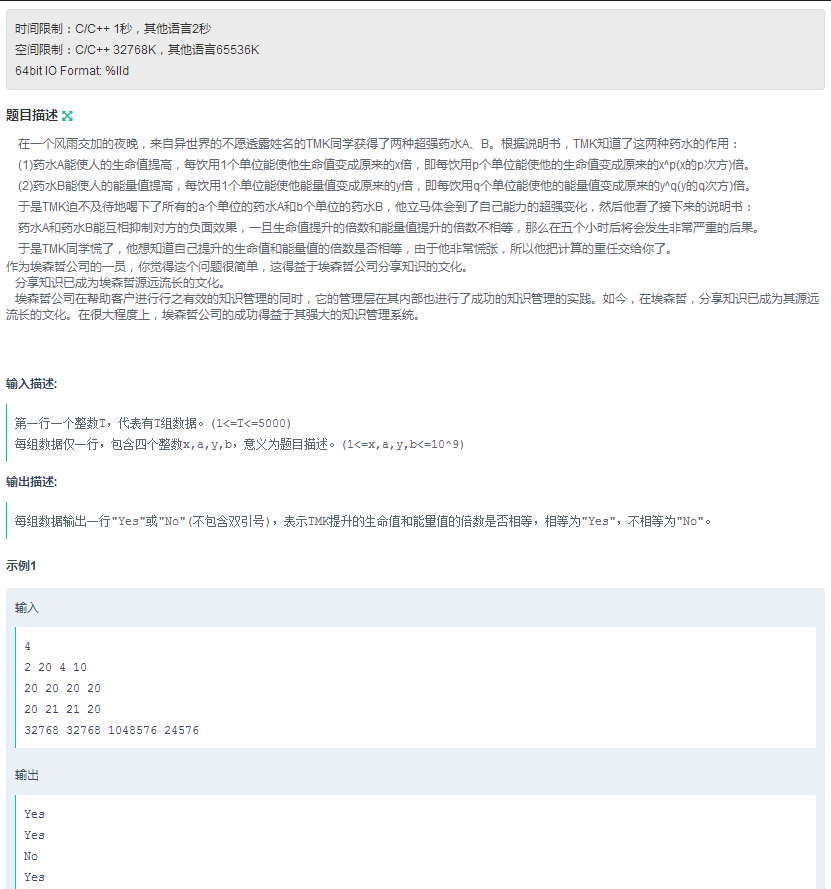
思路：好佩服学姐！思维转的超级快，题目就是让我们求x的a次 等不等于 y的b次。学姐秒看出，直接两边同时求个对数，然后变成了aln(x) 是不是等于 bln(y)。这样就非常非常好做了。

　　  随便写个long double判断一下就好了。代码附上！

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
long double x,y;
int n,a,b,c,d;
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d %d %d %d",&b,&a,&d,&c);
        x=a*log10(b);y=c*log10(d);
        if(fabs(x-y)<1e-){
            puts("Yes");
        }
        else puts("No");
    }
}