K-mer分析

0. 基本参数

　　基因组大小：G

　　Read读长：L

　　总Read条数：n_r

1. 碱基深度分布　　

　　单条Read测序覆盖到某一个碱基的概率：L/G

　　因为L/G很小，n_r很大，每个碱基覆盖深度服从泊松分布。

　　则每个碱基的覆盖深度的期望为：d_n=(L/G)*n_r

2. K-mer深度分布

　　假设基因组对K是unique的，可以得到G个不同的K-mer。

　　单条Read测序覆盖某个K-mer的概率：(L-K+1)/G

　　同样因为(L-K+1)/G很小，n_r很大，每个K-mer的覆盖深度服从泊松分布。

　　则每个K-mer的覆盖深度的期望为：d_k=((L-K+1)/G)*n_r

3. 通过K-mer分布估计基因组大小

　　可知总K-mer个数：n_k=(L-K+1)*n_r

　　通过统计K-mer分布可知K-mer深度期望：d_k=((L-K+1)/G)*n_r

　　则基因组大小：G=n_k/d_k

4. 碱基深度分布与K-mer深度分布的关系

　　d_n/d_k=L/(L-K+1)

5. K-mer深度分析工具

　　软件：KmerFreq_AR_v2.0

　　来源：SOAPdenovo2工具包，ftp://public.genomics.org.cn/BGI/SOAPdenovo2

　　命令： ./KmerFreq_AR_v2. -k -t -c - -p test test_read.lst >kmerfreq.cout >kmerfreq.cerr

 6. 常见K-mer分布

• 　正常

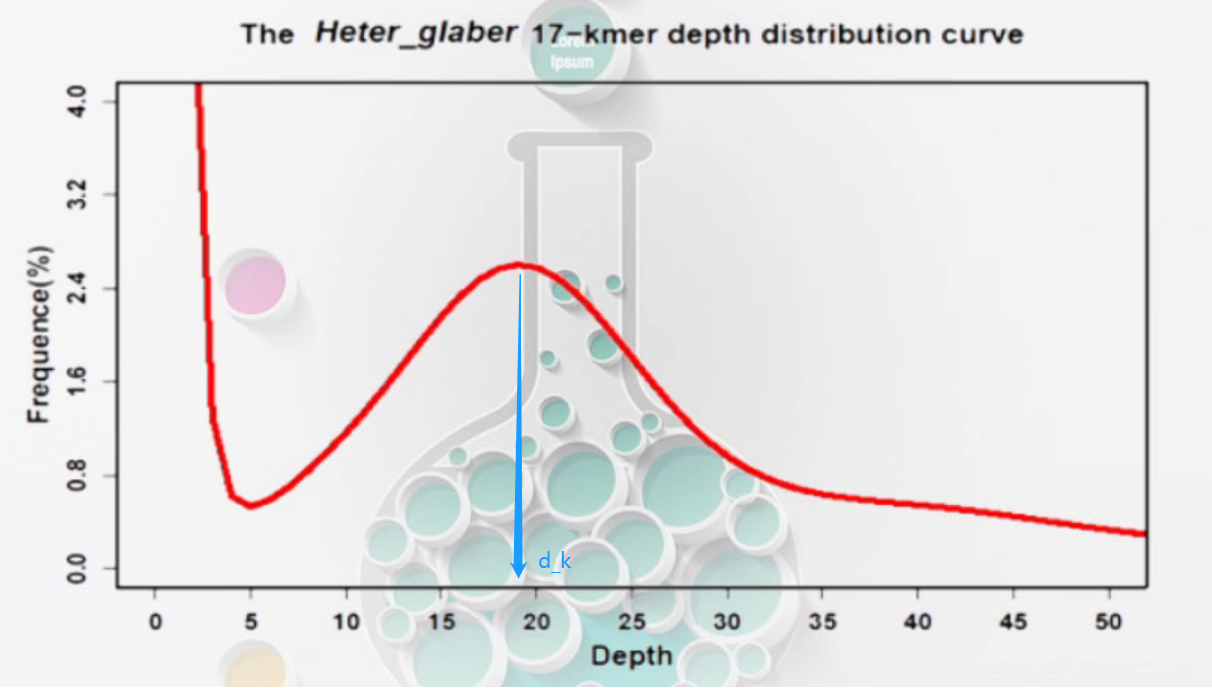
• 　高杂合

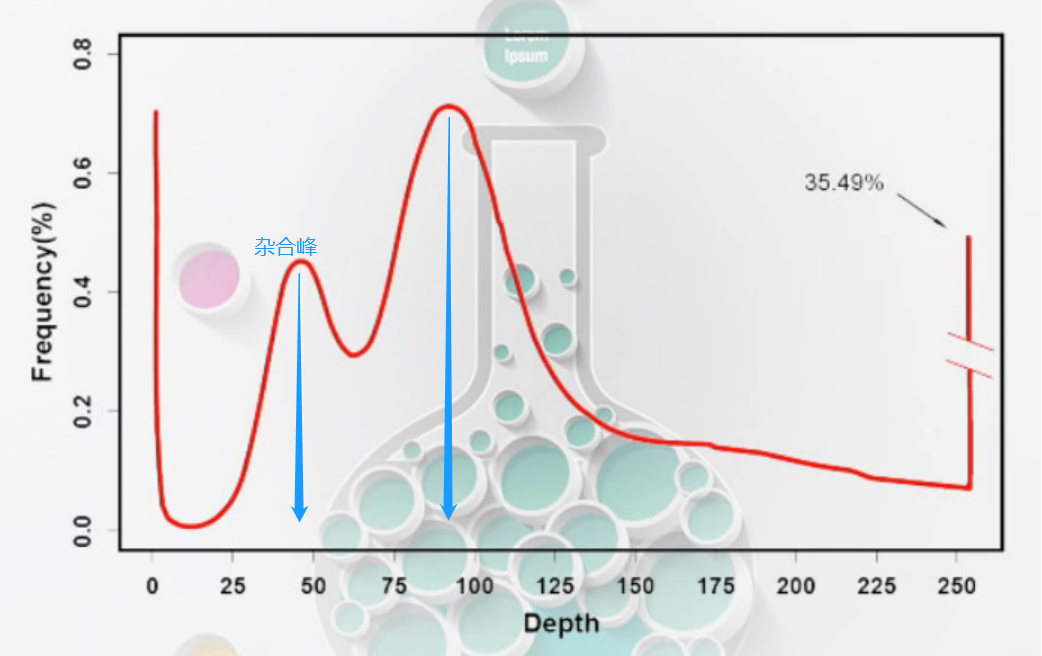
• 　高重复

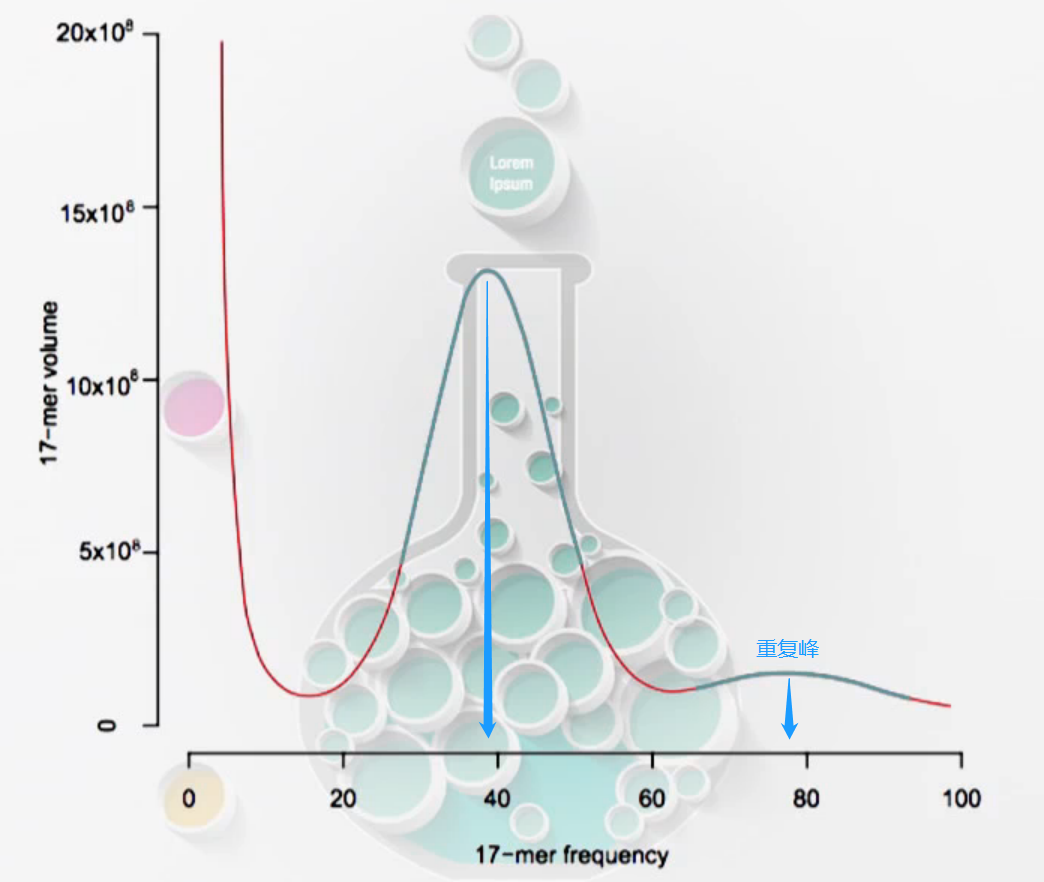
　　最左出现的为测序错误峰。