GBDT理解

一、提升树

提升方法实际采用加法模型(即基函数的线性组合)与前向分布算法。以决策树为基函数的提升方法称为提升树，boosting tree。对分类问题的决策树是二叉分类树，对回归问题的决策树是二叉回归树。提升树算法是AdaBoost算法的特殊情况。我的理解提升树分为普通提升树与梯度提升树，普通提升树每次拟合的是真实残差值，而梯度提升树拟合的是损失函数在当前模型的的负梯度。

普通提升树解决回归问题算法如下：

输入：训练数据集T={(x₁,y₁),(x₂,y₂),...,(x_n,y_n)}

输出：提升树f_M(x)

1) 初始化f₀(x)=0

2) 对m=1,2,...,M

　　a)计算残差 r_mi=y_i-f_m-1(x_i),i=1,2,..,n

　　b)拟合残差r_mi学习一个回归树，得到T(x;θ_m)

　　c)更新f_m(x)=f_m-1(x)+T(x;θ_m)

3) 得到回归问题提升树  f_M(x)=∑T(x;θ_m),  m=1,2,...,M

二、梯度提升树GBDT(Gradient Boosting Decision Tree)

普通提升树利用加法模型与前向分布算法实现学习的优化过程，这个时候损失函数可能是平方损失(如上例子)或者指数损失函数(AdaBoost就是指数损失函数，L=exp(-yf(x))),像平方损失函数，每棵树拟合的都是之前的残差值，这个能够直观去解释，但是如果是其它更一般的损失函数呢，如何去明确无误的一步步优化呢，有什么方法论去指引优化呢，优化的合理方向在哪呢？针对这一问题，Friedman于论文” Greedy Function Approximation…”中提出GBDT模型，为更一般形式的损失函数指明了优化方向。

其模型F定义为加法模型，x为输入样本，f为单棵树，w为每棵树的参数。

通过最小化损失函数求解最优模型：

也就是我们要找到一个使损失函数L最小的F，这里的损失函数跟构建单棵树所使用的损失函数不一样，是两码事，这里面的损失指的是所有树合并起来的整体损失。

与普通提升树不同的是，GBDT每次拟合的是损失函数L在当前模型F上的负梯度值，以此作为一个近似的残差值，拟合成一个新的回归树：

从上面几个公式我们就可以看到，梯度提升就是提升树的一种，也是前向分布算法实现的，所谓分布就是逐步提升，构建多棵树。

为什么GBDT每次拟合的是负梯度呢？

从我们的优化目标着手，我们的优化目标是让损失函数L越来越小，直到求解出一个最优的F，使得L到达最小值。那么我们可以把F整体做为一个变量去理解，跟我们之前的梯度下降法求解思路一样，让损失函数L对F进行求导，得到一个负梯度值，然后根据这个负梯度值作为新的值去拟合成一棵树，有n个样本，就会有n个负梯度值产生作为新的目标值y去拟合。F的初始值为F₀，每构造一棵树f，F=F_m-1+f，就相当于模型F在负梯度方向又向前走了一步，直到走到最优解。这就是GBDT的核心思路，跟我们平时利用梯度下降法求解最优参数θ思路其实一样。

GBDT具体算法流程如下：

其中的步长就是对应了xgboost中常说的shinkage技术，对应调参参数就是eta，是通过减少每棵树的学习输出值，削弱每棵树的影响，让后面的树有更大的学习空间，理论上是增加了树的个数，能够防止过拟合。比如：如果原始目标值是y=1，假如第一颗树就学到了0.9，那后面树学的信息就很少了，而且几棵树可能就让模型收敛了，这样模型整体的精确度很大程度上都依赖于第一颗树了，容易过拟合；如果将每棵树都乘以0.1，这样第一颗树输出就为0.09，后面还有很多信息可以学习，同时构造的树也多了，多方承担，有效了防止过拟合。

三、树模型的梯度提升算法与传统的梯度下降求参数区别

传统梯度下降法是在参数空间进行搜索，找到最优参数：

　　

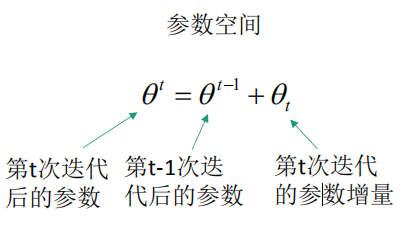
树模型的梯度提升算法，是在函数空间进行搜索，找到最优的函数，也是梯度下降，所谓的提升指的是模型整体精度提升：

四、树模型优缺点

优点：

　　可解释性强
　　可处理混合类型特征
　　具体伸缩不变性（不用归一化特征）
　　有特征组合的作用
　　可自然地处理缺失值
　　对异常点鲁棒
　　有特征选择作用

　　可扩展性强，容易并行

缺点：

　　缺乏平滑性（回归预测时输出值只能输出有限的若干种数值）
　　不适合处理高维稀疏数据