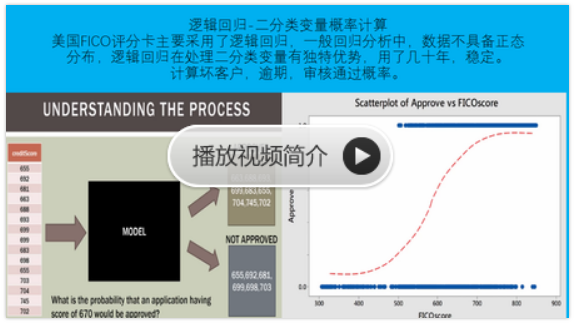
python+正态分布+蒙特卡洛预测男女身高概率！

sklearn实战-乳腺癌细胞数据挖掘

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

医药统计项目联系QQ：231469242

正态分布也称常态分布或常态分配，是连续随机变量概率分布的一种，是在数理统计的理论与实际应用中占有重要地位的一种理论分布。自然界人类社会，心理与教育中大量现象均按正态形式分布。例如能力的高低，学生成绩的好坏，人们的社会态度，行为表现以及身高、体重等身体状态。

（高斯Carl Friedrich Gauss）

正态分布是由阿伯拉罕·德莫弗尔(Abraham de Moivre)1733年发现的。其他几位学者如拉普拉斯(Marquis de Laplace)、高斯 (Carl Friedrich Gauss)对正态分布的研究也做出了贡献，故有时称正态分布为高斯分布。

正态分布的函数(又称密度函数)为

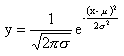
标准正态分布这两个参数分别为0与1。

标准正态分布的密度函数可写作：

（正态分布三个标准差的概率分布）

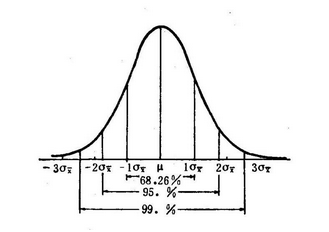
所有正太分布都可以转化成标准正态分布。

期望值μ决定了其位置，其标准差σ决定了分布的幅度。

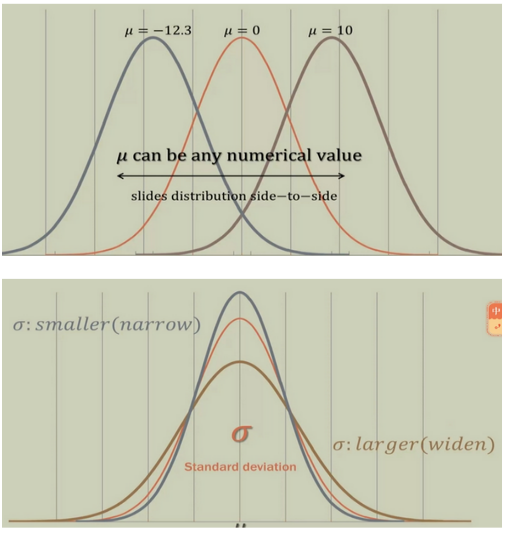
正态分布具有很大医学意义。正态分布的应用某些医学现象，如同质群体的身高、红细胞数、血红蛋白量、胆固醇等，以及实验中的随机误差，呈现为正态或近似正态分布。

我们提出一个常见的身高概率问题：假设男性平均身高175，标准差6；女性平均身高168, 标准差3；随机抽取一个女性和男性，女性高于男性随机概率是多少？

我们不需要通过复杂公式来计算。只需让计算机产生足够多的随机值来模拟计算，最后得到答案。

下面我们用Python的蒙特卡洛建模正态分布函数，解决这个男女身高概率问题。

（matplotlib绘制两个正态分布，红色表示女性，蓝色表示男性）

程序模拟10万个随机值，最后算出结果0.14727

即女性高于男性随机概率为0.14727

测试环境Anaconda Python2.7

源代码已经本人测试无问题

# -*- coding: utf-8 -*-

‘’’

By Toby ,Blog:

http://www.cnblogs.com/webRobot/

’’’
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import seaborn as sns
import math,pylab,matplotlib,numpy
from matplotlib.font_manager import FontProperties
#设置中文字体
font=FontProperties(fname=r"c:\windows\fonts\simsun.ttc",size=15)
#测试n次
n=100000
#标准正太分布
normalDistribution=stats.norm(175,6)
#方差较大正态分布
normalDistribution1=stats.norm(168,3)
#一次随机
def Random_single():
    array_male=normalDistribution.rvs(1)
    array_female=normalDistribution1.rvs(1)
    male=array_male[0]
    female=array_female[0]
    if female>male:
       return True
    else:
       return False
#n次随机，返回count（女性高于男性的次数）
def Multiple_random(n):
    count=0
    for i in range(n):
       value=Random_single()
       if value==True:
          count+=1
    return count
# 计算女性高于男性概率
def Probability(n):
    count=Multiple_random(n)
    p=count*1.0/n
    return p
probability=Probability(n)
print '随机次数',n
print '女性高于男性概率:',probability
#绘图
x=np.arange(60,220)
y=normalDistribution.pdf(x)
y1=normalDistribution1.pdf(x)
plt.plot(x,y,label="male")
plt.plot(x,y1,'r',label="female")
plt.xlabel("x")
plt.ylabel("probability density")
#plt.title("Normal distribution:mean=%.1f,standard
deviation=%.1f"%(mean,std))
plt.title("Normal distribution")
plt.legend()
plt.show()

python风控评分卡建模和风控常识

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share