使用Python和SymPy推导斯特林公式

引言

斯特林公式(Stirling’s Approximation)是一种用来近似计算阶乘的数学公式。它是数学分析中非常重要的近似公式之一，尤其在概率论、统计学、物理学等领域中广泛应用。本文将使用 Python 中的数学符号计算库 SymPy 推导斯特林公式，帮助大家更好地理解它的推导过程。

1.阶乘的定义

阶乘是一个常见的数学概念，表示一个正整数的连乘积。通常用感叹号表示，如下所示：

\[n! = n \times (n-1) \times (n-2) \times \dots \times 1
\]

例如，5! 就是 \(5 \times 4 \times 3 \times 2 \times 1 = 120\)

然而，当 n 很大时，计算阶乘变得非常困难。因此，我们需要一个近似方法来简化计算，这就是斯特林公式的作用所在。

2.斯特林公式

斯特林公式给出了 n! 的一个近似表达式。公式如下：$$n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n$$

其中：

• n 是阶乘的数值。
• e 是自然对数的底数(大约等于 2.71828)。
• \(\pi\) 是圆周率。

使用 SymPy 推导斯特林公式

SymPy 是一个强大的 Python 库，可以进行符号计算(即精确计算)，它可以帮助我们推导数学公式。我们通过它来推导斯特林公式，并理解每一步的过程。

# coding=utf-8
import sympy as sp
import numpy as np
import matplotlib

matplotlib.use('Agg')
import matplotlib.pyplot as plt
import math

# 定义变量
n = sp.symbols('n')

# 定义阶乘的符号表示
factorial_n = sp.factorial(n)

# 定义斯特林公式的近似表达式
stirling_approximation = sp.sqrt(2 * sp.pi * n) * (n / sp.exp(1)) ** n

# 打印斯特林公式的推导
print(stirling_approximation)

# 比较阶乘和打印斯特林公式
error = sp.limit(factorial_n / stirling_approximation, n, sp.oo)
print(error)

n_values = np.arange(1, 50)
factorial_values = [math.factorial(n) for n in n_values]  # 使用 math.factorial 计算阶乘
stirling_values = [np.sqrt(2 * np.pi * n) * (n / np.exp(1)) ** n for n in n_values]

errors = np.abs(np.array(factorial_values) - np.array(stirling_values))

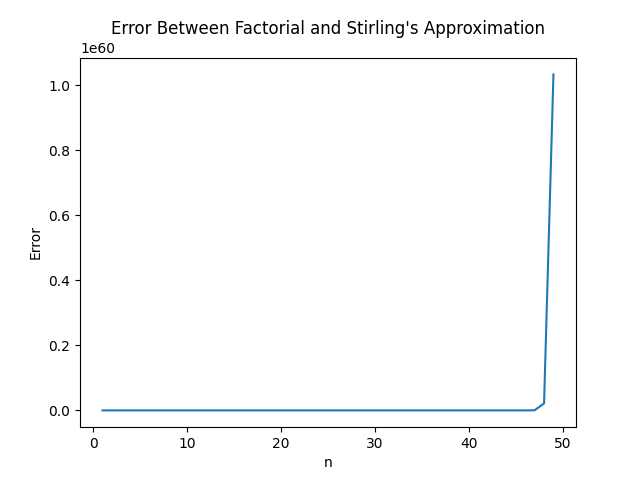
# 绘图
plt.plot(n_values, errors)
plt.xlabel('n')
plt.ylabel('Error')
plt.title('Error Between Factorial and Stirling\'s Approximation')
plt.savefig('stirling_error_plot.png')

输出结果

sqrt(2)*sqrt(pi)*sqrt(n)*(n*exp(-1))**n
1

总结

斯特林公式为我们提供了一个有效的计算阶乘的近似方法，尤其在 n 很大的情况下，计算阶乘变得更加高效。通过 Python 和 SymPy，我们能够轻松推导和验证斯特林公式，并能够通过图形展示其精度。

希望这篇文章能够帮助你更好地理解斯特林公式的推导过程及其应用。如果你对数学公式的推导或 Python 编程感兴趣，可以继续深入学习更多内容！