主观经验 和 客观事实:后验概率

Subjective主观经验: 先验概率 & 似然概率

Objective客观事实: 后验概率 & 条件概率

Floyd(弗落伊得)最短路线算法

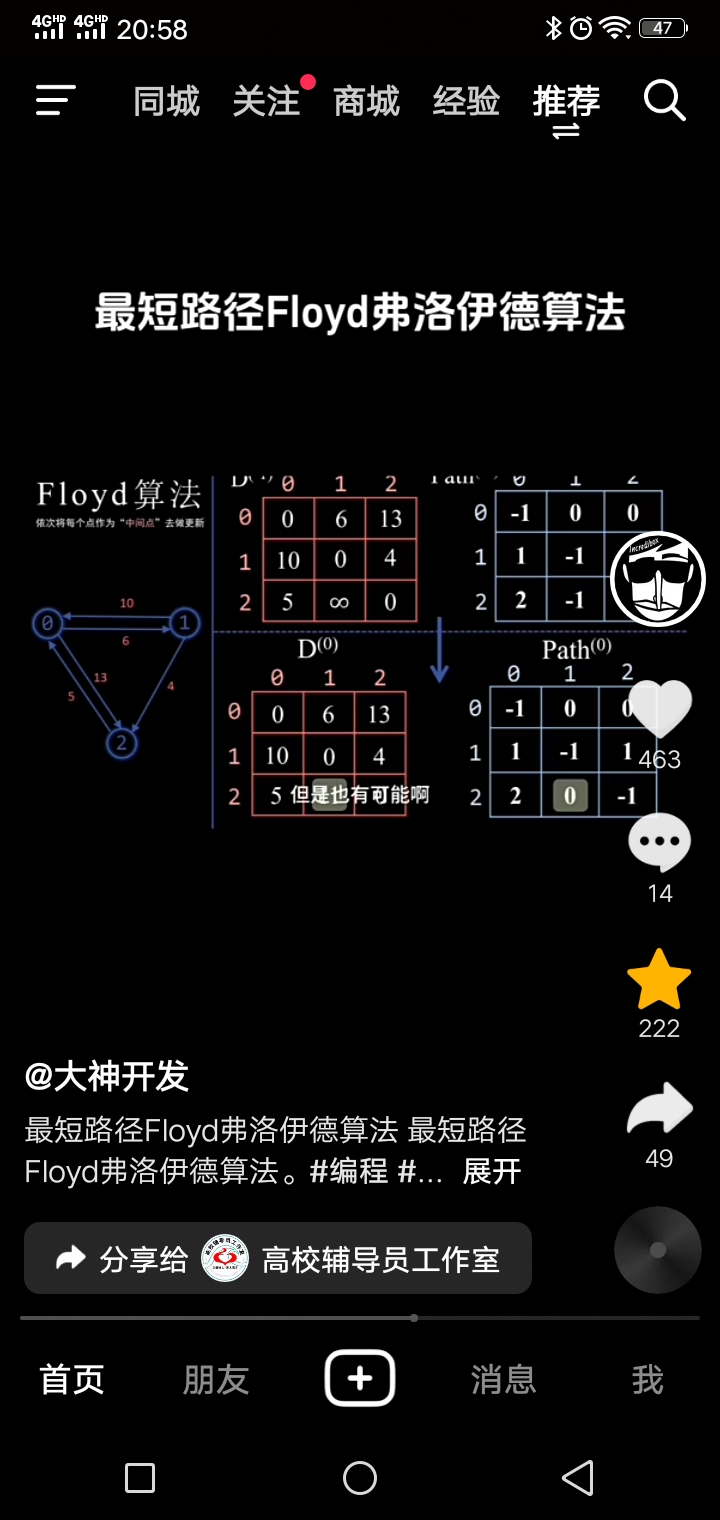
SciTech-BigDataAIML-Algorithm: 主观经验:先验概率&似然概率 和 客观事实:后验概率&条件概率 + Floyd(弗落伊得)最短路线算法的更多相关文章

  1. EM 最大似然概率估计

    转载请注明出处 Leavingseason http://www.cnblogs.com/sylvanas2012/p/5053798.html EM框架是一种求解最大似然概率估计的方法.往往用在存在 ...

  2. 最大似然概率（MLE）和最大后验概率（MAP）

    https://blog.csdn.net/u011508640/article/details/72815981

  3. 【转】Algorithms -离散概率值（discrete）和重置、洗牌（shuffle）算法及代码

    离散概率值(discrete) 和 重置\洗牌(shuffle) 算法 及 代码 本文地址: http://blog.csdn.net/caroline_wendy/article/details/1 ...

  4. 机器学习基础系列--先验概率 后验概率 似然函数 最大似然估计(MLE) 最大后验概率(MAE) 以及贝叶斯公式的理解

    目录 机器学习基础 1. 概率和统计 2. 先验概率(由历史求因) 3. 后验概率(知果求因) 4. 似然函数(由因求果) 5. 有趣的野史--贝叶斯和似然之争-最大似然概率(MLE)-最大后验概率( ...

  5. 朴素贝叶斯分类器及Python实现

    贝叶斯定理 贝叶斯定理是通过对观测值概率分布的主观判断(即先验概率)进行修正的定理,在概率论中具有重要地位. 先验概率分布(边缘概率)是指基于主观判断而非样本分布的概率分布,后验概率(条件概率)是根据 ...

  6. EM算法浅析(一)-问题引出

    EM算法浅析,我准备写一个系列的文章: EM算法浅析(一)-问题引出 EM算法浅析(二)-算法初探 一.基本认识 EM(Expectation Maximization Algorithm)算法即期望 ...

  7. MLLib实践Naive Bayes

    引言 本文基于Spark (1.5.0) ml库提供的pipeline完整地实践一次文本分类.pipeline将串联单词分割(tokenize).单词频数统计(TF),特征向量计算(TF-IDF),朴 ...

  8. 主题模型（概率潜语义分析PLSA、隐含狄利克雷分布LDA）

    一.pLSA模型 1.朴素贝叶斯的分析 (1)可以胜任许多文本分类问题.(2)无法解决语料中一词多义和多词一义的问题--它更像是词法分析,而非语义分析.(3)如果使用词向量作为文档的特征,一词多义和多 ...

  9. HMM隐马尔科夫算法(Hidden Markov Algorithm)初探

    1. HMM背景 0x1:概率模型 - 用概率分布的方式抽象事物的规律 机器学习最重要的任务,是根据一些已观察到的证据(例如训练样本)来对感兴趣的未知变量(例如类别标记)进行估计和推测. 概率模型(p ...

  10. EM算法(Expectation Maximization Algorithm)初探

    1. 通过一个简单的例子直观上理解EM的核心思想 0x1: 问题背景 假设现在有两枚硬币Coin_a和Coin_b,随机抛掷后正面朝上/反面朝上的概率分别是 Coin_a:P1:-P1 Coin_b: ...

随机推荐

  1. ctf.show刷题记录_web(1-10)

    ctf平台(ctfshow) `https://ctf.show/ 1.签到 解题:base64解码 ctfshow{0da357d0-359b-47e1-80dc-5c02212725e5} 2.w ...

  2. linux 指定运行级别

    目录 基本介绍 指定运行级别 基本介绍 0:关机 1:单用户 2:多用户状态没有网络服务 3:多用户状态有网络服务 4:系统未使用保留给用户 5:图形界面 6:系统重启 常用的运行级别是3和5,也可以 ...

  3. Mybatis 框架课程第四天

    目录 1 Mybatis 延迟加载策略 1.1 何为延迟加载 1.2 实现需求 1.3 使用 assocation 实现延迟加载 1.3.1 账户的持久层 DAO 接口 1.3.2 账户的持久层映射文 ...

  4. 【ROS】6.1 中间人攻击移动过程

    原视频 中间人攻击 实验目的 ARP欺骗可以作为中间人攻击的一个起手式.前一个实验我们完成了ARP欺骗,在本章实验中,我们将会在上一个实验的基础上,针对键盘控制过程的报文进行修改,使键盘控制异常. 本 ...

  5. 私有资产测绘&安全流水线Shovel

    私有资产测绘&安全流水线Shovel(Preview)发布 发布版本:Shovel-v0.1.7 当前项目发布版本 Shovel-v0.1.7(预览版) | 企业级资产测绘管理,开启资配漏补新 ...

  6. vue3微前端架构——基于蚂蚁qiankun框架

    楔子 首先,目前qiankun框架尚不支持vite, 微应用不能使用vite创建, 即使只是生产环境加的载微应用也不行, 因为vite打包代码时,内部的esbuild会tree shake掉与qian ...

  7. Disruptor—2.并发编程相关简介

    大纲 1.并发类容器 2.volatile关键字与内存分析 3.Atomic系列类与UnSafe类 4.JUC常用工具类 5.AQS各种锁与架构核心 6.线程池的最佳使用指南 1.并发类容器 (1)C ...

  8. Mac 终端下svn常用命令的使用

    svn基本的操作流程 刚刚进入一个新的公司,让我接手一个正在进行的项目,我打开终端写下了:svn co svn://192.168.1.1/pro/domain 然后就可以在当前目录里面找到一个叫do ...

  9. 校内NOI模拟测试007T1 送分(score) “简单”的计数

    问题描述 校内评测链接 良心出题人准备为大家送出大量的分数. 出题人生成了一个序列,其中第\(\)个元素为\(a_i\). 定义一个集合\(\)的分值为 \[F(S,x) = \sum_{T \sub ...

  10. 关于cc3复现以及绕过思路

    关于cc3复现以及绕过思路 (文章简略许多,可以的话,可以看看之前之前发布的文章) 绕过思路:动态加载字节码绕过Runtime,exec被过滤 在前面两个篇章中我们学习了cc1,cc6和动态加载字节码 ...