【转】持续集成 Sonar 平台搭建及 Sonar 自定义规则打包部署篇

引言

基于阿里开发手册的sonar自定义插件工程 开源地址: https://github.com/tigerge000/sonar-java-custom-rules.git
由于最近来问童鞋，就算写出了Demo，但部署到sonar平台后，运行还是出现各种问题，因此我这边把 sonar平台部署，插件打包，插件导入等一些列重新补一篇
sonar自定义插件开发文章: https://testerhome.com/topics/8105

Linux下安装Sonar

下载地址: https://www.sonarqube.org/downloads/
安装环境说明:
服务器:192.168.3.14
已安装mysql+java+maven+git
项目存储路径: /home/admin/testrelease/

sonar环境配置

(一) 修改mysql配置文件

default-storage-engine=INNODB
innodb_buffer_pool_size=256M
innodb_log_file_size=256M
max_allowed_packet=100M
datadir=/var/lib/mysql
socket=/var/lib/mysql/mysql.sock
user=mysql
# Disabling symbolic-links is recommended to prevent assorted security risks
symbolic-links=0
[mysqld_safe]
log-error=/var/log/mysqld.log
pid-file=/var/run/mysqld/mysqld.pid

重启mysql
service mysql restart

(二)新建sonar数据库

 

安装sonarqube

unzip sonarqube-6.2.zip
cp -r sonarqube-6.2 /usr/local

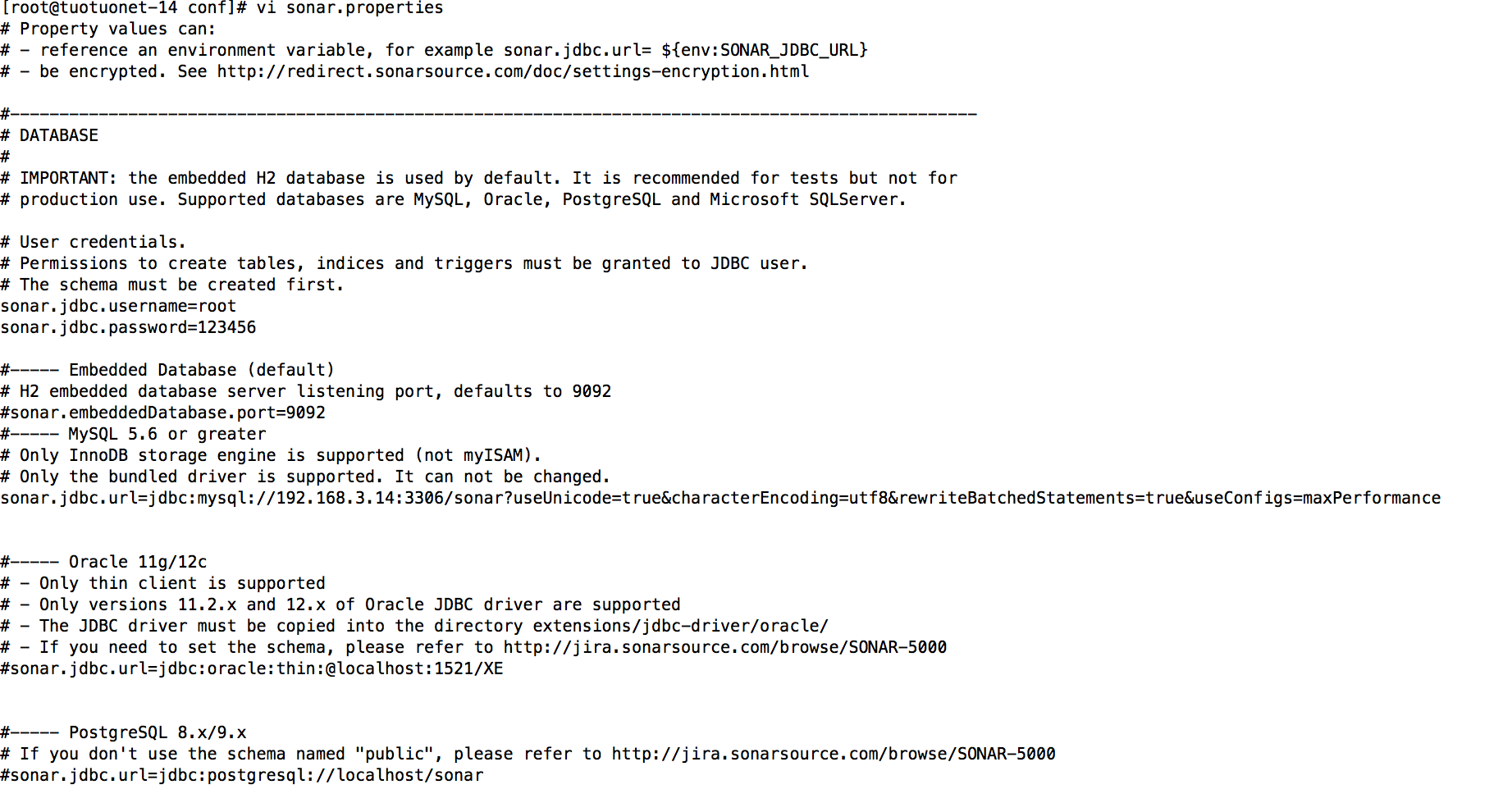
(一)修改sonarqube配置文件

 

(二)启动服务

路径:/usr/local/sonarqube-6.2/bin/linux-x86-64
[root@tuotuonet-14 linux-x86-64]# ./sonar.sh start

 

sonar-runner配置

插件地址:https://docs.sonarqube.org/display/SCAN/Analyzing+with+SonarQube+Scanner
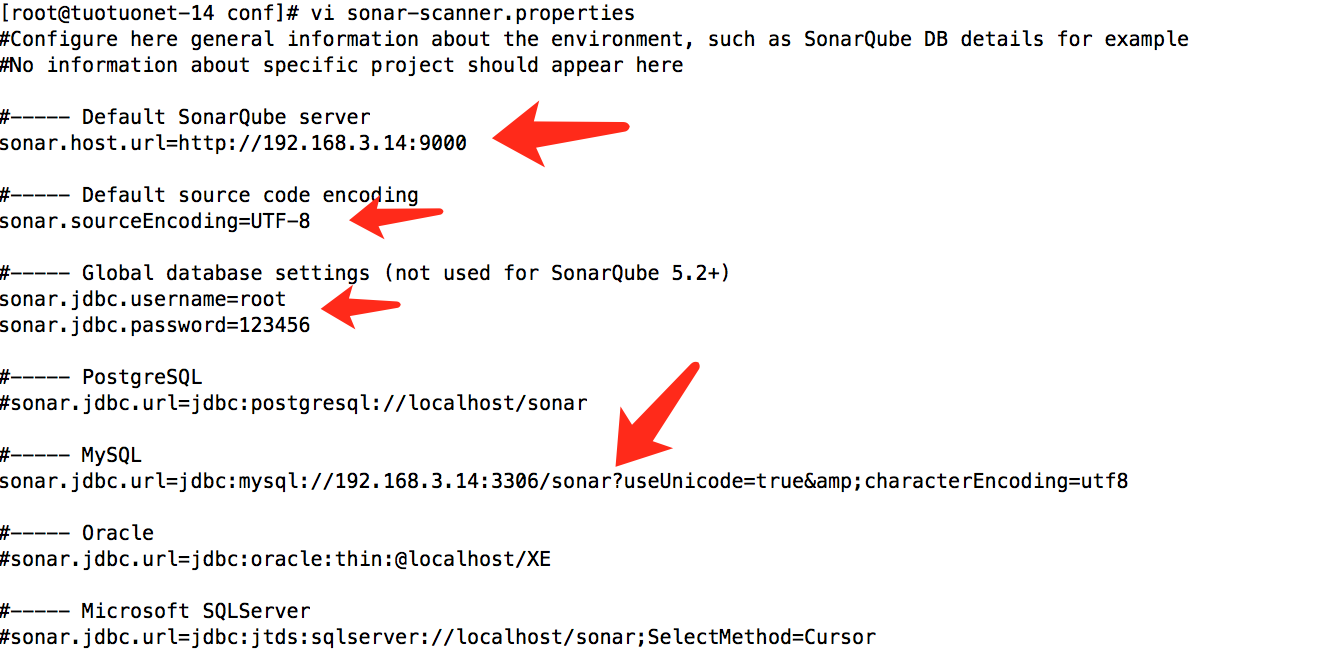
(1)修改配置文件sonar-scanner.properties
/usr/local/sonar-scanner-2.8/conf/sonar-scanner.properties

 

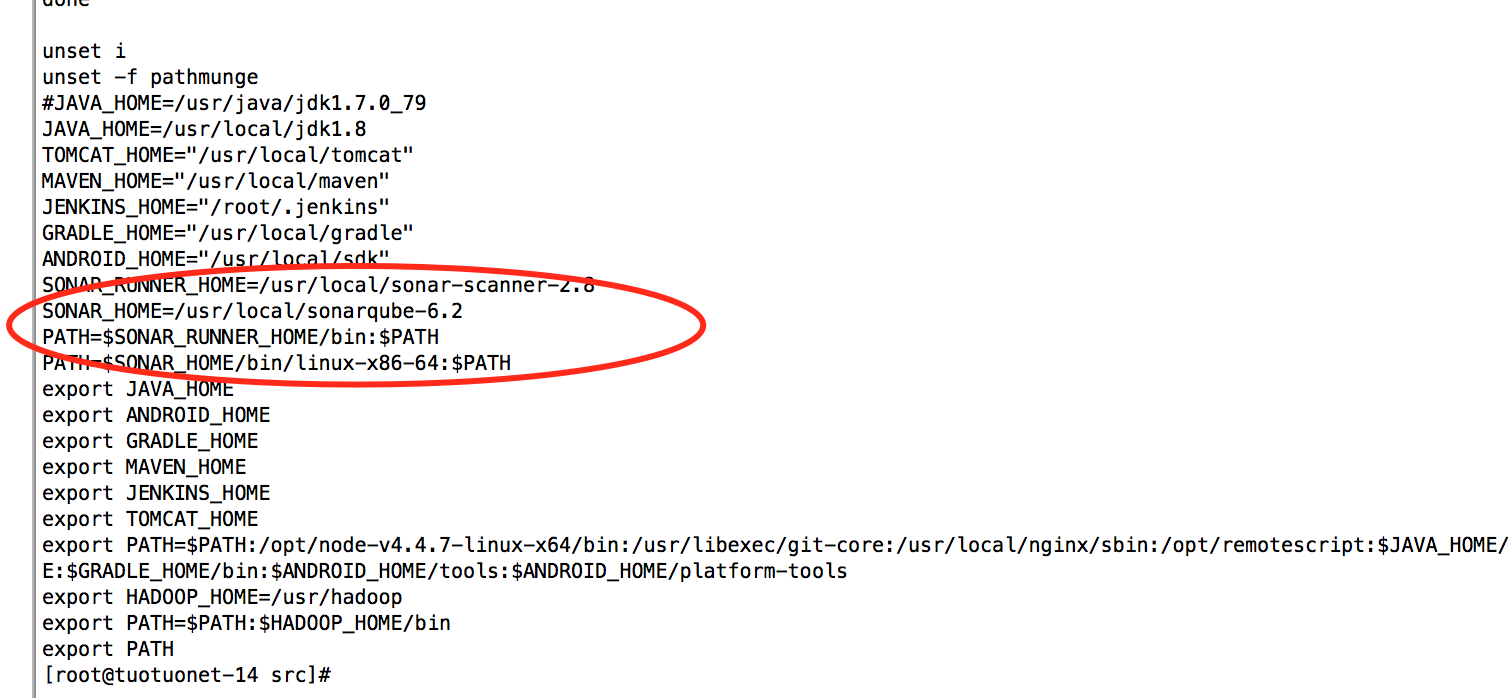
设置环境变量

[root@tuotuonet-14 src]# vi /etc/profile

 

##【验证】测试SonarJava:

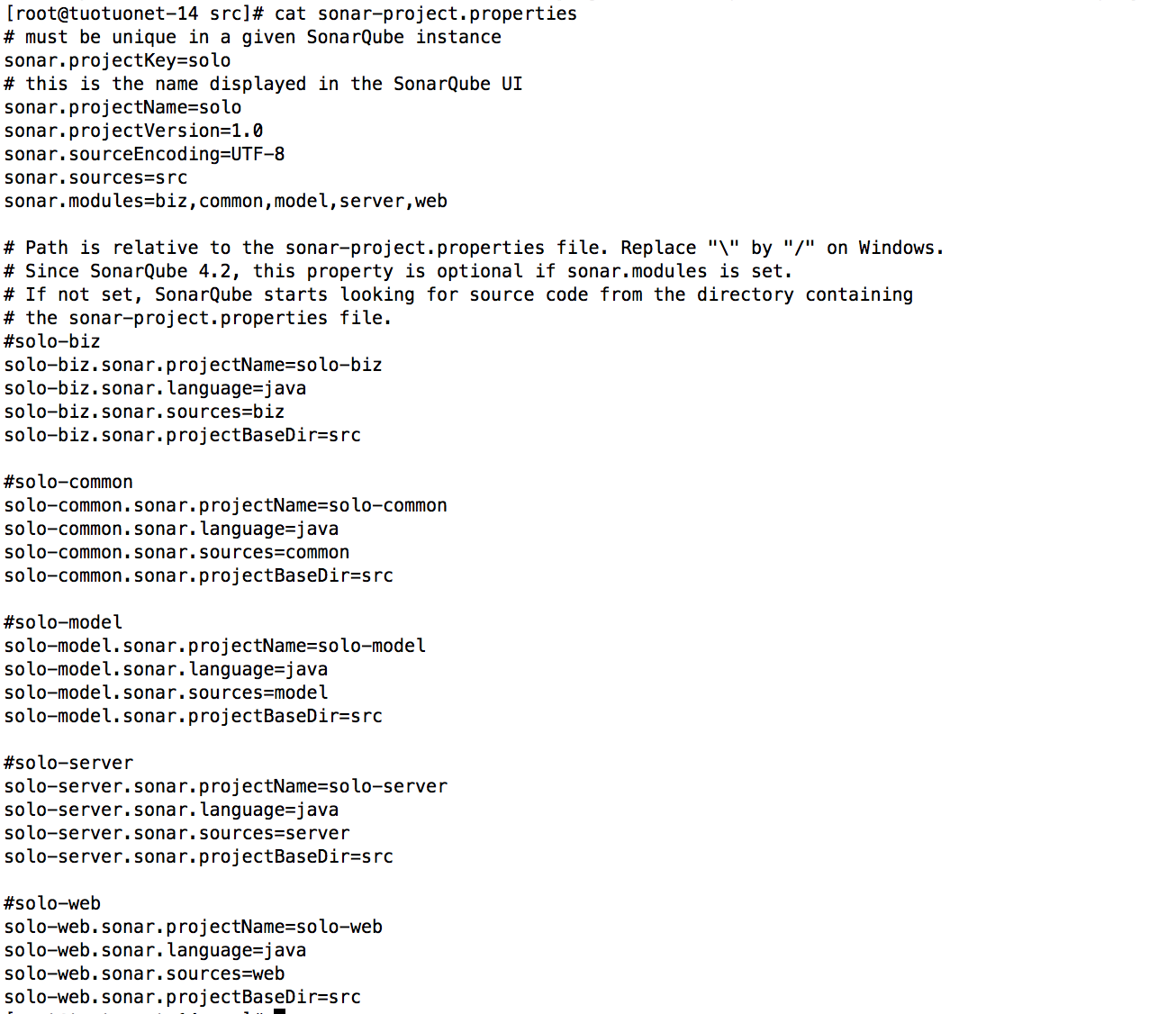
1.下载solo-server项目, 在根目录中新建:

sonar-project.properties，以下配置针对多项目结构的工程

 

2.开始分析

输入: sonar-scanner

3.结果展示

 

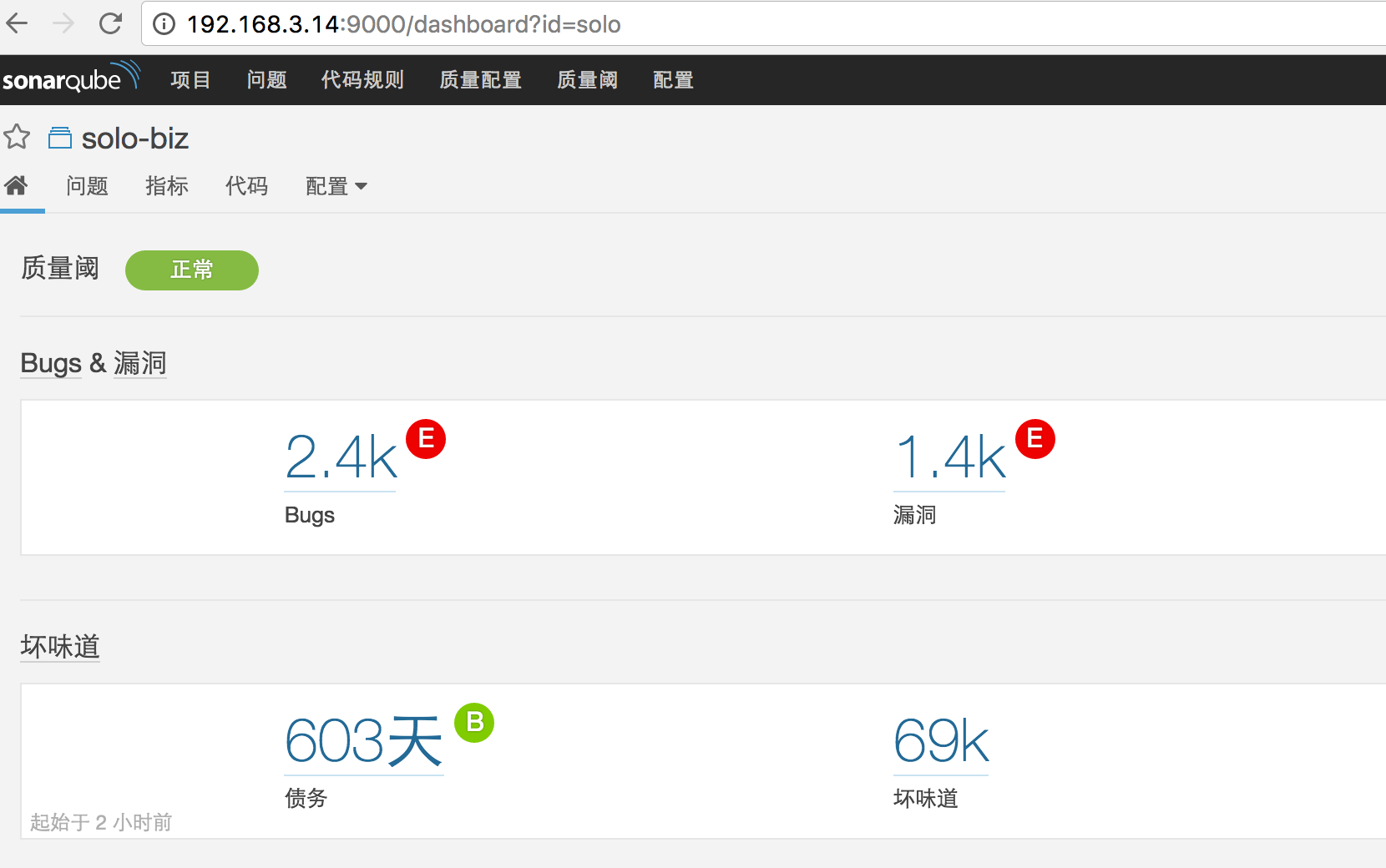
[自定义]插件导入:

1.打包插件:

打包命令: mvn clean && mvn package -Dmaven.test.skip=true

 

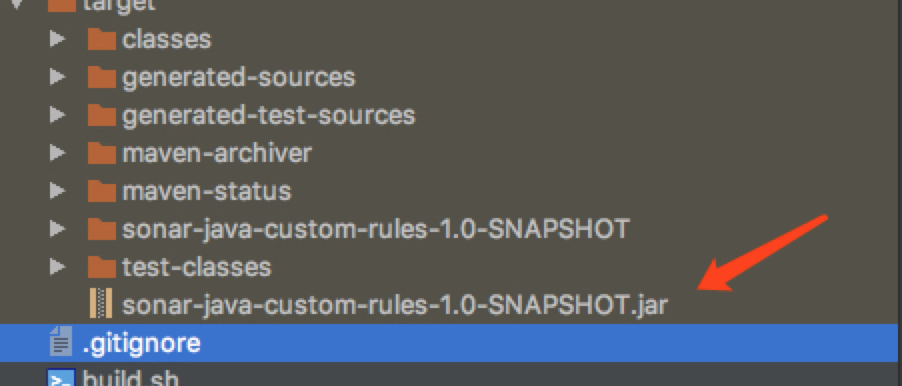
2.把jar放置到sonar插件目录:

 

3.重启sonar服务:sonar.sh restart

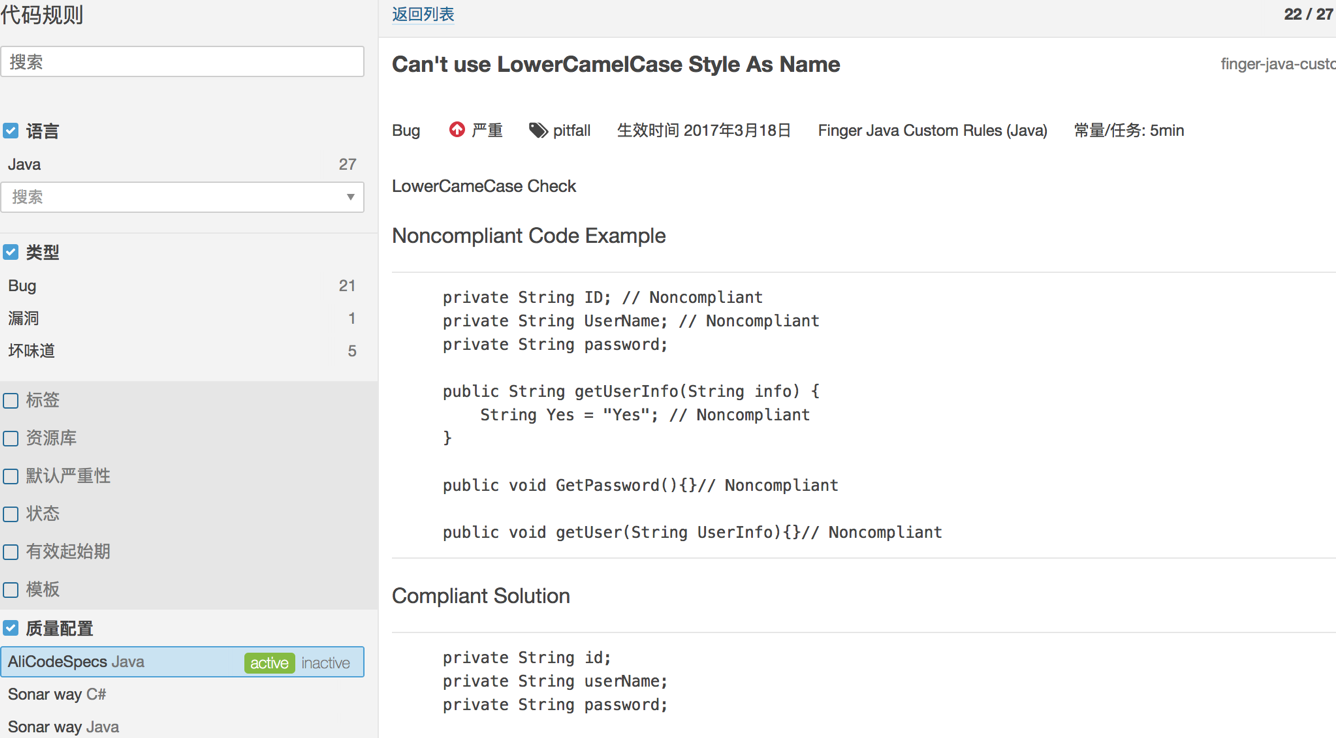
4.查看sonar质量规则，可以看到我们新增的插件规则:

 

 

 

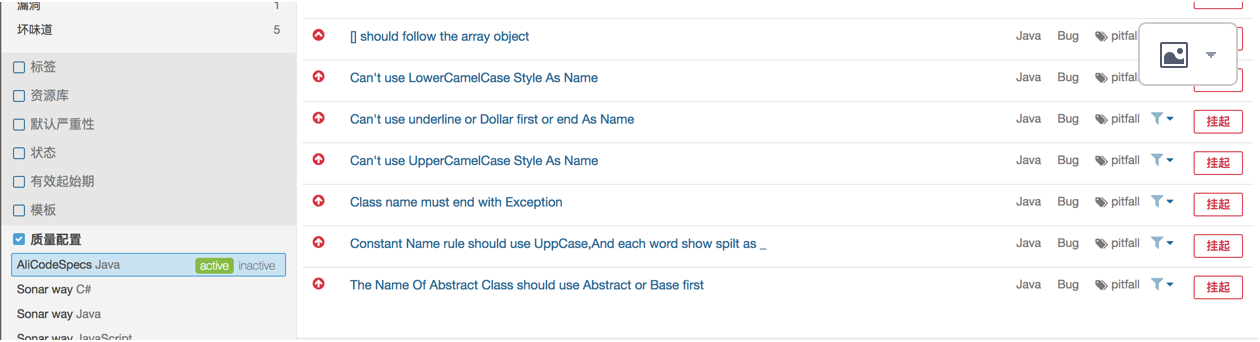
启动服务:[root@tuotuonet-14 src]# sonar.sh start | stop | restart