TSP 遗传算法

GA——遗传算法

同模拟退火算法一样，都是现代优化算法之一。模拟退火是在一定接受程度的情况下仍然接受一个比较差的解。

遗传算法，是真真正正的和大自然的遗传进化有着非常紧密的联系的，当然遗传进化的只是在生物学中已经讲过了，8个字，物竞天择，适者生存。

• 简介

《物种起源》，有兴趣可以看看达尔文的著作。

物竞天择，适者生存，这两句话，也可以说是对遗传算法过程的伪代码描述了，物竞天择，就是我们的目标函数，只有越满足我们的目标函数的个体才会留下来，适者生存，就是我们在算法的过程中要淘汰一些个体。

• 基因编码方式

生物学里面告诉我们，遗传，变异都是以种群为研究对象的，怎么表示一个解呢？用他的基因表示，嘿嘿，组成这个解的步骤表示，第一步干什么，第二步干什么，怎么在程序中编码呢？

常用两种编码方式：二进制编码，浮点数编码。

二进制编码：一定精度的二进制只能表示一定精度的浮点数。栗子，要求精确到6位小数，而区间是 [-1,2]，至少要把区间划分为3*10^6等分。编码也就需要22位。这里就涉及到一个二进制串转换到一个区间为 [-1,2] 的实数，两者相互转换。比如得到的十进制数为 x，那么对应的 [-1,2] 区间的浮点数就是

 

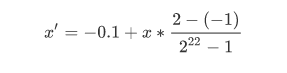
浮点数编码：为改善遗传算法的复杂度，提出来浮点数编码

• 适应评分及选择函数

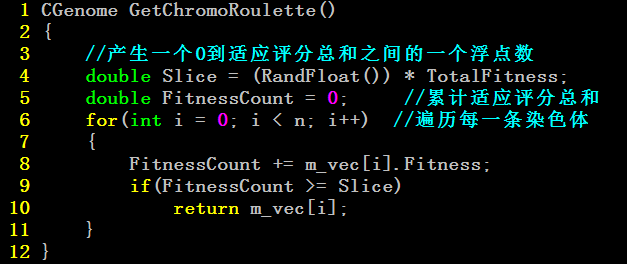
适应评分函数就是用来衡量哪个个体应该被淘汰。但是也不能说，取值差点的个体一定就被淘汰了，这里会有一个概率存在，怎么建立一种概率关系呢？常用的方法是轮盘法。假设种群数为 n，某个个体 i 的适应度为 fi，那么个体 i 被选择的概率是：

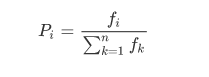
So，遗传算法中的自然选择过程：

适应评分函数——求出各个体的适应评分值

轮盘选择——个体被选择的概率

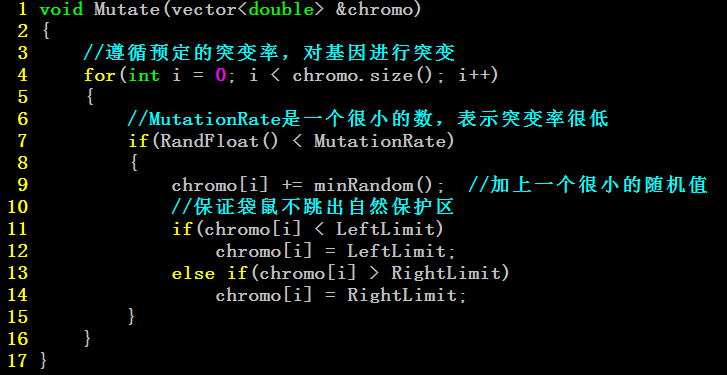
• 基因重组与基因突变

在生物学中，基因重组有两种情况。

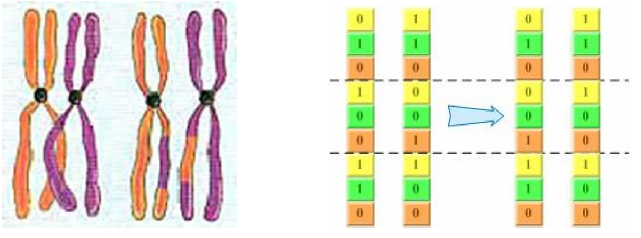
基因重组，就是两个个体基因发生交换。

基因突变是一种小概率事件。

使得一个基因变成他的等位基因，引起一定的表现型变化。

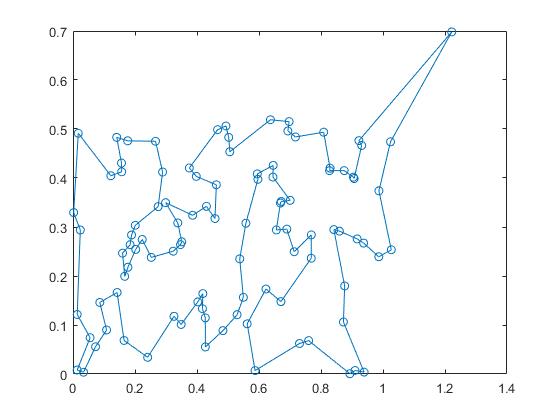
• TSP问题求解

TSP问题，之前已经用费用流，和模拟退火做过了，现在用遗传来讨论。

程序过程和自然界中的遗传与进化是一样的。

1. 生成50个个体，形成种群，并基因编码。

2. 基因重组，突变，和父代，一起进行天择。

3. 重复100次进化。得到较优的解。

clc,clear;
sj0 = load('sj.txt');
x = sj0(:,::); x = x(:);
y = sj0(:,::); y = y(:);
sj = [x,y];d1 = [,];
sj = [d1;sj;d1]; sj = sj*pi/;
​
d = zeros();
​
for i  = :
    for j = i+:
        d(i,j) = *acos(cos(sj(i,)-sj(j,))*cos(sj(i,))*cos(sj(j,))+sin(sj(i,))*sin(sj(j,)));
    end
end
​
d = d + d';
% w 为种群数,g为进化的代数
w = ;
g = ;
rand('state',sum(clock));
​
% 改良圈算法选取初始种群
for k=:w  %通过改良圈算法选取初始种群
    c=randperm(); %产生1，...，100的一个全排列
    c1=[,c+,]; %生成初始解
    for t=: %该层循环是修改圈
        flag=; %修改圈退出标志
        for m=:
            for n=m+:
                if d(c1(m),c1(n))+d(c1(m+),c1(n+))<d(c1(m),c1(m+))+d(c1(n),c1(n+))
                    c1(m+:n)=c1(n:-:m+);  flag=; %修改圈
                end
            end
        end
        if flag==
            J(k,c1)=:; break %记录下较好的解并退出当前层循环
        end
   end
end
​
% 染色体编码
J(:,) = ;
J = J/;
​
% 100次进化
for k = :g
    A = J;
    c = randperm(w);
    for i = ::w                       % 基因重组
        F =  + floor(*rand());     % 产生交叉操作的染色体对
        tmp = A(c(i),[F:]);
        A(c(i),[F:]) = A(c(i+),[F:]);
        A(c(i+),F:) = tmp;
    end
​
    % 变异
    by = [];
    while ~isempty(by)      % 变异的个体数也是随机的
        by =find(rand(,w)<0.1);
    end

    B = A(by,:);        % 变异染色体
    for j = :length(by)
        bw = sort(+floor(*rand(,)));      % 产生变异操作的3个地址
        B(j,:) = B(j,[:bw(),bw()+:bw(),bw():bw(),bw()+:]);

    end

    G=[J;A;B];       % 父代和子代
    % 基因翻译为解空间,把染色体翻译成1,...,102的序列ind1
    [SG,ind1] = sort(G,);
    num = size(G,);        % 父子种群的总个体数
    long = zeros(,num);

    % 每一个体的优劣
    for j = :num
        for i = :
            long(j) = long(j)+d(ind1(j,i),ind1(j,i+));
        end
    end

    [slong,ind2] = sort(long);
    J = G(ind2(:w),:);
end
​
path = ind1(ind2(),:);
flong = slong();
xx = sj(path,);
yy = sj(path,);
plot(xx,yy,'-o');

参考：

ACdreamer

司守奎