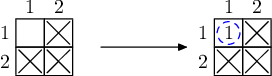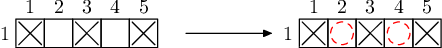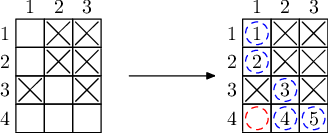CF1012B Chemical table 题解【二分图】【构造】
有意思的网格图转化。CF Div.1 还是挺有难度的。
注:由于本题有较完美的中文题面,所以不贴英文题面。
英文题面
题目描述
Innopolis 大学的教授正努力研究元素周期表。他们知道,有 \(n \times m\) 种元素,形成了一个 \(n\) 行 \(m\) 列的矩阵。
研究表明,如果元素周期表上有一个元素 A,且元素 B 与它在同一列(A 与 B 不能在同一周期),元素 C 在同一周期(A 与 C 不能在同一列),那么,科学家就可以用这三种元素通过核聚变合成第四种元素 D 的样品,D 与 B 在同一周期,与 C 在同一列。
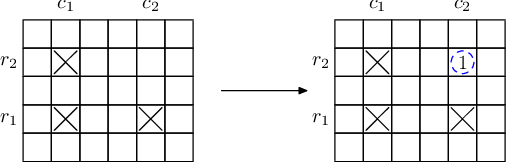
简而言之,如果有在元素周期表中位置为 \((r_1, c_1),\ (r_1, c_2),\ (r_2, c_1)\) (其中 \(r_1\ne r_2,c_1\ne c_2\))的三种元素的样品,就可以生成位置为 \((r_2, c_2)\)) 的样品。如图所示:
注意:在核聚变中被使用的样品并不会消失,它们可以参与之后的反应;反应得到的样品也可以参与反应。
他们已经获得了 \(q\) 种元素的样品。为了集齐所有元素的样品,他们会购买一些样品,然后利用核聚变制造出剩下元素的样品。
请求出他们至少需要购买的元素样品的数量。
输入输出格式
输入格式:
第一行,\(3\) 个整数 \(n,m,q\ (1\le n,m\le 2\times 10^5, 0\le q\le\min \{n \times m, 2 \times 10^5\})\)。
之后的 \(q\) 行,每行 \(2\) 个整数 \(r_i, c_i\ (1\le r_i\le n,1\le c_i\le m)\)。保证给定的元素互不相同。
输出格式:
输出一个整数,表示至少需要购买的元素样品的数量。
输入输出样例
输入样例#1:
2 2 3
1 2
2 2
2 1
输出样例#1:
0
输入样例#2:
1 5 3
1 3
1 1
1 5
输出样例#2:
2
输入样例#3:
4 3 6
1 2
1 3
2 2
2 3
3 1
3 3
输出样例#3:
1
样例解释
说明
每个样例解释中有两个矩阵。
第一个表示初始状况(其中,打叉的是原本就有样品的元素)。
第二个表示最终集齐样品时的状况(其中,蓝圈代表核聚变得到的样品,蓝圈中的数字表示得到样品的顺序,红圈表示购买的样品)。样例解释 1
通过给定的三种元素,可以得到第四种元素的样品。
样例解释 2
由于给定的元素只有一行,无法使用核聚变,只能购买剩余的两种元素的样品。
样例解释 3
集齐所有元素的方法不唯一,以下是一种方法。其中,元素 \((4,2)\) 只有在购买元素 \((4,1)\) 的样品,和反应得到元素 \((1,1)\) 的样品后才能得到。
子任务
注意:当且仅当你通过了一个子任务下的所有测试点,你将获得此子任务的分数。
子任务编号 分数 \(n\) \(m\) \(q\) \(1\) \(10\) \(n=2\) \(m=2\) \(0\le q\le 4\) \(2\) \(17\) \(1 \le n \le 2\) \(1 \le m \le 20\) \(0 \le q \le 20\) \(3\) \(8\) \(1 \le n \le 20\) \(1 \le m \le 20\) \(q=0\) \(4\) \(20\) \(1 \le n \le 20\) \(1 \le m \le 20\) \(0\le q \le 400\) \(5\) \(30\) \(1 \le n \le 1 \times 10^4\) \(1 \le m \le 1 \times 10^4\) \(1 \le q \le 1 \times 10^5\) \(6\) \(15\) \(1 \le n \le 2 \times 10^5\) \(1 \le m \le 2 \times 10^5\) \(1 \le q \le 2 \times 10^5\)
题解:
一开始总在找规律,比如先放没放过的行或列,先把给出的元素全部聚变一遍……
实际上在这个网格图中,我们把每行、每列均抽象为一个点,可以看成是一个二分图,每个点连接了它的行和列。
那么当一对行、列连通而它们之间又没有直接连边时,可以通过它的路径生成同时在这一行且在这一列的那个点。因此不需要直接连边。
那么我们计算把整个二分图连通需要多少条边,就是连通块个数-1。
Code:
#include<cstdio>
#include<cstring>
struct edge
{
int n,nxt;
edge(int n,int nxt)
{
this->n=n;
this->nxt=nxt;
}
edge(){}
}e[400100];
int head[400100],ecnt=-1;
void add(int from,int to)
{
e[++ecnt]=edge(to,head[from]);
head[from]=ecnt;
e[++ecnt]=edge(from,head[to]);
head[to]=ecnt;
}
bool used[400100];
int dfs(int x)
{
used[x]=1;
for(int i=head[x];~i;i=e[i].nxt)
if(!used[e[i].n])
dfs(e[i].n);
return 1;
}
int main()
{
memset(head,-1,sizeof(head));
int n,m,k,u,v;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=k;++i)
{
scanf("%d%d",&u,&v);
add(u,n+v);
}
int ans=0;
for(int i=1;i<=n+m;++i)
if(!used[i])
ans+=dfs(i);
printf("%d\n",ans-1);
return 0;
}
CF1012B Chemical table 题解【二分图】【构造】的更多相关文章
- CF1012B Chemical table
$CF1012B Chemical table 给你一个 \(n\times m\) 的矩形,一开始有 \(q\) 个格子上被标记.对于任意两行两列,如果交汇的四个格子中有三个被标记,那么第 \(4\ ...
- CF1012B Chemical table(构造)
[Luogu-CF1012B] 还有重题 P5089[eJOI2018]元素周期表 题解原话 : 可以发现这个过程是不改变二分图中的连通分量的个数的 答案就是 连通分量数-1 证明 : 设一行或一列为 ...
- CF1012B Chemical table 构造_思维_并查集
我们可以将横坐标和纵坐标看成是点.发现这些点之间是有传递性的. 题中说明,如果有矩阵中三个顶点被选,则底角的点也会被覆盖,发现这些点之间是有传递性的.那么我们最终达到的目的就是使整个图中只有 111 ...
- Codeforces 1012B Chemical table (思维+二分图)
<题目链接> 题目大意:给定一个n*m的矩阵网格,向其中加点,对于一个组成矩形的四个点中如果有三个点中有元素,那么第四个点中会自动产生新的元素.问你最少再加多少个点能够填满这个网格.解题分 ...
- 【题解】CF742E (二分图+构造)
[题解]CF742E (二分图+构造) 自闭了CodeForces - 742E 给定的条件就是一个二分图的模型,但是有一些不同.不同就不同在可以出现相邻两个点颜色相同的情况. 构造常用方法之一是按奇 ...
- 洛谷 P5089: CodeForces #500 (Div. 1) B / 1012B : Chemical table
题目传送门:洛谷P5089. 题意简述: 一张 \(n \times m\) 的表格,有一些格子有标记,另外一些格子没有标记. 如果 \((r_1,c_1),(r_1,c_2),(r_2,c_1)\) ...
- UVALive 3523 : Knights of the Round Table (二分图+BCC)
题目链接 题意及题解参见lrj训练指南 #include<bits/stdc++.h> using namespace std; ; int n,m; int dfn[maxn],low[ ...
- cf623A. Graph and String(二分图 构造)
题意 题目链接 Sol 可以这样考虑,在原图中没有边相连的点的值肯定是a / c 那么直接二分图染色即可 #include<bits/stdc++.h> #define LL long l ...
- POJ2942:Knights of the Round Table——题解
http://poj.org/problem?id=2942 所写的tarjan练习题最难的一道. 说白了难在考得不是纯tarjan. 首先我们把仇恨关系处理成非仇恨关系的图,然后找双连通分量,在双连 ...
随机推荐
- 修改apache的默认访问路径
- 一起做RGB-D SLAM (3)
第三讲 特征提取与配准 2016.11 更新 把原文的SIFT替换成了ORB,这样你可以在没有nonfree模块下使用本程序了. OpenCV可以使用 apt-get install libopenc ...
- 二项分布&超几何分布
伯努利分布 在一次试验中,事件A出现的概率为p,不出现的概率为q=1-p.若以β记事件A出现的次数,则β仅取0,1两值,相应的概率分布为: 二项分布是指在只有两个结果的n次独立的伯努利试验中,所期望 ...
- python 输入输出,file, os模块
Python 输入和输出 输出格式美化 Python两种输出值的方式: 表达式语句和 print() 函数. 第三种方式是使用文件对象的 write() 方法,标准输出文件可以用 sys.stdout ...
- cookie与session组件
会话跟跟踪技术 cookie介绍 Djanjo中操作Cookle Session Django中Session相关方法 Django中的Session配置 CBV中加装饰器 session中运用aja ...
- Vmware下CentOs7 桥接模式下配置固定IP
1.安装完CentOS7后 修改虚拟机网络适配器配置:改成桥接模式 2.设置Vmware的 编辑->虚拟网络编辑器 3.重启CentOs7 , 查看网络 # ip addr interface是 ...
- JavaEE互联网轻量级框架整合开发(书籍)阅读笔记(10):通过注解(annotation)装配Bean之(@Configguration、@Component、@Value、@ComponentScan、@Autowired、@Primary、@Qualifier、@Bean)
一.通过注解(annotation)装配Bean 通过之前的学习,我们已经知道如何使用XML装配Bean,但是更多的时候已经不再推荐使用XML的方式去装配Bean,更多的时候会考虑注解(annotat ...
- Understanding sun.misc.Unsafe
转自: https://dzone.com/articles/understanding-sunmiscunsafe The biggest competitor to the Java virtua ...
- asp.net WebAPI 问题 iisnode默认不支持PUT和DELETE的解决
因为iisnode的自动重启服务器方便,一直用的它来作为开发中的node服务器,今天一个delete命令过去,得到一个405(?好像是)错误,让我很郁闷. 用原生的node试一下,是完美支持的,本来打 ...
- win10登录不上sql2005
因需求安装了一个SQL Server 2005. 登录的时候,用户Sa模式可以登录,Windows身份验证方式却无法登录. 经测试.解决方法如下: SQL Server Management Stud ...