[吴恩达机器学习笔记]14降维5-7重建压缩表示/主成分数量选取/PCA应用误区

14.降维

觉得有用的话,欢迎一起讨论相互学习~Follow Me

14.5重建压缩表示 Reconstruction from Compressed Representation

• 使用PCA，可以把 1000 维的数据压缩到100 维特征，或将三维数据压缩到一二维表示。所以，如果如果把PCA任务是一个压缩算法，应该能回到这个压缩表示之前的形式，回到原有的高维数据的一种近似。下图是使用PCA将样本\(x^{(i)}映射到z^{(i)}\)上
  
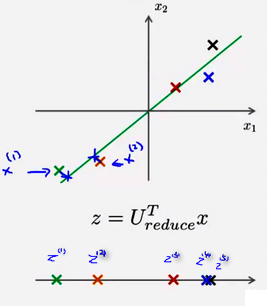
  即是否能通过某种方法将z上的点重新恢复成使用\(x_{(1)}和x_{(2)}\)二维方式表示的数据。

  方法

• 使用\(X_{appox}\)表示重建样本的n维向量(n * 1)，使用\(U_{reduce}\)表示使用PCA算法时选取的K个特征向量组成的特征矩阵(n * k)，使用\(Z\)表示使用PCA降维后数据样本的新特征(k * 1).有：\[X_{appox}=U_{reduce} * Z\] 即
  

---

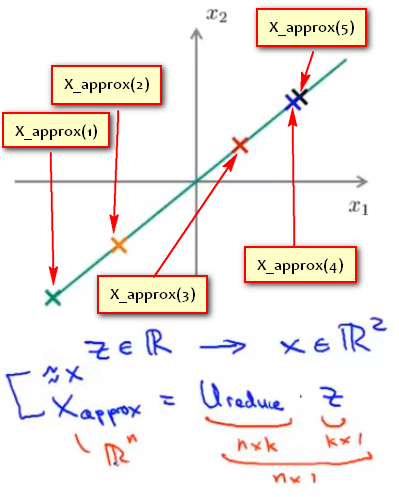
14.6主成分数量的选取 Choosing the number of pricipal components

平均平方映射误差(Average Squared Projection Error)和总变差(Total Variation)

• PCA的目的是减少 平均平方映射误差 ，，即是要减少 原始样本\(x^{(i)}\) 和 通过重建后的样本\(x_{appox}^{(i)}\)(低维映射点) 的平方差的平均值
  \[\frac{1}{m}\sum^{m}_{i=1}||x^{(i)}-x_{appox}^{(i)}||^{2}\]

• 数据的总变差(Total Variation)：定义为原始数据样本的长度的均值:\[\frac{1}{m}\sum^{m}_{i=1}||x^{(i)}||^{2}\] 意为：平均来看原始数据距离零向量的距离。

  K值选择的经验法则

• 在 平均平方映射误差 和 总变差 的比值尽可能小的情况下 (一般选择0.01) 选择尽可能小的K值, 对于此比例小于0.01，专业来说：保留了数据99%的差异性(99% of variance is retained)
  

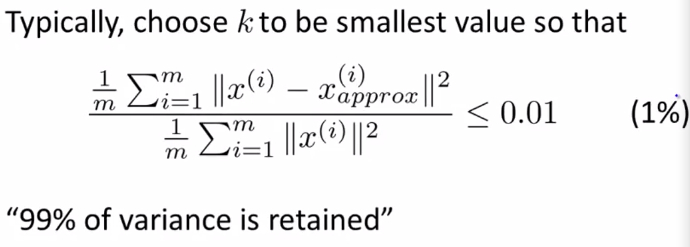
  选择了参数K，并且99%的差异性得以保留

• 常用的其他数值也有 0.05和0.10，则95%和90%的差异性得以保留。

  主成分数量选择算法

  效率较低的方法

  先令 K=1，然后进行主要成分分析，获得 \(U_reduce\) 和\(z^{(1)},z^(2),...z^{(m)}\),然后计算其低维映射点\(x_{appox}^{(i)}\),然后计算 平均平方映射误差 和 总变差 的比值是否小于1%。如果不是的话再令 K=2，如此类推，直到找到可以使得比例小于 1%的 最小K值
  

  更好的方法

• 还有一些更好的方式来选择 K，当计算协方差矩阵sigma，调用“svd”函数的时候，我们获得三个参数：\[[U, S, V] = svd(sigma)\] ,其中U是特征向量,而S是一个对角矩阵，对角线的元素为 \(S_{11},S_{22},S_{33}...S_{nn}\) 而矩阵的其余元素都是0。
  

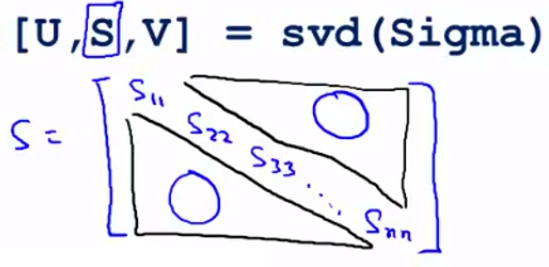
• 可以证明的是(在此只说明公式不给出证明过程)，以下两个式子相等，即：
  
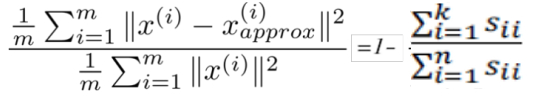
  所以，原有的条件可以转化为：
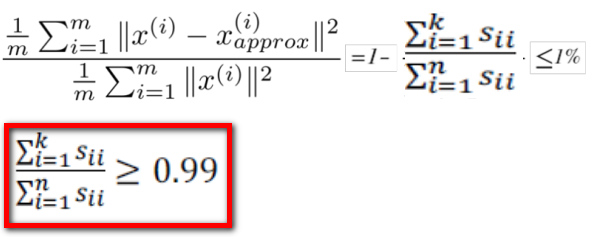  根据上式找出满足条件的最小的K值即可。

---

14.7 主成分分析法的应用建议

测试集和验证集应使用和训练集一样的特征向量\(U_{reduce}\)

• 假使我们正在针对一张 100×100 像素的图片进行某个计算机视觉的机器学习，即总共有 10000 个特征。

1. 第一步是运用主要成分分析将数据压缩至 1000 个特征
2. 然后对训练集运行学习算法
3. 在预测时，采用训练集上学习而来的 \(U_{reduce}\) 将输入的特征 x 转换成特征向量 z，然后再进行预测

• Note 如果我们有交叉验证集合测试集，也采用对训练集学习而来的 \(U_{reduce}\)

  PCA不是用于解决过拟合的方法

• 一个常见错误使用主要成分分析的情况是，将PCA用于减少过拟合（通过减少特征的数量）。这样做 非常不好，应该使用正则化化处理。原因在于主要成分分析只是近似地丢弃掉一些特征，它并不考虑任何与 结果变量y(即预测的标签) 有关的信息，因此可能会丢失非常重要的特征。PCA毕竟无监督学习的方法，任何的特征，无论是输入属性还是标签属性，其都一样对待，没有考虑到输入信息的减少对标签y的影响，通过PCA舍弃掉一部分输入属性却没有对标签做任何补偿。 然而当我们进行正则化化处理时，由于逻辑回归或者神经网络或者SVM会考虑到正则化及输入属性的改变对结果变量(预测标签)的影响，并对其作出反馈，所以正则化不会丢掉重要的数据特征。

  PCA不是必要的方法

• PCA是当数据量大，所以要 压缩数据维度，减少数据占用内存，加快训练速度 时使用的，或者是需要通过 数据可视化 理解数据时使用的， 而 不是一种必需的方法。默认把PCA加入到机器学习系统中而不考虑不加入PCA时系统的表现是不对的。由于PCA会损失掉一部分数据，也许正是数据中十分关键的维度 ，所以机器学习系统应当首先 不考虑PCA的使用 ，而使用常规的训练方法， 只在有必要的时候（算法运行太慢或者占用太多内存） 才考虑采用主要成分分析。