Hdu1828 Picture

Picture

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5516    Accepted Submission(s): 2636

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

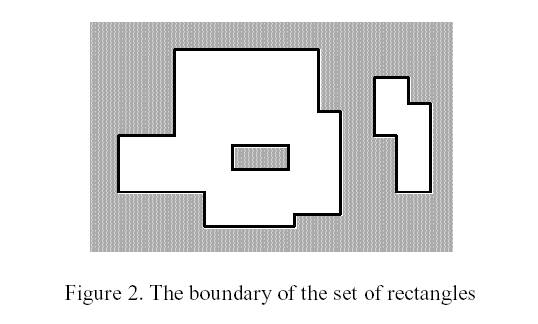
The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

 

Sample Output

228

 

Source

IOI 1998

题目大意：求矩形的周长.

分析：还是线段树+扫描线法.从下往上扫竖线，记录一个类似前缀和一样的东西，表示已经扫过的总长度，扫完当前层后的总长度-以前扫过的总长度的绝对值就是横线的答案.那纵线怎么求呢？采用与求面积差不多的方法，往上跳.跳到最近的上面的横线，那么当前有num条横线就能向上跳num*2*h长度的竖线.因为一条竖线两个端点.竖线答案+横线答案就是问题的解.

          比较容易出错的是最后竖线还要往上跳一次，所以要加一个哨兵元素.

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = , inf = 0x7ffffff;
int n, ans, cnt, minn = inf, maxx = -inf, tot;
int L[maxn << ], R[maxn << ], c[maxn << ], lc[maxn << ], rc[maxn << ], num[maxn << ], tag[maxn << ];

struct node
{
    int l, r, h, id;
}e[maxn * ];

void build(int o, int l, int r)
{
    L[o] = l;
    R[o] = r;
    num[o] = ;
    lc[o] = rc[o] = ;
    c[o] = ;
    if (l == r)
        return;
    int mid = (l + r) >> ;
    build(o * , l, mid);
    build(o *  + , mid + , r);
}

bool cmp(node a, node b)
{
    return a.h < b.h;
}

void pushup(int o)
{
    int l = L[o], r = R[o];
    if (tag[o])
    {
        c[o] = r - l + ;
        lc[o] = rc[o] = ;
        num[o] = ;
    }
    else
        if (l == r)
        {
            c[o] = ;
            num[o] = ;
            lc[o] = rc[o] = ;
        }
        else
        {
            c[o] = c[o * ] + c[o *  + ];
            lc[o] = lc[o * ];
            rc[o] = rc[o *  + ];
            num[o] = num[o * ] + num[o *  + ] - (rc[o * ] & lc[o *  + ]);
        }
}

void update(int o, int x, int y, int v)
{
    int l = L[o], r = R[o];
    if (x <= l && r <= y)
    {
        tag[o] += v;
        pushup(o);
        return;
    }
    int mid = (l + r) >> ;
    if (x <= mid)
        update(o * , x, y, v);
    if (y > mid)
        update(o *  + , x, y, v);
    pushup(o);
}

int main()
{
    while (scanf("%d", &n) != EOF)
    {
        if (n == )
        {
            printf("%d\n", );
            continue;
        }
        tot = ans = cnt = ;
        minn = inf;
        maxx = -inf;
        memset(c, , sizeof(c));
        memset(num, , sizeof(num));
        memset(tag, , sizeof(tag));
        memset(lc, , sizeof(lc));
        memset(rc, , sizeof(rc));
        memset(L, , sizeof(L));
        memset(R, , sizeof(R));
        for (int i = ; i <= n; i++)
        {
            int a, b, c, d;
            scanf("%d%d%d%d", &a, &b, &c, &d);
            minn = min(a, minn);
            maxx = max(c, maxx);
            e[++tot].l = a;
            e[tot].r = c;
            e[tot].h = b;
            e[tot].id = ;
            e[++tot].l = a;
            e[tot].r = c;
            e[tot].h = d;
            e[tot].id = -;
        }
        sort(e + , e +  + tot, cmp);
        build(, minn, maxx - );
        int last = ;
        e[tot + ].h = e[tot].h;
        for (int i = ; i <= tot; i++)
        {
            update(, e[i].l, e[i].r - , e[i].id);
            ans += abs(c[] - last);
            ans += (e[i + ].h - e[i].h) * num[] * ;
            last = c[];
        }
        printf("%d\n", ans);
    }

    return ;
}