POJ 1410 Intersection（判断线段交和点在矩形内）

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9996		Accepted: 2632

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
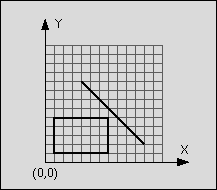
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

Source

Southwestern European Regional Contest 1995

 

 

 

给了一个线段和矩形。

 

如果线段和矩形的边相交，或者线段在矩形内。输出T

否则输出F

 

/************************************************************
 * Author        : kuangbin
 * Email         : kuangbin2009@126.com
 * Last modified : 2013-07-15 10:14
 * Filename      : POJ1410Intersection.cpp
 * Description   :
 * *********************************************************/

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <map>
#include <vector>
#include <set>
#include <string>
#include <math.h>

using namespace std;

const double eps = 1e-;
int sgn(double x)
{
    if(fabs(x) < eps)return ;
    if(x < )return -;
    else return ;
}
struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y)
    {
        x = _x;y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    //叉积
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    //点积
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    //绕原点旋转角度B（弧度值），后x,y的变化
    void transXY(double B)
    {
        double tx = x,ty = y;
        x = tx*cos(B) - ty*sin(B);
        y = tx*sin(B) + ty*cos(B);
    }
};
struct Line
{
    Point s,e;
    Line(){}
    Line(Point _s,Point _e)
    {
        s = _s;e = _e;
    }
    //两直线相交求交点
    //第一个值为0表示直线重合，为1表示平行，为0表示相交,为2是相交
    //只有第一个值为2时，交点才有意义
    pair<int,Point> operator &(const Line &b)const
    {
        Point res = s;
        if(sgn((s-e)^(b.s-b.e)) == )
        {
            if(sgn((s-b.e)^(b.s-b.e)) == )
                return make_pair(,res);//重合
            else return make_pair(,res);//平行
        }
        double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));
        res.x += (e.x-s.x)*t;
        res.y += (e.y-s.y)*t;
        return make_pair(,res);
    }
};

//判断线段相交
bool inter(Line l1,Line l2)
{
    return
    max(l1.s.x,l1.e.x) >= min(l2.s.x,l2.e.x) &&
    max(l2.s.x,l2.e.x) >= min(l1.s.x,l1.e.x) &&
    max(l1.s.y,l1.e.y) >= min(l2.s.y,l2.e.y) &&
    max(l2.s.y,l2.e.y) >= min(l1.s.y,l1.e.y) &&
    sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s-l1.e)) <=  &&
    sgn((l1.s-l2.e)^(l2.s-l2.e))*sgn((l1.e-l2.e)^(l2.s-l2.e)) <= ;
}

//判断点在线段上
//判断点在线段上
bool OnSeg(Point P,Line L)
{
    return
    sgn((L.s-P)^(L.e-P)) ==  &&
    sgn((P.x - L.s.x) * (P.x - L.e.x)) <=  &&
    sgn((P.y - L.s.y) * (P.y - L.e.y)) <= ;
}
//判断点在凸多边形内
//点形成一个凸包，而且按逆时针排序（如果是顺时针把里面的<0改为>0）
//点的编号:0~n-1
//返回值：
//-1:点在凸多边形外
//0:点在凸多边形边界上
//1:点在凸多边形内
int inConvexPoly(Point a,Point p[],int n)
{
    for(int i = ;i < n;i++)
    {
        if(sgn((p[i]-a)^(p[(i+)%n]-a)) < )return -;
        else if(OnSeg(a,Line(p[i],p[(i+)%n])))return ;
    }
    return ;
}
//判断点在任意多边形内
//射线法，poly[]的顶点数要大于等于3,点的编号0~n-1
//返回值
//-1:点在凸多边形外
//0:点在凸多边形边界上
//1:点在凸多边形内
int inPoly(Point p,Point poly[],int n)
{
    int cnt;
    Line ray,side;
    cnt = ;
    ray.s = p;
    ray.e.y = p.y;
    ray.e.x = -100000000000.0;//-INF,注意取值防止越界

    for(int i = ;i < n;i++)
    {
        side.s = poly[i];
        side.e = poly[(i+)%n];

        if(OnSeg(p,side))return ;

        //如果平行轴则不考虑
        if(sgn(side.s.y - side.e.y) == )
            continue;

        if(OnSeg(side.s,ray))
        {
            if(sgn(side.s.y - side.e.y) > )cnt++;
        }
        else if(OnSeg(side.e,ray))
        {
            if(sgn(side.e.y - side.s.y) > )cnt++;
        }
        else if(inter(ray,side))
            cnt++;
    }
    if(cnt %  == )return ;
    else return -;
}
int main()
{
    int T;
    double x1,y1,x2,y2;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
        Line line = Line(Point(x1,y1),Point(x2,y2));
        scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
        if(x1 > x2)swap(x1,x2);
        if(y1 > y2)swap(y1,y2);
        Point p[];
        p[] = Point(x1,y1);
        p[] = Point(x2,y1);
        p[] = Point(x2,y2);
        p[] = Point(x1,y2);
        if(inter(line,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        if(inter(line,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        if(inter(line,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        if(inter(line,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        if(inConvexPoly(line.s,p,) >=  || inConvexPoly(line.e,p,) >= )
        {
            printf("T\n");
            continue;
        }
        printf("F\n");
    }
    return ;
}