高斯混合模型参数估计的EM算法

介绍摘自李航《统计学习方法》

EM算法

EM算法是一种迭代算法，1977年由Dempster等人总结提出，用于含有隐变量（hidden variable）的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由两步组成：E步，求期望（expectation）；M步，求极大（maximization）。所以这一算法称为期望极大算法（expectation maximization algorithm），简称EM算法。本章首先叙述EM算法，然后讨论EM算法的收敛性；作为EM算法的应用，介绍高斯混合模型的学习；最后叙述EM算法的推广——GEM算法。

将观测数据表示为Y＝(Y₁，Y₂,…,Y_n)^T，未观测数据表示为Z＝(Z₁,Z₂,…,Z_n)^T，则观测数据的似然函数为

即

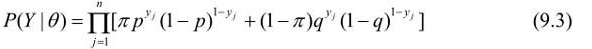
考虑求模型参数＝(Π,p,q)的极大似然估计，即

这个问题没有解析解，只有通过迭代的方法求解。EM算法就是可以用于求解这个问题的一种迭代算法。下面给出针对以上问题的EM算法，其推导过程省略。

EM算法首先选取参数的初值，记作⁽⁰⁾＝(Π⁽⁰⁾,p⁽⁰⁾,q⁽⁰⁾)，然后通过下面的步骤迭代计算参数的估计值，直至收敛为止。第i次迭代参数的估计值为⁽ⁱ⁾＝(⁽ⁱ⁾,p⁽ⁱ⁾,q⁽ⁱ⁾)。EM算法的第i+1次迭代如下。

E步：计算在模型参数Π⁽ⁱ⁾，p⁽ⁱ⁾，q⁽ⁱ⁾下观测数据y_j来自掷硬币B的概率

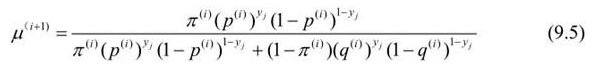
M步：计算模型参数的新估计值

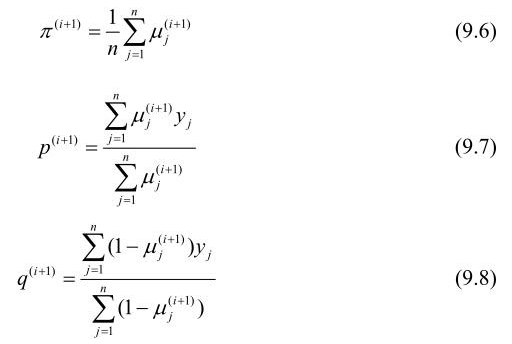
EM算法在高斯混合模型学习中的应用

EM算法的一个重要应用是高斯混合模型的参数估计。高斯混合模型应用广泛，在许多情况下，EM算法是学习高斯混合模型（Gaussian misture model）的有效方法。

定义9.2（高斯混合模型）　高斯混合模型是指具有如下形式的概率分布模型：

高斯混合模型参数估计的EM算法

1．明确隐变量，写出完全数据的对数似然函数

可以设想观测数据y_j，j＝1,2,…,N，是这样产生的：首先依概率a_k选择第k个高斯分布分模型Ø(y|θ_k)；然后依第k个分模型的概率分布Ø(y|θ_k)生成观测数据y_j。这时观测数据y_j，j＝1,2,…,N，是已知的；反映观测数据y_j来自第k个分模型的数据是未知的，k＝1,2,…,K，以隐变量γ_jk表示，其定义如下：

有了观测数据y_j及未观测数据γ_jk，那么完全数据是

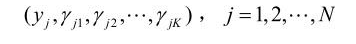
于是，可以写出完全数据的似然函数：

2．EM算法的E步：确定Q函数

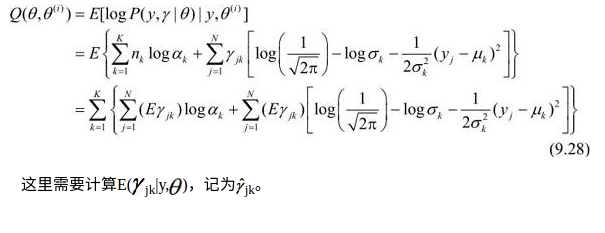
3．确定EM算法的M步

迭代的M步是求函数Q(θ,θ⁽ⁱ⁾)对的极大值，即求新一轮迭代的模型参数：

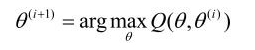
重复以上计算，直到对数似然函数值不再有明显的变化为止。

 # coding:utf-8
 import numpy as np

 def qq(y,alpha,mu,sigma,K,gama):#计算Q函数
     gsum=[]
     n=len(y)
     for k in range(K):
             gsum.append(np.sum([gama[j,k] for j in range(n)]))
     return np.sum([g*np.log(ak) for g,ak in zip(gsum,alpha)])+\
            np.sum([[np.sum(gama[j,k]*(np.log(1/np.sqrt(2*np.pi))-np.log(np.sqrt(sigma[k]))-1/2/sigma[k]*(y[j]-mu[k])**2))
                     for j in range(n)] for k in range(K)])  #《统计学习方法》中公式9.29有误

 def phi(mu,sigma,y): #计算phi
     return 1/(np.sqrt(2*np.pi*sigma)*np.exp(-(y-mu)**2/2/sigma))

 def gama(alpha,mu,sigma,i,k): #计算gama
     sumak=np.sum([[a*phi(m,s,i)] for a,m,s in zip(alpha,mu,sigma)])
     return alpha[k]*phi(mu[k],sigma[k],i)/sumak

 def dataN(length,k):#生成数据
     y=[np.random.normal(5*j,j+5,length/k) for j in range(k)]
     return y

 def EM(y,K,iter=1000): #EM算法
     n = len(y)
     sigma=[10]*K
     mu=range(K)
     alpha=np.ones(K)
     qqold,qqnew=0,0
     for it in range(iter):
         gama2=np.ones((n,K))
         for k in range(K):
             for i in range(n):
                 gama2[i,k]=gama(alpha,mu,sigma,y[i],k)
         for k in range(K):
             sum_gama=np.sum([gama2[j,k] for j in range(n)])
             mu[k]=np.sum([gama2[j,k]*y[j] for j in range(n)])/sum_gama
             sigma[k]=np.sum([gama2[j,k]*(y[j]-mu[k])**2 for j in range(n)])/sum_gama
             alpha[k]=sum_gama/n
         qqnew=qq(y,alpha,mu,sigma,K,gama2)
         if abs(qqold-qqnew)<0.000001:
             break
         qqold=qqnew
     return alpha,mu,sigma

 N = 500
 k=2
 data=dataN(N,k)
 y=np.reshape(data,(1,N))
 a,b,c = EM(y[0], k)
 print a,b,c
 # iter=180
 #[ 0.57217609  0.42782391] [4.1472879054766887, 0.72534713118155769] [44.114682884921415, 24.676116557533351]

 sigma = 6  #网上的数据
 miu1 = 40
 miu2 = 20
 X = np.zeros((1, N))
 for i in xrange(N):
     if np.random.random() > 0.5:
         X[0, i] = np.random.randn() * sigma + miu1
     else:
         X[0, i] = np.random.randn() * sigma + miu2
 a,b,c = EM(X[0], k)
 print a,b,c
 # iter=114
 #[ 0.44935959  0.55064041] [40.561782615819361, 21.444533254494189] [33.374144230703514, 51.459622219329155]