数据结构-二叉树（Binary Tree）

1、二叉树（Binary Tree）

是n（n>=0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根节点和两棵互不相交的，分别称为根节点的左子树和右子树的二叉树组成。

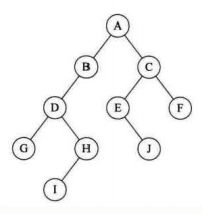
 2、特数二叉树

1)斜二叉树

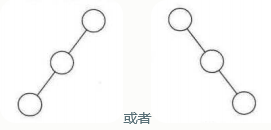
所有的结点都只有左子树的二叉树叫做左斜树

所有的结点都只有右子树的二叉树叫做右斜树

相当于链表，所以线性结构可以理解为是树的一种极其特殊的表现形式

2）满二叉树（完美二叉树）

所有分支结点都存在左子树和右子树。

所有叶子结点都在同一层

3）完全二叉树

对树按照上->下，左->右，编号为i的与满二叉树中为i的位置相同。

3、二叉树的重要性质

性质一：第i层最大结点数位2^(i-1)个，（i>=1）

性质二：深度为k的二叉树至多有2^k-1个结点

性质三：叶结点n0与度为2的结点n2的个数关系n0=n2+1

性质四：具有n个结点的完全二叉树的深度为[log2n]+1

性质五：对一棵有n个结点的完全二叉树，从第一层到最大层，对任一结点i(1=<i<=n)有：

注意：下标是从1开始的。

1.非根节点的父节点序号是[i/2]
2.结点（序号i）的左孩子为2i,若2i>n没有左孩子
3.结点（序号i）的右孩子为2i+1,若2i+1>n没有右孩子

但一般数组下标是从0开始的：

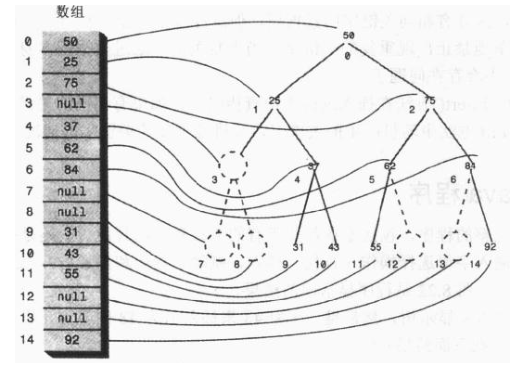
树中的每个位置，无论是否存在节点，都对应于数组中的一个位置，树中没有节点的在数组中用0或者null表示。

假设节点的索引值为index，那么节点的左子节点是 2*index+1，节点的右子节点是 2*index+2，它的父节点是 （index-1）/2。

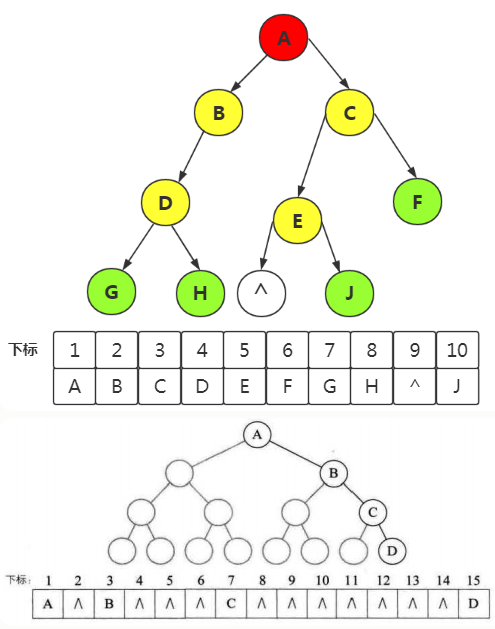
4、二叉树的顺序存储结构

一般树很难用数组存储，但完全二叉树可以，（从上->下，从左->右，层序遍历）。同时可以利用完全二叉树的性质5，快速获得结点的双亲与孩子位置。

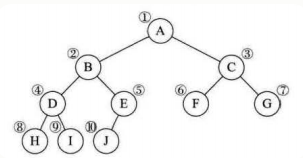
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，可以使用性质五来提现结点之间关系。这就是完全二叉树的优越性。

补充：对于一般二叉树也可以使用顺序存储（不过需要对空结点进行补全为^，变为一棵完全二叉树先）

我们需要结合数的结构来考虑，一棵普通的二叉树能否使用该方法。
如果是接近完全二叉树的二叉树，我们可以补全，
但是对于一棵类似于右斜二叉树，则完全没有必要，会大量浪费空间

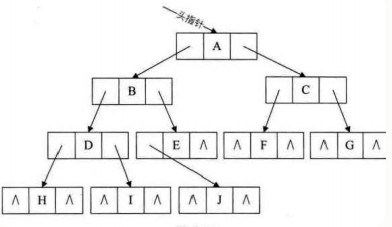
5、二叉链表

//二叉树的二叉链表结点结构定义
typedef struct BiTNode    //结点结构
{
    TElemType data;    //结点数据
    struct BiTNode *lchild, *rchild;    //左右孩子指针
}BiTNode,*BiTree;

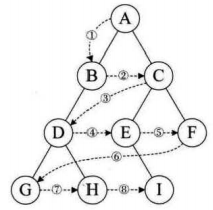
6、二叉树的遍历（递归方式）

1）前序遍历（根左右，从根节点开始遍历）

void PreOrderTraversal(BinTree BT)
{
    if (BT)
    {
        printf("%d", BT->data);
        PreOrderTraversal(BT->lchild);
        PreOrderTraversal(BT->rchild);
    }

}

2）中序遍历（左根右，注意从最左侧叶子节点开始遍历）

void InOrderTraversal(BinTree BT)
{
    if (BT)
    {
        InOrderTraversal(BT->lchild);
        printf("%d", BT->data);
        InOrderTraversal(BT->rchild);
    }
}

3）后序遍历（左右根，依然从最左侧叶子节点开始）

void PostOrderTraversal(BinTree BT)
{
    if (BT)
    {
        PostOrderTraversal(BT->lchild);
        PostOrderTraversal(BT->rchild);
        printf("%d", BT->data);
    }
}

4）层序遍历（顺序存储）利用队列。

import java.util.*;
/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;
    public TreeNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        Queue<TreeNode> queue=new LinkedList<>();
        ArrayList<Integer> list=new ArrayList<Integer>();
        if(root==null)
            return list;
        queue.offer(root);
        while(!queue.isEmpty())
        {
            int size=queue.size();
            for(int i=0;i<size;i++)
            {
                TreeNode node=queue.poll();
                list.add(node.val);
                if(node.left!=null) queue.offer(node.left);
                if(node.right!=null) queue.offer(node.right);
            }
        }
        return list;
    }
}

 二叉树前、中、后三种遍历的非递归实现方式：

前序和后序遍历：前序遍历和后序遍历归为一类,所用思想基本一模一样:
前序遍历的步骤为 ：
　　①对root进行异常处理
　　②将root压入栈
　　③while循环遍历,终止条件为栈为空，所有元素均已处理完
　　④从栈顶取元素读,取并存入结果
　　⑤将取出元素的右、左节点分别压入栈内，以便下次循环取元素时为本次节点的左,右子节点.
运用辅助栈,保存遍历到的节点(用栈后入先出的特性,控制已经遍历到的节点的访问顺序). 以前序深度优先遍历为例,先访问根节点,然后访问左树,左树全部访问完了,再访问右树
后续遍历思想: 左-右-根;可以视为, 根-右-左,然后结果转置即可. 如前面示意图,根右左,访问顺序则为:ACFBED;可以看出,这样访问刚好为后续遍历的转置. 根右左访问与前序(根左右)遍历操作思想一模一样

①前序遍历

   /**
     * 前序遍历,迭代法
     */
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null) stack.push(node.right);  //先压入右节点，后出栈
            if (node.left != null) stack.push(node.left);  //后压入左节点，先出栈
        }
        return result;
    }

②后序遍历

public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if(root == null) return result;
        Deque<TreeNode> stack=new ArrayDeque<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node=stack.pop();
            result.add(node.val);  //结点添加顺序为  根右左
            if(node.left!=null) stack.push(node.left);
            if(node.right!=null) stack.push(node.right);
        }
        Collections.reverse(result);  //反转为：左右根
        return result;
    }

③中序遍历

中序遍历思路: 中序遍历迭代法思路不同于前序和后序.
　　①首先针对对当前节点,一直对其左子树迭代并将非空节点入栈
　　②节点指针迭代为空(到树底了)后不再入栈,然后取栈顶元素,存结果;
　　③将当前指针用出栈的节点的右子节点替代,然后回到第一步继续迭代,直到当前节点为空且栈为空.

public List<Integer> inorderTraversal(TreeNode root){
        List<Integer> result = new ArrayList<>();
        if(root==null) return result;
        Deque<TreeNode> stack = new ArrayDeque<>();
        while (root!=null||!stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root=root.left;
            }
            TreeNode node=stack.pop();
            result.add(node.val);
            root=node.right;
        }
        return result;
    }

参考