0-1knapsack

Python 实现0-1背包问题（回溯法）

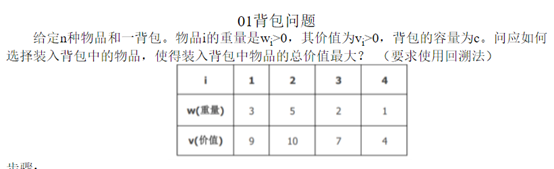
题目

解题思路

回溯法：为了避免生成那些不可能产生最佳解的问题状态，要不断地利用限界函数(bounding function)来处死那些实际上不可能产生所需解的活结点，以减少问题的计算量。这种具有限界函数的深度优先生成法称为回溯法。

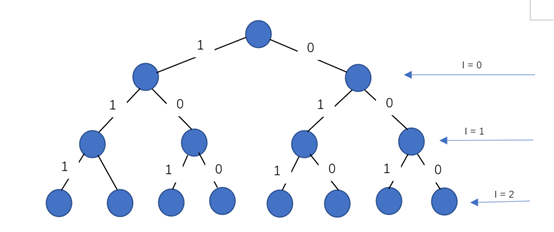
1. 确定问题的解题空间树：从n个集合中求取最优解，很显然其解空间是子集树（每个物品要么装入，要么不装入）。每个结点表示背包的一种选择状态。

2. 确定问题的扩展规则：i 表示层数即对第i个节点进行处决，n表示物品个数，问题从0层开始进行物品的选择，op表示解向量，x代表问题操作中所做的决策（0：不选；1：选择）所以有两种情况：

   • i>=n ：x操作向量的结果拷贝给op向量，max_v得到赋值（如果max_v小于了cv）

   • i<n：

     ①x[i]=1:当前重量追溯累加直到超出c背包容量，如若访问到了最后一个i节点，再进行退回操作（即cw-=w[i],cv-=v[i]）

     ②x[i]=0:直接跳向下一节点进行决策如此递归

思维导图

代码部分

max_v = 0# 最大价值
cw = 0# 当前重量
cv = 0# 当前价值
op = 0# 解向量
def backtrack(i):
    global max_v,cv,cw,op
    if i >=n:
        if max_v < cv:
            max_v = cv
            op = x[:]
    else:
        if cw+w_v[i][0]<= c:
            x[i] = 1
            cw+=w_v[i][0]
            cv+=w_v[i][1]
            backtrack(i+1)
            cw-=w_v[i][0]
            cv-=w_v[i][1]
        x[i] = 0
        backtrack(i+1)
if __name__ == '__main__':
    n,c = map(int,input().split())
    w_v = list()
    x = [0 for i in range(n)]# 定义过程操作列表
    j =0
    for i in range(n):
        w_v.append(tuple(map(int,input().split())))
    backtrack(0)
    print("the max value is :",max_v)
    for i in op:
        j += 1
        if i==1:
            print("put the {0}st into pack".format(j))

结果展示

4 10

3 9

5 10

2 7

1 4

the max value is : 26

put the 1st into pack

put the 2st into pack

put the 3st into pack