Convolutional Neural Networks for Visual Recognition 8

Convolutional Neural Networks (CNNs / ConvNets)

前面做了如此漫长的铺垫，现在终于来到了课程的重点。Convolutional Neural Networks， 简称CNN，与之前介绍的一般的神经网络类似，CNN同样是由可以学习的权值与偏移量构成，每一个神经元接收一些输入，做点积运算加上偏移量，然后选择性的通过一些非线性函数，整个网络最终还是表示成一个可导的loss function，网络的起始端是输入图像，网络的终端是每一类的预测值，通过一个full connected层，最后这些预测值会表示成SVM或者Softmax的loss function，在一般神经网络里用到的技巧在CNN中都同样适用。

那么，CNN与普通的神经网络相比，又有哪些变化呢？CNN的网络结构可以直接处理图像，换句话说CNN的输入就是直接假设为图像，这一点有助于我们设计出具备某些特性的网络结构，同时前向传递函数可以更加高效地实现，并且将网络的参数大大减少。

Architecture Overview

前面介绍的普通的神经网络，我们知道该网络接收一个输入，通过一系列的隐含层进行变换，每个隐含层都是由一些神经元组成，每一个神经元都会和前一层的所有神经元连接，这种连接方式称为 full connected，每一层的神经元的激励函数都是相互独立，没有任何共享。最后一个full connected层称为输出层，在分类问题中，它表示每一类的score。

一般来说，普通的神经网络不能很好地扩展到处理图像，特别是高维图像，因为神经元的连接是full connected的方式，导致一般的神经网络处理大图像的时候将会引入海量的参数，而这样很容易造成overfitting。

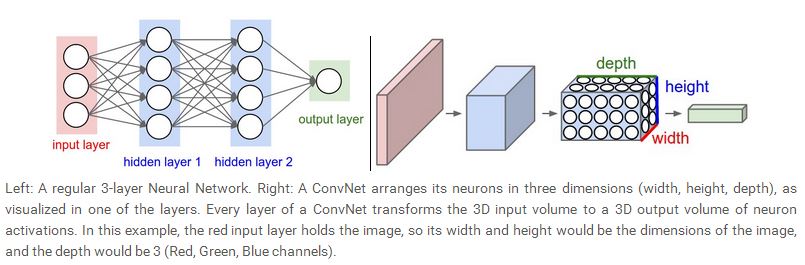
而CNN，利用了输入是图像这一事实，他们用一种更加明智的方法来设计网络结构，具体说来，不像普通的神经网络，CNN中的每一层的神经元被排列成一个三维模型：拥有width，height以及depth。这里的depth指的是CNN每一层的纵深，并非指整个CNN结构的纵深。比如，对于CIFAR-10数据库来说，输入是一个三维的volume，32×32×3，分别对应width，height和depth，我们将会看到，CNN中，每一层的神经元只跟前一层的部分神经元相连，而没有full connected，而且最后的输出层是一个1×1×10的volume，因为最后一层表示每一类的score，CNN通过这种结构，将一个输入的图像最后转化成一个表示每一类score的向量，下图给出了两种神经网络的示意图：

上图左边是一般的神经网络，这个网络有两个隐含层，右边是CNN，将每一层的神经元排列成一个三维的volume，可以将3D的输入volume转化为3D的输出volume.

Layers used to build ConvNets

上一节已经提到，CNN的每一层都将某种输入通过某些可导函数转化为另一种输出，一般来说，我们主要利用三种类型的layer去构建一个CNN，这三种类型的layer分别是convolutional layer, pooling layer 以及full connected layer，这三种类型的layer通过组合叠加从而组成一个完整的CNN网络。我们先来看一个简单的例子，以CIFAR-10数据库为例，我们要设计一个CNN网络对CIFRA-10进行分类，那么一个可能的简单结构是：[INPUT-CONV-RELU-POOL-FC]，其中：

INPUT：[32×32×3] 表示输入层，是图像的像素值，这种情况下表示图像是宽为32个像素，高为32个像素，并且有R,G,B三个通道。

CONV： 是卷积层，计算输入层的局部神经元与连接到CONV层神经元的连接系数的点积，如果假设depth是12的话，那么可能的输出就是[32×32×12]。

POOL： 这一层主要执行降采样的功能，可能的输出为[16×16×12]。

FC： 这一层计算最终的每一类的score，输出为[1×1×10]。与普通的神经网络一样，这一层的神经元与上一层的所有神经元都会连接。

所以，利用这种结构，CNN通过一层一层的传递作用，将原始的图像最后映射到每一类的score。我们可以看到，有些层有参数，有些层没有参数。特别地，CONV/FC层不仅仅只是通过激励函数做转化，而且参数（权值，偏移量）也起到非常重要的作用，另一方面，POOL/RELU 层只是固定的函数在起作用，并没有涉及到参数，CONV/FC层的参数将通过梯度下降的方法训练得到，使得训练样本的预测值与目标值吻合。

下图给出了一个典型的CNN结构。

总之，CNN可以总结如下：

1)：一个CNN结构是由一系列的执行不同转化功能的layers组成的，将输入的原始图像映射到最后的score。

2)：整个网络结构，只有少数几类不同功能的layer (CONV/FC/RELU/POOL 是目前比较流行的几种)。

3)：每一层都接收一个3-D的数据体，最后也会输出一个3-D的数据体。

4)：有些层有参数(CONV/FC)，有些层没有(RELU/POOL)。

5)：有些层还可能有hyperparameters(CONV/POOL/FC)，有些层则没有(RELU)。

接下来，我们要描述每一类layer的作用，以及相关的参数。

Convolutional Layer

Conv layer是CNN网络的核心部件，它的输出可以看成是一个3-D的数据体，CONV 层包含一系列可学的filters，这些filter的尺寸都很小，但是可以扩展到input的整个depth，前向传递的时候，filter在输入图像上滑动，产生一个2-D的关于filter的激励映射，filter只会和局部的一些像素（神经元）做点积，所以每一个输出的神经元可以看成是对输入层的局部神经元的激励，我们希望这些filter通过训练，可以提取某些有用的局部信息。我们接下来探讨到更加详细的细节。

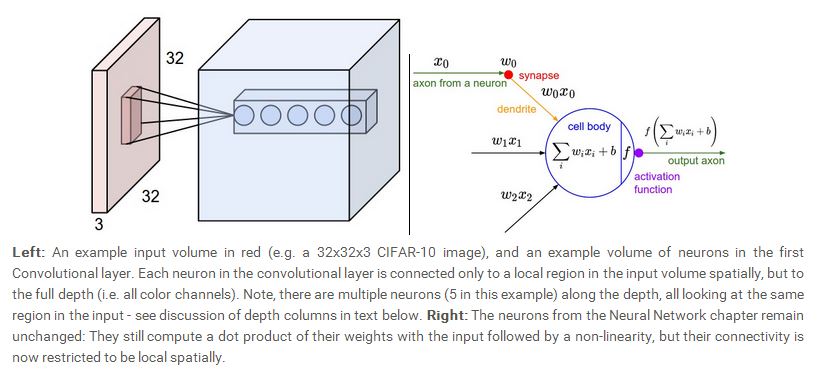
当输入是高维的变量，比如图像等，如果采用full connected的连接是不切实际的，相反，我们会采用局部连接的方式，那么每一个局部区域我们称为receptive field，这种局部连接是针对输入层的宽，高这两个维度来说，但是对于第三个维度depth来说，依然是要完全连接，所以我们处理局部空间在宽，高维度与depth这个维度是不一样的。宽，高维度上，我们采取局部连接，但是对于depth维度，我们采用全连方式。

比如，如果一个输入图像的尺寸是[32×32×3]，我们定义下一层神经元的receptive field的尺寸是5×5，那么考虑到depth这个维度，最终每一次都有5×5×3=75个神经元与CONV层的一个神经元连接，意味着有5×5×3=75个权值。

再比如，假设现在有一个输入的数据体是16×16×20，那么如果定义一个receptive field为3×3的连接方法，那么在CONV层的每一个神经元最终连接到上一层神经元的个数是3×3×20=180。

这两个例子都说明了，在宽，高维度我们采用局部连接的方式，而在depth维度，我们会全部连接。下面给出了一个简单的示意图：

前面我们介绍了CONV层的神经元与前一层的连接方式，但是CONV层本身的神经元如何排列，而且其尺寸如何，我们还没有讨论，事实上，CONV层本身的神经元如何排列以及CONV层的尺寸由三个因素决定：depth，stride，zero padding。

首先，depth决定了CONV层中有多少神经元可以与前一层相同的神经元相连，这个类似普通的神经网络，在普通的神经网络中，我们知道每一个神经元都与上一层的所有神经元相连，所有每一层的所有神经元都是与上一层相同的神经元相连。我们将会看到，所有这些神经元将通过学习从而对输入的不同特征产生应激作用，比如，如果第一个CONV层接收的是原始输入图像，那么沿着depth维度排列的神经元（注意：这些神经元连接的输入层的神经元都相同）可能对不同的特性（比如边界，颜色，斑块）等产生激励。我们将这些连接到输入层同一区域的神经元称为一个depth volume。

接下来，我们必须指定stride，这个决定了我们如何在CONV层排列depth volume，如果我们指定stride为1，那么depth volume的排列将会非常紧凑，意味着隔一个神经元就会有一个depth volume，这样会产生比较大的重叠，而且输出的尺寸也会很大，如果我们增大stride，可以减少重叠，并且可以减少输出的尺寸。

zero padding就是为了控制输出的尺寸，对输入图像的边缘进行补零操作，因为卷积可能使输出图像的尺寸减少，有的时候为了得到与输入一样的尺寸，我们可以在做卷积之前先对输入图像的边缘补零，即先增大输入图像的尺寸，这样可以使得最终的卷积结果与补零前的输入图像的尺寸一致。

我们可以看到，输出层有一个depth，一个spatial size，depth可以指定，spatial size与输入层的size(W)，receptive field的size，即filter的size(F)，我们定义的stride(S)，还有边缘的zero padding的size(P)有关，可以看成是这些变量的一个函数，我们可以证明最终输出的spatial size为：(W−F+2P)/S+1。

我们可以看一个例子，如果输入图像的尺寸为[227×227×3]，我们设计一个CONV层，每个神经元的receptive field为11，即F=11，stride为S=4，没有zero padding，那么输出的CONV层的spatial size为(227−11)/4+1=55，如果我们定义CONV层的depth为96，那么这个CONV层的最终尺寸为55×55×96, 从上面这个定义看出，这55×55×96个神经元中的每一个都和输入图像的一个11×11×3的局部区域相连，并且每一个depth volume中含有96个神经元，这96个神经元与输入图像的同一个11×11×3的局部区域相连，它们唯一的区别在于连接权值的不同。

继续看上面的例子，我们知道CONV层有55×55×96=29040个神经元，每个神经元都与输入层的11×11×3个神经元连接，那么CONV层的每一个神经元都将有11×11×3=363个权值外加一个bias，那么最终的系数将会达到29040×(363+1)=105,705,600。很明显，这个系数量太大了。

我们可以利用一个合理的假设来大大系数的数量，我们将CONV层看成一个depth volume，比如上面这个例子，CONV层是一个55×55×96的volume，其depth为96，那么每一个55×55的排列可以看成是一个slice，那么这个CONV层有96个slices，每一个slice的尺寸都为55×55，我们让每一个slice里的神经元都共享一组同样的连接系数，或者说同样的filter，那么意味着每一个slice都只有11×11×3个不同的系数，整个CONV层将只有11×11×3×96=34848，如果每个slice的神经元也共享同样的bias，那么最终的系数为34848+96=34944个，我们看到，通过这种假设，系数的总量大大减少了，每一个slice里的55×55个神经元都共享同样的连接系数，实际运算中，所有的神经元都会计算相应的梯度，但是这些梯度最终会相加，在每一个slice中只做一次更新。

如果每一个slice里的神经元都共享同样的连接系数，那么实际运算的时候可以利用卷积运算，其实这也是这个网络名称的由来，卷积在其中发挥重要的作用，所有我们有的时候把这些系数称为filter或者kernel，卷积的结果就是activation map，每一个activation map叠加，最后形成一个55×55×96的volume。

总结一下CONV的特点：

接收一个尺寸为W1×H1×D1的volume。

定义一些相关的hyperparameter，比如filter的个数K，filter的size或者称为receptive fieldF，stride S以及zero padding P，通过运算可以得到一个如下的

尺寸为：W2×H2×D2的depth volume，其中，W2=(W1−F+2P)/S+1，H2=(H1−F+2P)/S+1，D2=K，通过参数共享，每个slice

会有一个F⋅F⋅D1的kernel，一共有K个kernel，所以一共有系数(F⋅F⋅D1)⋅K，在输出的数据体中，每一个slice的尺寸都是W2×H2，一共有D2=K个slice。

CONV层的backpropagation 同样是卷积运算，这个具体的细节留到后面详细探讨。

Pooling Layer

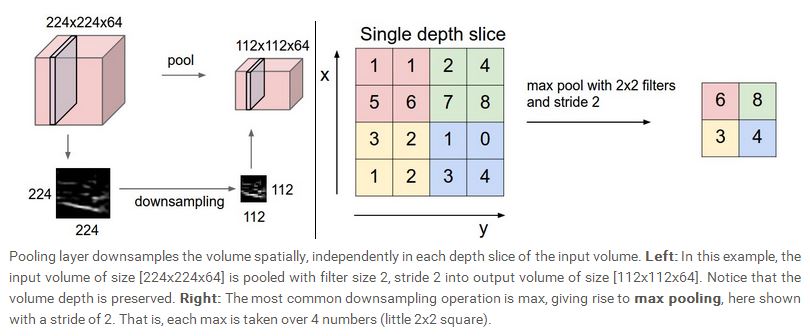
一般来说，在两个CONV layer之间，会插入一共pooling layer，pooling layer的作用一个是减少输入的空间尺寸，从而可以降低参数的数量及运算量，同时也可以控制overfitting。Pooling layer与上一层的每一个slice是一一对应的，没有相互交叉。最常见的pooling 运算是采用max 操作，在2×2的一个空间区域内，以stride为2进行将采样，pooling操作只在宽，高维度上进行，所以不会改变depth，输出与输入的depth将会一样。总结来说，Pooling layer：

接收一个尺寸为W1×H1×D1的volume。定义一些相关的hyperparameter，filter的size或者称为receptive fieldF，stride S，通过运算可以得到一个如下的尺寸为：W2×H2×D2的depth volume，其中，W2=(W1−F)/S+1，H2=(H1−F)/S+1，D2=D1，pooling layer不会又系数，也不会使用zero padding。下图给了一个pooling的示意图：

max pooling 的backpropagation，简单来说就是只对输入的最大值进行梯度运算，所以每次前向运算的时候，最好可以将最大值的位置记录下来，这样每次backward的时候就可以方便运算。

Full-connected Layer

FC layer就像普通神经网络里的隐含层一样，FC layer中的每一个神经元与上一层所有的神经元都会连接(full connected)，涉及到的运算也和普通的神经网络一样。值得注意的一点是，FC与CONV layer之间的区别仅在于CONV layer里的神经元只和上一层的局部神经元相连，但是两者的运算模式是一样的，都是做点积，因此在FC与CONV之间存在相互转换的可能。

对于CONV layer，如果我们从FC的角度来看，相当于乘了一个非常大的稀疏矩阵(大部分系数为0，因为只有局部神经元的连接是有效的)，而且这些非0系数在某些block中是相等的(系数共享)。反过来，任何FC layer也可以有效地转换成CONV layer，比如一个神经元个数K=4096的FC layer，接收的输入是7×7×512，我们可以等同于利用一个CONV层其hyperparameter设定为 F=7, P=0, S=1, K=4096，我们设定filter的spatial size与输入的spatial size是一样的，这样最后会得到一个1×1×4096的输出。

上面所说的两种转换，其中FC 转换为CONV 在实际运算中非常有用，考虑一个实际的CNN网络，最原始的输入为224×224×3的图像，经过一系列的转换运算，我们得到了一个尺寸为7×7×512的volume，接下来我们用两个FC layer，将这个volume转换为尺寸为4096的volume，最后连接到size为1000的输出，我们可以将这三个FC layer用CONV layer的运算模式来表示。

将第一个FC layer替换成CONV layer，其filter size 为7，我们可以得到1×1×4096的输出。将第二个FC layer替换成CONV layer，其filter size 为1，输出的volume为1×1×4096。同样，最后一个FC layer用filter size为1的CONV layer替换，最后的输出为1×1×1000。

上面所说的每一个转换都涉及到系数矩阵的reshape问题，这种转换可以让我们将CNN结构非常有效的在更大的图像上滑动。比如，如果一个224×224的图像生成了一个尺寸为7×7×512的volume，从224降到7，一共降了32倍，那么，如果输入的图像是384×384，那么我们会生成一个12×12×512的volume，那么我们利用这三层FC layer，转换成CONV layer，我们最终会得到6×6×1000的输出，意味着每一类的score不只是一个数，而是一个6×6的数组。

我们可以看到，如果图像保持不动，而CNN网络每次以32个像素的stride在图像上移动，最后得到的结果是一样的。

一般来说，利用CNN网络做一次遍历，得到一个6×6的score，比重复调用CNN结构36次计算其在图像不同位置之间的score要更加高效，因为这36次调用使用的是同一个网络结构，共享完全一样的系数及运算模式。这种实际应用中，是一种提高分类性能的技巧，比如我们将一幅图先放大，然后再利用CNN结构做遍历，最后将所有得到的score求平均。

最后一点，如果我们想将CNN网络以小于32的stride有效地应用在图像上，可以通过多次前向传递运算达到目的。比如，我们想以16个像素的stride遍历图像，可以做两次运算，第一次是直接将CNN网络在原图上做遍历，第二次，先将原图在宽，高方向分别平移16个像素，然后在平移后的图像上做遍历。

ConvNet Architectures

我们已经看到，CNN网络一般只有几种类型的layer：CONV，POOL(一般默认为max pooling)以及FC，一般我们也会把RELU单独列为一层，用来执行非线性运算的操作，我们看看这些layer如何构建一个完整的CNN网络。

比较常见的模式是先叠加几层CONV-RELU layer，后面连上POOL layer，这样将输入的图像逐渐减少到一个比较小的尺寸，接来下，就连上Full connected layer，最后的FC layer是输出，所以一般比较常见的模式如下所示：

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

其中*表示重复叠加的意思，而POOL?表示这是可选择的，而且N>=0，一般N<=3，M>=0，K>=0，通常K<=3，下面是一些常见的CNN网络结构。

INPUT -> FC，这是最普通的线性分类器，N = M = K = 0.

INPUT -> CONV -> RELU -> FC

INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC 我们看到CONV layer后面连着Pool layer。

INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC 我们看到在连接POOL layer之前，已经有两个CONV layer叠加到一起了。

一般我们会选择小尺寸的filter，这在实际应用中的效果会更好。一般来说，输入图像的尺寸最好是2的幂次方，比如32,64,96,224,384以及512。CONV 层一般用比较小的filter，比如3×3或者5×5，stride一般设为1，为了让卷积运算之后图像的尺寸保持不变，有的时候会引入zero padding，zero padding的大小一般为P=(F-1)/2，pool layer执行降采样的功能，最常见的pool是用max pooling，在一个2×2的区域内，这样相当于将图像缩小一半，在设计CNN网络的时候，对于这些参数要小心设定，要确保每个layer的输出尺寸与设想的一致。

现在流行的CNN网络结构都是非常庞大的，比较著名的CNN结构有如下几个LeNet, AlexNet, ZF Net, Google Net, VGGNet,具体的介绍可以参考课程网站。这里不再详述。

声明：lecture notes里的图片都来源于该课程的网站，只能用于学习，请勿作其它用途，如需转载，请说明该课程为引用来源。

http://cs231n.stanford.edu/