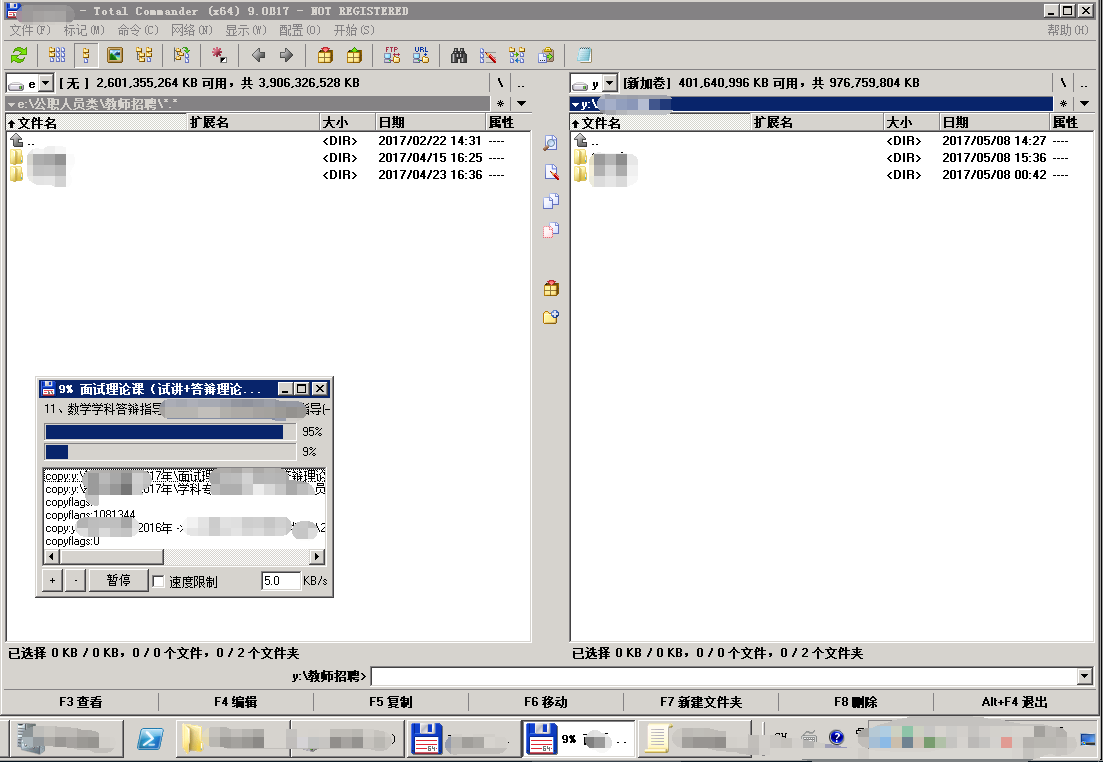
使用Total Commander Portable，可以批量拷贝多个位于相同或不同目录的文件（夹）到指定的相同或不同的目录。这样避免了同时复制多个大的文件造成的速度减慢；将所有任务手动操作之后，剩下的传输任务交给它即可，不必有人值守。

　　拖动后，请在弹出的对话框中选择“队列”。

　　该软件下载地址为：http://fq.wc.lt//up/1494468385.zip

移动文件步骤：

4、点击“F2队列”（若点击确定，速度可能会慢）。

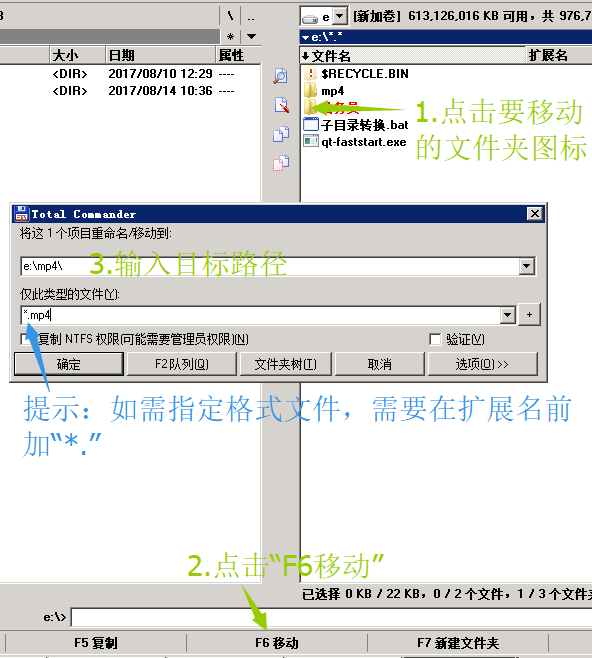
复制文件：

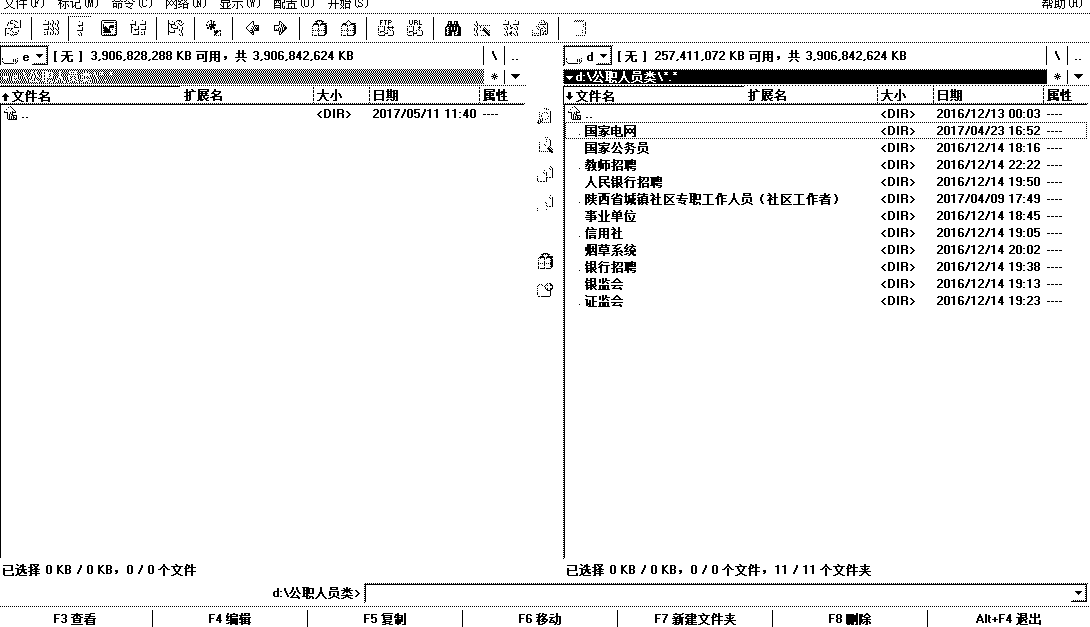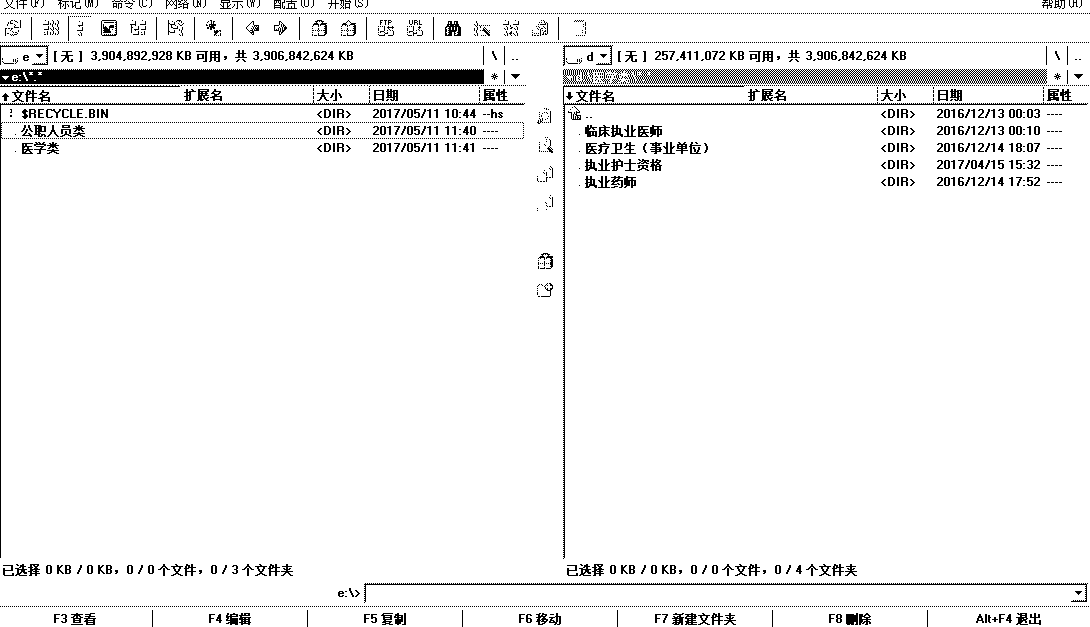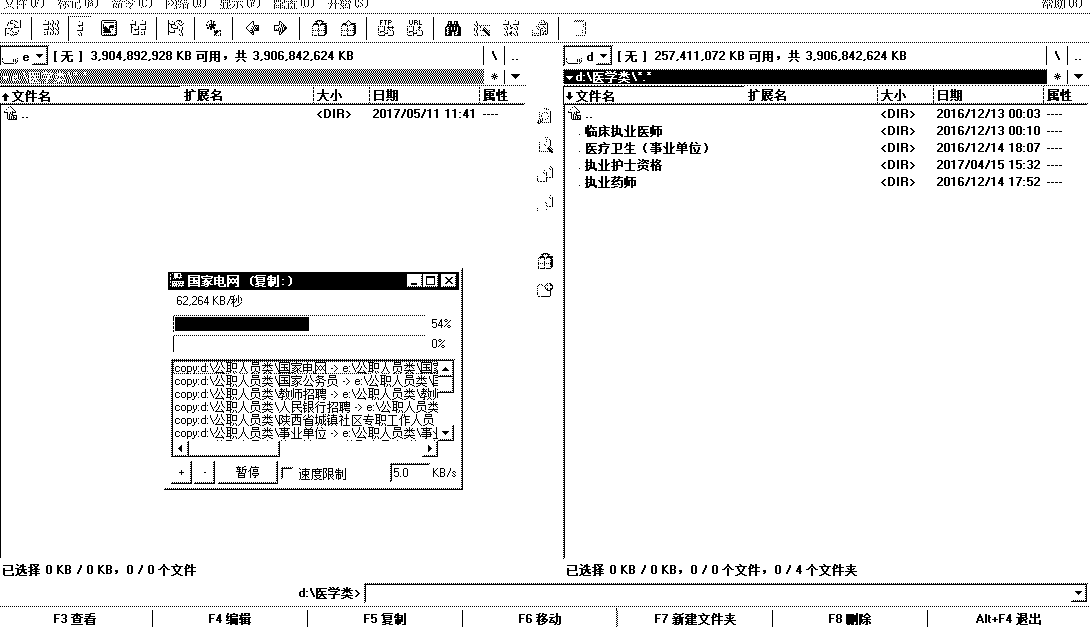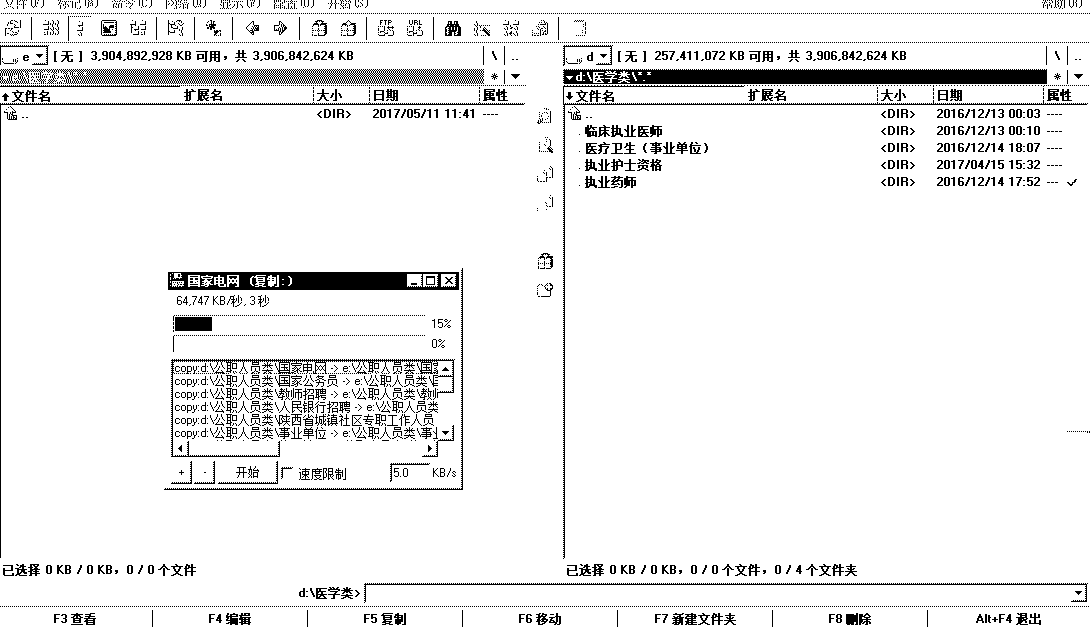
复制空文件夹

  1. 运行cmd；
  2. 输入：xcopy d:\data d:\data2 /T /E（前者代表原文件夹，后者代表输出文件夹）

摘自：https://wenku.baidu.com/view/038c8006bed5b9f3f90f1c99.html

【文件拷贝】使用Total Commander Portable拖动拷贝文件，支持队列的更多相关文章

  1. total commander相关设置

    一. 中文语言包 在官方网站上提供有简体中文语言包,下面的说明以此为准.下载的语言包放至Total Commander安装目录下的Language子目录中.从菜单“Configuration”→“Op ...

  2. 如何修改Total Commander配件文件的位置

    今天测试了一下Total Commander最新版的安装文件,测试完成后,并删除.结果导致原先一直在使用的绿色版的Total Comander配件文件变成了测试的配件文件,导致许多配置都丢失了,因此不 ...

  3. C# 文件操作（全部） 追加、拷贝、删除、移动文件、创建目录 修改文件名、文件夹名

    原文:C# 文件操作(全部) 追加.拷贝.删除.移动文件.创建目录 修改文件名.文件夹名 本文也收集了目前最为常用的C#经典操作文件的方法,具体内容如下:C#追加.拷贝.删除.移动文件.创建目录.递归 ...

  4. JAVA IO流编程 实现文件的写入、写出以及拷贝

    一.流的概念 流:数据在数据源(文件)和程序(内存)之间经历的路径. 输入流:数据从数据源(文件)到程序(内存)的路径. 输出流:数据从程序(内存)到数据源(文件)的路径. 以内存为参照,如果数据向内 ...

  5. Python 文件复制&按目录树结构拷贝&批量删除目录及其子目录下的文件

    文件复制&按目录树结构拷贝&批量删除目录及其子目录下的文件 by:授客 QQ:1033553122 测试环境: Python版本:Python 3.3.2 Win7 64 代码实践 # ...

  6. 在Myeclipse中拷贝一个web项目，但是tomcat文件夹中没有更新，需要进行修改才能更新。

    1.在Myeclipse中拷贝一个web项目,但是tocat文件夹中没有更新,需要进行修改才能更新. 2.方法:右键这个工程,然后Properties->MyEclipse->Projec ...

  7. Docker拷贝宿主机与容器中的文件

    如果我们需要将宿主机文件拷贝到容器内可以使用 docker cp 命令,也可以将文件从容器内拷贝到宿主机 将宿主机文件拷贝到容器内 docker cp 要拷贝的宿主机文件或目录 容器名称:容器文件或目 ...

  8. Linux_拷贝，剪切，删除和创建文件

    cp 你要拷贝的文件 + 目录/带路径的文件名(在拷贝的同时,让这个文件重新命名) cp /tep/dir01  ~  代表将dir01拷贝到当前用户的家目录中 cp /tep/dir02  ~/di ...

  9. Total Commander 常用快捷键（并附快捷键大全）

    Total Commander 常用快捷键 喜欢用Total Commander的人,都会记住它的一些快捷键,这会给你的操作带来很大的方便,以下是经常会用到的快捷键,大家可以记住一些自己用得最多的操作 ...

随机推荐

  1. 【关于安装mysql5.6的一些问题总结】

    1:安装msyql5.6介质(mysql-5.6.24-winx64.msi)以后没有myslq服务: 解决: 管理员身份cmd进入bin目录: mysqld.exe -install Service ...

  2. 安装MySQL出现1045错误,卸载不干净

    安装MySQL出现1045错误 一.运行环境 MySQL mysql-5.1.26-rc-win32 操作系统:Windows 7 X64 二.问题描述 安装MySQL过程中会涉及对root密码的设置 ...

  3. sqlserver2012——SqlCommand创建对象的三种方法

    1.使用不带参构造函数 SqlCommand cmd = new SqlCommand(); cmd.Connection = SqlConnnection对象: cmd.CommandText=Sq ...

  4. python 里 np.array 的shape (2,)与(2,1)的分别是什么意思，区别是什么？

    numpy.ndarray.shap是返回一个数组维度的元组. (2,)与(2,1)的区别如下:   ndarray.shape:数组的维度.为一个表示数组在每个维度上大小的整数元组.例如二维数组中, ...

  5. 【leetcode 968. 1028. 从先序遍历还原二叉树】解题报告[待完善...]

    思路:用一个栈来管理树的层次关系,索引代表节点的深度 方法一: TreeNode* recoverFromPreorder(string S) { /* 由题意知,最上层节点深度为0(数字前面0条横线 ...

  6. php soap连接https的wsdl报错SOAP-ERROR: Parsing WSDL:Couldn't load from

    转发:https://blog.csdn.net/keyunq/article/details/51804728 SOAP-ERROR: Parsing WSDL:Couldn’t load from ...

  7. 一切从这里起始（左耳听风 ARTS 6号小组 week 1）

    ARTS 具体要求: 1.每周至少做一个 leetcode 的算法题2.阅读并点评至少一篇英文技术文章3.学习至少一个技术技巧4.分享一篇有观点和思考的技术文章 1.Algorithm Two Sum ...

  8. Effective Java第一节

    第1条:考虑用静态工厂方法代替构造器 首先清楚什么是静态工厂方法? 静态工厂方法说白了就是在创建对象的时候,不是自己使用new关键字创建的,而是使用静态方法来对外提供自身的实例的方法. 比如: Fra ...

  9. CODEVS 3027 线段覆盖2

    首先,先看题.....(虽然比较简单 3027 线段覆盖 2    时间限制: 1 s  空间限制: 128000 KB 题目描述 Description 数轴上有n条线段,线段的两端都是整数坐标,坐 ...

  10. shell学习（14）- who

    Linux who命令用于显示系统中有哪些使用者正在上面,显示的资料包含了使用者 ID.使用的终端机.从哪边连上来的.上线时间.呆滞时间.CPU 使用量.动作等等. 使用权限:所有使用者都可使用. 语 ...