Dotfuscator 的使用方法

打开Dotfuscator工具，选择“Create New Project”

在Input选项中选择需要混淆的文件

把 Disable String Encryption 设为 NO，即启用字符串加密；检查 Disable Control flow、Dsiable Renaming 也为 NO，即保证控制流和混淆功能打开，其他默认。如下图：

Rename 选项勾选“Use Enhanced Overload Induction”（使用增强模式），注意：不要勾选下方的“ Do not suppress on serializable types”，即序列化类型的变量不加密，否则编译后可能异常； “Renaming Scheme” 选择“Unprintable”（不可打印字符，即乱码），也可以选择其他如小写字母、大写字符、数字的方式，其他保持默认如下图

String Encryption 选项 include里勾选需要字符串加密的工程文件EXE、DLL等然后点击绿色小三角生成项目，如下图

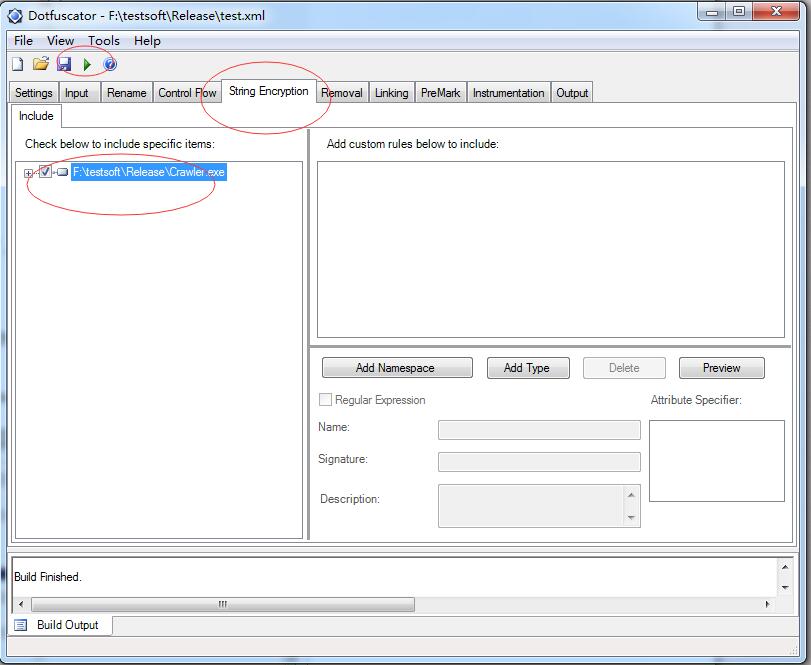
完成后使用.Net Reflector查看生成的文件，如下图

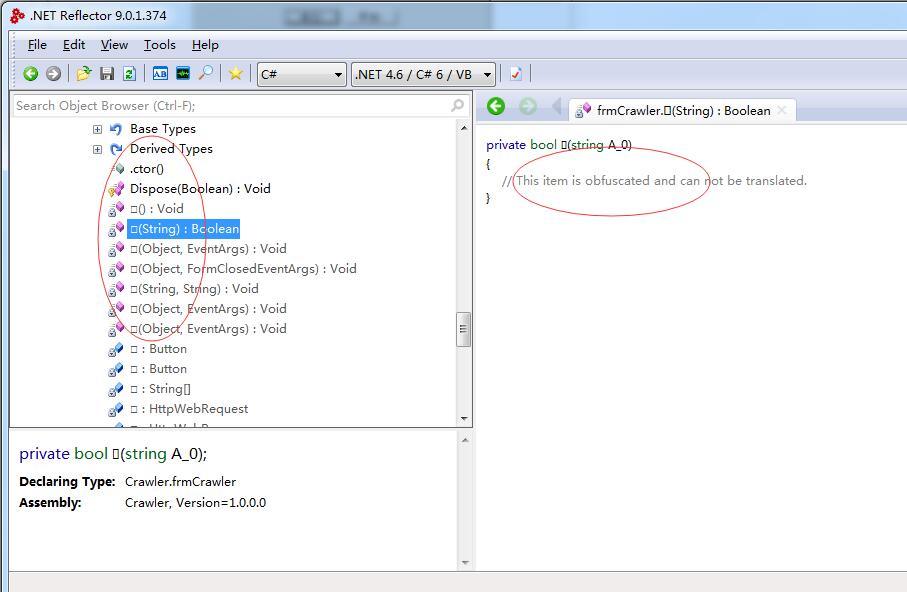
参考http://www.cnblogs.com/icyJ/p/dotfuscator.html