GC回收的对象

垃圾收集（Carbage Collection）

 　　java内存在运行时区域，程序计数器、java虚拟机栈、本地方法三个区域都是线程私有的内存区域，随着线程的启动和销毁而分配和回收。栈帧随着方法的调用和退出而执行入栈和出栈。每一个栈帧分配多少内存在编译期间就已经确定下来了，所以这几个内存区域具有确定性，不用过多考虑内存回收的的问题。会随着线程的结束或者方法的结束而回收内存。

　　java中的GC工作主要针对java 堆 和 方法区这些内存区域。

如何判断对象是否"活着"

（1）引用计数算法

    在对象中添加一个引用计数器，每在一个地方引用了该对象的时候，引用计数器+1，当引用失效的时候，引用计数器-1。

    但是在java中没有使用该算法来管理内存，因为这个算法很难解决对象互相引用的问题。

 

（2）根搜索算法

    通过一系列 "GC Roots"的对象为起点，从这些节点开始向下搜索（搜索走过的路径叫做 "引用链"），当一个对象到 "GC Roots"对象没有任何引用链相连（用图论说明就是指所有的 "GC Roots" 与对象不可达），说明这个对象是不可用的。java 和 C#使用根搜索算法。

 

GC Roots对象

• 虚拟机栈（栈帧中本地变量表）中的引用的对象
• 方法区中类静态属性引用的对象
• 方法区中常量引用的对象
• 本地方法中JNI引用的对象

确认是否回收

在通过算法找出没有"活着"的对象，并不是一次性的回收他们，需要经过两次标记。

回收方法区
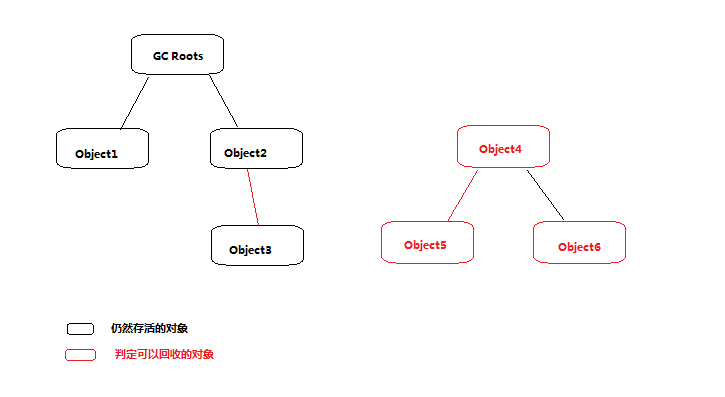
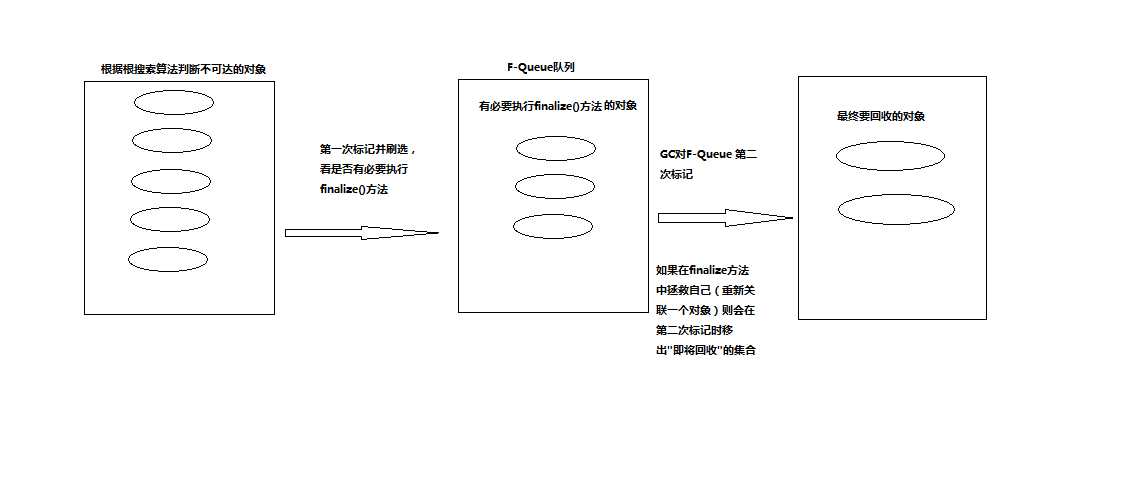
方法区主要回收的部分是废弃常量 和 无用的类。

在常量池中，有字符串abc,当没有任何的String对象的引用常量池中的 abc 常量，也没有其他地方引用这个字面量，则这个常量是废弃常量。

无用的类

1. Java堆中不存在该类的任何实例
2. 加载该类的ClassLoader被回收了
3. 该类对应的java.lang.Class 对象在任何地方没有被引用

总结

JVM如何判断 "活着" 的对象，以及对于 "死亡" 的对象判定确认回收过程。