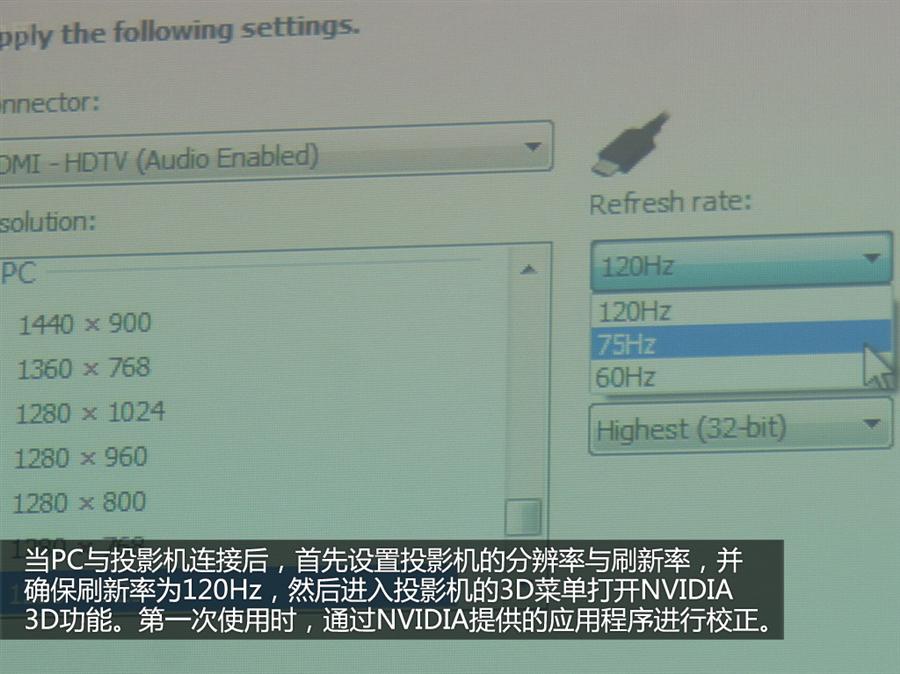
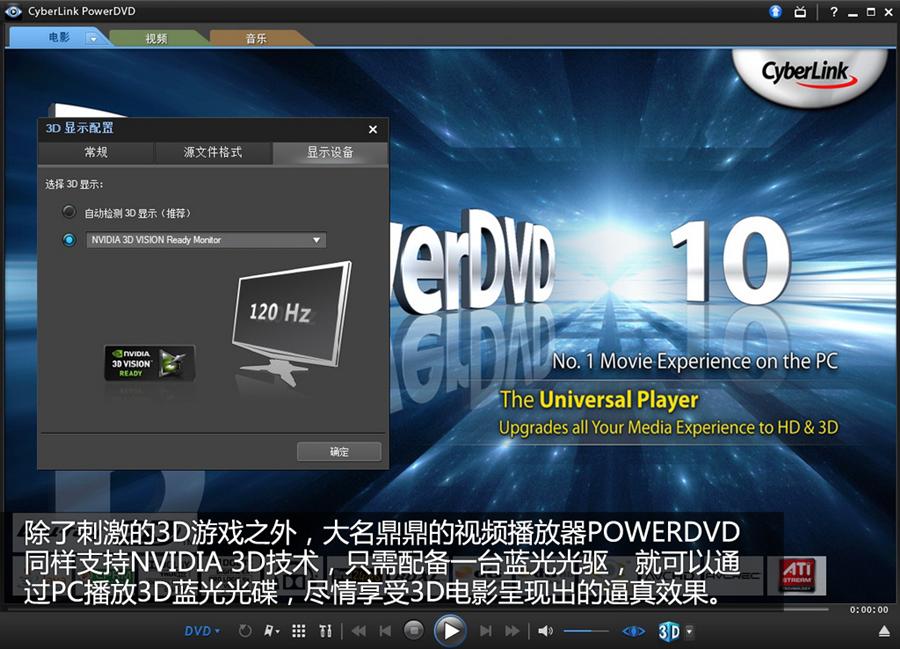
NV 3D投影方案 【转】
http://tu.pcpop.com/all-677013.htm






NV 3D投影方案 【转】的更多相关文章
- 背水一战 Windows 10 (70) - 控件(控件基类): UIElement - Transform3D(3D变换), Projection(3D投影)
[源码下载] 背水一战 Windows 10 (70) - 控件(控件基类): UIElement - Transform3D(3D变换), Projection(3D投影) 作者:webabcd 介 ...
- 3D投影
3D投影方式的几大种类: 1.快门式 主动快门式即时分式,不过我们通常用前面的叫法,快门式3D眼镜(3D Shutter Glasses,也称作LC shutter glassesor active ...
- win10 uwp 使用 Matrix3DProjection 进行 3d 投影
原文:win10 uwp 使用 Matrix3DProjection 进行 3d 投影 版权声明:博客已迁移到 http://lindexi.gitee.io 欢迎访问.如果当前博客图片看不到,请到 ...
- 在程序中使用NV 3D Vision 【转】
http://www.cnblogs.com/gongminmin/archive/2010/11/21/1883392.html 多年前NVIDIA就发布了3D Vision技术,能提供多种立体渲染 ...
- NVIDIA® Quadro® 四路缓冲 3D立体方案
http://www.nvidia.cn/object/quadro_pro_graphics_boards_cn.html NVIDIA® Quadro® 专业显卡让地球学家以及时装设计师等许多专业 ...
- DirectX 11---从空间变换来看3D场景如何转化到2D屏幕
DirectX 11---从空间变换来看3D场景如何转化到2D屏幕 在看<Introduction to 3D Game Programming with DirectX 11>的时候,发 ...
- 从0开发3D引擎(二):准备预备知识
大家好,本文介绍了开发3D引擎需要的预备知识,给出了相关的资源. 上一篇博文 从0开发3D引擎(一):开篇 了解Web 3D Web 3D的历史 目前Web 3D是基于WebGL这个Web端3D AP ...
- WPF 3D 知识点大全以及实例
引言 现在物联网概念这么火,如果监控的信息能够实时在手机的客服端中以3D形式展示给我们,那种体验大家可以发挥自己的想象. 那生活中我们还有很多地方用到这些,如上图所示的Kinect 在医疗上的应用,当 ...
- 裸眼3D立体显示技术原理详解
众所周知,现实世界是一个三维空间,除去时间这一维度,现实世界是由长度.宽度和高度三个维度组成,我们每天就生活在这个三维世界中,而现有的显示设备大多数都只能显示二维信息,并不能带给人真实的三维感觉.为了 ...
随机推荐
- python2.X中文乱码
在IDE下,加上# -- coding: UTF-8 -- 并且保证IDE也是utf-8编码. 在CMD下,这样执行会有乱码,为啥呢,因为cmd下是gbk编码的,你写的代码必须也是gbk编码的,你可以 ...
- day05_09 列表内置方法
1.0 count(计算元素出现的次数) t = ['to','be','or','not','to','be'].count('to') print(t) #>>>2 2.0 ex ...
- Leetcode 567.字符串的排列
字符串的排列 给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列. 换句话说,第一个字符串的排列之一是第二个字符串的子串. 示例1: 输入: s1 = "ab&q ...
- C++ bitset类的使用与简介
有些程序要处理二进制位的有序集,每个位可能包含的是0(关)或1(开)的值.位是用来保存一组项或条件的yes/no信息(有时也称标志)的简洁方法.标准库提供了bitset类使得处理位集合更容易一些.要使 ...
- 【bzoj3924】[Zjoi2015]幻想乡战略游戏 动态点分治
题目描述 傲娇少女幽香正在玩一个非常有趣的战略类游戏,本来这个游戏的地图其实还不算太大,幽香还能管得过来,但是不知道为什么现在的网游厂商把游戏的地图越做越大,以至于幽香一眼根本看不过来,更别说和别人打 ...
- 【POJ2774】Long Long Message (SA)
最长公共子串...两个字符串连在一起,中间放一个特殊字符隔开.求出height之后,枚举height,看两个后缀是不是分布于两段字符串..如果是,这个值就可以作为答案.取最大值即可. ; var c, ...
- c#byte数组和string类型转换
http://blog.csdn.net/rowanhaoa/article/details/42144313/ 用system.text中的encoding这个类
- iOS-读取txt文件中文乱码
一.情景描述: 后台给一个txt文件,编码是utf-8,在Mac电脑Xcode开发环境下读取txt文件内容,汉字会出现乱码,英文没有乱码这种情况. 二.尝试解决方法: 修改编码格式,尝试了NSUTF1 ...
- ai相关
学习资源 1.1 1.2 2.1 2.2 2.3 前置 octave sklearn python3 git 学习相关 link 定义 Field of study that gives comput ...
- Cookies设置,获取,删除
之前的博客,整理了下Session的存储方式和原理http://www.cnblogs.com/chinaagan/p/3200456.html. 本篇再次整理下Cookies的使用和原理. 参考博客 ...
