Luogu P3941 入阵曲【前缀和】By cellur925

题目传送门

题目大意：给你一个\(n\)*\(m\)的矩阵，每个位置都有一个数，求有多少不同的子矩阵使得矩阵内所有数的和是\(k\)的倍数。

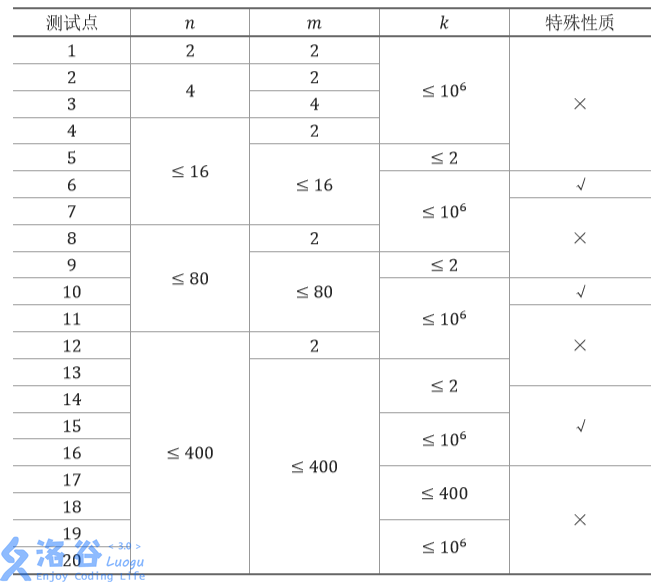
数据范围给的非常友好233，期望得到的暴力分：75分。前12个点可以用\(O(n^4)\)算法水过，对于\(<=400\)的有特殊性质2的数据，我们还可以尝试苟一下，开始用了一个什么鬼方法（？），其实我们只要枚举所有可能的矩形面积判断一下是否满足条件再加上这种矩形面积的所有可能数就行啦。

#include<cstdio>
#include<algorithm>

using namespace std;
typedef long long ll;

int n,m,k;
ll ans,mapp[450][450];

ll gcd(ll a,ll b)
{
	return b ? gcd(b,a % b) : a ;
}

void calc(ll a,ll lima,ll b,ll limb)
{
	ll cnt1=lima-a+1;
	ll cnt2=limb-b+1;
	ans+=cnt1*cnt2;
}

int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%lld",&mapp[i][j]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			mapp[i][j]+=mapp[i-1][j]+mapp[i][j-1]-mapp[i-1][j-1];
	if(n<=80||m<=2)
	{
		for(int i=1;i<=n;i++)
			for(int j=1;j<=m;j++)
				for(int l=1;l<=n&&i-l+1>=1;l++)
					for(int r=1;r<=m&&j-r+1>=1;r++)
					{
						int ii=i-l+1,jj=j-r+1;
						ll sum=mapp[i][j]+mapp[ii-1][jj-1]-mapp[ii-1][j]-mapp[i][jj-1];
						if(sum%k==0) ans++;
					}
		printf("%lld\n",ans);
		return 0;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if((i*j*mapp[1][1])%k==0) calc(i,n,j,m);
	printf("%lld\n",ans);
	return 0;
}

其实做这道题的时候感觉和昨天考试T1比较像的，我们可以很容易的想出\(O(n^4)\)算法，再根据一些性质（如单调性）优化到\(O(n^3)\)。本题要求的复杂度同样是\(O(n^3)\)。

由“\(k\)的倍数”我们可以想到另一道题：ZR某次普及膜底赛当时chengni dalao给我讲了子共七的思想，虽说后来讲了子共七那道原题，还是没A==。

我们考虑在一维序列上的情况，若\(sum[i]\)模\(k\)等于\(A\)，之后出现了一个\(sum[j]\)模\(k\)也等于\(A\)，那么显然有\([i+1,j]\)这部分的和是\(k\)的倍数（模\(k\)为\(0\)）。

我们可以推广到矩阵上的情况，像昨天一样枚举矩阵的上下界，再枚举一个左右边界，统计余数个数，这样能把复杂度压到\(O(n^3)\)。每次的计数数组要清空，但是用\(memset\)会超时，不妨用数组记录一下空间换时间。

#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;
typedef long long ll;

int n,m,moder;
ll ans,f[1000][1000],tong[1000090],b[1000090];

int main()
{
	scanf("%d%d%d",&n,&m,&moder);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%lld",&f[i][j]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			(f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+moder)%=moder;
	for(int i=0;i<n;i++)//注意是从0开始枚举
		for(int j=i+1;j<=n;j++)
		{
			tong[0]=1;
			for(int k=1;k<=m;k++)
			{
				b[k]=(f[j][k]-f[i][k]+moder)%moder;
				ans+=tong[b[k]]++;
			}
			for(int k=1;k<=m;k++) tong[b[k]]=0;
		}
	printf("%lld\n",ans);
	return 0;
}

矩阵+前缀和思路：

发现题目中的单调性

当问“倍数”时，考虑取膜，与前缀和结合计数

另外敲敲说一句 看到入阵曲/星空/将军令这三首歌题的时候激动了一下==！