POJ 3321 Apple Tree 树状数组+DFS

题意：一棵苹果树有n个结点，编号从1到n，根结点永远是1。该树有n-1条树枝，每条树枝连接两个结点。已知苹果只会结在树的结点处，而且每个结点最多只能结1个苹果。初始时每个结点处都有1个苹果。树的主人接下来会进行m个操作。操作共两种。C X表示将结点x上的苹果数量改变，原本是1，则现在为0，原本是0，现在是1。Q X表示一次查询。要求输出结点X和其子树上的苹果总数。n和m最大可到100000。

操作只有更新和查询两种，树状数组最合适了。

首先是树状数组的相关知识。网上有很多讲解，在这里传送一个讲解的地址 传送门

树状数组最重要的就是要搞明白那种经典的图，之后就没什么问题了。

思路：本题的关键是如何将树映射成线性的数组。而且树状数组一般是对连续区间求和，又依照题意的要求，树的子树要在区间内也是连续存储的。这里的方法是，采用dfs对树进行一次遍历，树的每一个结点都有st和ed两个时间戳，分别记录该结点被遍历到的时间戳以及它和它的子树全部遍历完后的时间戳。举一个例子来说明。

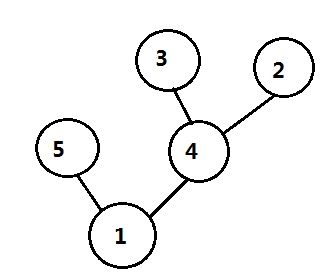
依次遍历到的结点：1  5  4  3  2

对应的时间戳：1  2  3  4  5

拿结点4来说，它的开始时间戳st为3，结束时间戳ed为5。

这样的话，假如需要询问结点x和它子树上的苹果总数，只需对区间[st[x], ed[x]]求和即可。另外需要注意的是，树状数组求和函数query求的是区间[1, x]的和，因此要实现之前的求和，需要用query(ed[x]) - query(st[x] - 1)。 （query(0) = 0）

以上就是解题思路了。

此外要注意，在建图的时候，添加边应该是双向边（即无向边），不然在遍历时会出现遍历不到或者其他问题。一开始我提交了两次总是tle，问题就在这里。

至于树状数组更新的时候，假设更新位置为x，则应将后续的x += lowbit[x]的位置也更新，直到x大于n。做这题时，我以为只要更新到结点x的结束位置ed[x]即可，但基于树状数组的特点，x变化后，后续结点即使不在x的子树里也是有可能受影响的，应当更新。不然在求和时就会得出错误结果。

 #include<stdio.h>
 #include<string.h>
 #define maxn 100020
 #define maxp 200020
 struct node
 {
     int v;
     int next;
 }edge[maxp];
 int num_edge, head[maxn];
 void addedge(int a, int b)
 {
     edge[num_edge].v = b;
     edge[num_edge].next = head[a];
     head[a] = num_edge++;
 }
 void init_edge()
 {
     num_edge=;
     memset(head,-,sizeof(head));
 }

 int st[maxn], ed[maxn], vis[maxn], cnt;//cnt记录时间戳，初始为0
 void get_timestamp(int u)
 {
     vis[u] = ;
     st[u] = ++cnt;//记录开始时间戳
     for (int i = head[u]; i != -; i = edge[i].next)
     {
         int v = edge[i].v;
         if (!vis[v]) get_timestamp(v);
     }
     ed[u] = cnt;//记录结束时间戳
 }

 int lowbit[maxn], apple[maxn];
 int n;//fork的总数
 void update(int x,int num)
 {
     for (int i = x; i <= n; i += lowbit[i])
         apple[i] += num;
 }
 int query(int x)
 {
     int res = ;
     for (int i = x; i > ; i -= lowbit[i])
         res += apple[i];
     return res;
 }
 int main()
 {
     //freopen("data.in", "r", stdin);
     scanf("%d",&n);
     init_edge();
     for (int i = ; i < n; i++)
     {
         int u, v;
         scanf("%d%d",&u,&v);
         addedge(u, v);
         addedge(v, u);
     }
     cnt = ;
     memset(vis, , sizeof(vis));
     get_timestamp();
     for (int i = ; i <= n; i++)
         lowbit[i] = i & (i ^ (i - ));
     for (int i = ; i <= n; i++)
         update(i, );
     int m;
     scanf("%d",&m);
     while (m--)
     {
         char op;
         int x;
         getchar();
         scanf("%c %d",&op,&x);
         if (op == 'Q')
             printf("%d\n",query(ed[x]) - query(st[x] - ));
         else
         {
             if (query(st[x]) - query(st[x] - ) == )
                 update(st[x], -);
             else update(st[x], );
         }
     }
     return ;
 }