lfyzoj104 Counting Swaps

问题描述

给定你一个 \(1 \sim n\) 的排列 \(\{p_i\}\)，可进行若干次操作，每次选择两个整数 \(x,y\)，交换 \(p_x,p_y\)。

请你告诉穰子，用最少的操作次数将给定排列变成单调上升的序列 \(1,2,\ldots,n\)，有多少种方式呢？请输出方式数对 \(10^9+9\) 取模的结果。

输入格式

第一行一个整数 \(T\) 代表数据组数。

每一组测试数据，第一行是一个整数 \(n\) 代表排列中的元素个数，第二行 \(n\) 个整数，是这个排列。

输入数据中测试数据间也许存在空行，请务必注意。

输出格式

\(T\) 行，一行一个整数，代表这组测试数据的答案。

样例一

input

1
3
2 3 1

output

3

explanation

至少需要两步，有三种操作方式。

• 先换 \(2,3\)，再换 \(3,1\)。
• 先换 \(2,1\)，再换 \(3,2\)。
• 先换 \(3,1\)，再换 \(2,1\)。

数据范围与约定

对于 \(50\%\) 的数据，\(1 \leq n \leq 10\)。

对于 \(100\%\) 的数据，\(1 \leq n \leq 100000\)，\(T=100\)。

时间限制： \(1\mathrm{s}\)

内存限制： \(256\mathrm{MB}\)

来源

ipsc2016c

---

题解

对于每个点 \(i\)，将他和他的身上的权值 \(p_i\) 代表的那个点连边。最后构成了许多许多的长度 \(\in [1,n]\) 的环。

把长度为 \(n\) 的环变成 \(n\) 个长度为 \(1\) 的自环，最少需要 \(n-1\) 次操作。这可以用数学归纳法证明。

记 \(F_n\) 为把长度为 \(n\) 的环变成 \(n\) 个长度为 \(1\) 的自环，在步数最小的前提下的操作方式数。

要想把长度为 \(n\) 的环变成 \(n\) 个长度为 \(1\) 的自环，首先肯定要将它划分成长度为 \(x,y\) 且 \(x+y=n\) 的两个环。

那么，有多少种划分方式呢？我们记把长度为 \(n\) 的环划分成长度为 \(x,y\) 且 \(x+y=n\) 的两个环的方式数为 \(T(x,y)\)。 我们考虑这样一个图：

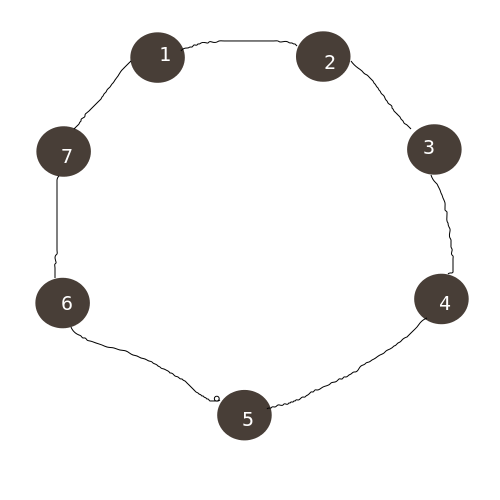
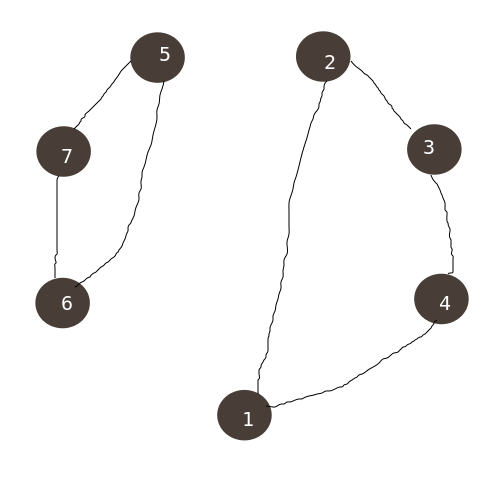
这个是交换了 \(1,5\)。你也可以交换 \(2,5\)。

我们发现，对于每个点，总有两个合适的点来和这个点交换，以达到划分的目的。因此，\(T(x,y)\) 为 \(2n/2=n\)。

但是，我们发现，当 \(n\) 为偶数且 \(x=y\) 时，这两个点会重合， \(T(x,y)\) 变成 \(n/2\)。

所以，

\[T(x,y)=\begin{cases}
n/2, & n \equiv 0 \pmod 2\ \mathrm{and}\ x=y\\
n, & \mathrm{others}
\end{cases}
\]

我们再考虑一下操作次序的问题。显然地，两个环之间互不影响。可以把一个环看成一类，用可重集排列数计算 \(x-1\) 步和 \(y-1\) 步之间怎么“交错”。“交错”的方法数依据公式，也就是 \((n-2)!/((x-1)!(y-1)!)\)。

因此，根据可重集排列数、加法原理、乘法原理，我们得到

\[F_n=\sum_{x+y=n} T(x,y)F_xF_y\dfrac{(n-2)!}{(x-1)!(y-1)!}
\]

用 dfs 找出所有的环，它们的长度为 \(l_1,l_2,\ldots,l_k\)，则再考虑考虑“交错”的方法数，我们得到答案

\[\prod_{i=1}^{k}F_{l_i} \times \dfrac{(n-k)!}{\prod_{i=1}^k(l_i-1)!}
\]

阶乘肯定与模数 \(10^9+9\) 互素，因此用费马小定理求逆元即可。

这样的时间复杂度是 \(\mathrm{O}(n^2)\)。

俗话说打表是第一生产力。我们在研究 \(F_i\) 的规律时，意外地发现 \(F_i=i^{i-2}\)。（我也不会证明……如果您会证明，请联系我）。这样，时间复杂度变为 \(\mathrm{O}(n \log n)\)。

当然，如果你信不过这个规律，你也可以打一个 \(F_i\) 的表放到代码里头……这样的时间复杂度是 \(\mathrm{O}(\mathrm{It\ would\ be\ accepted})\)……

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long ll;
int n, uu, hea[100005], cnt, bel[100005], din, hav[100005], ans, T;
int jie[100005];
struct Edge{
	int too, nxt;
}edge[200005];
const int mod=1e9+9;
void add_edge(int fro, int too){
	edge[++cnt].nxt = hea[fro];
	edge[cnt].too = too;
	hea[fro] = cnt;
}
void dfs(int x, int c){
	bel[x] = c;
	for(int i=hea[x]; i; i=edge[i].nxt){
		int t=edge[i].too;
		if(!bel[t])
			dfs(t, c);
	}
}
int ksm(int a, int b){
	if(!a)	return 1;
	if(b<0)	return 1;
	int re=1;
	while(b){
		if(b&1)	re = ((ll)re * a) % mod;
		a = ((ll)a * a) % mod;
		b >>= 1;
	}
	return re;
}
int main(){
	cin>>T;
	jie[0] = 1;
	for(int i=1; i<=100000; i++)
		jie[i] = ((ll)jie[i-1] * i) % mod;
	while(T--){
		memset(hav, 0, sizeof(hav));
		memset(bel, 0, sizeof(bel));
		memset(hea, 0, sizeof(hea));
		cnt = din = 0;
		scanf("%d", &n);
		for(int i=1; i<=n; i++){
			scanf("%d", &uu);
			add_edge(i, uu);
			add_edge(uu, i);
		}
		for(int i=1; i<=n; i++)
			if(!bel[i])
				dfs(i, ++din);
		for(int i=1; i<=n; i++)
			hav[bel[i]]++;
		ans = 1;
		for(int i=1; i<=din; i++)
			ans = ((ll)ans * ksm(hav[i], hav[i]-2)) % mod;
		ans = ((ll)ans * jie[n-din]) % mod;
		for(int i=1; i<=din; i++)
			ans = ((ll)ans * ksm(jie[hav[i]-1], mod-2)) % mod;
		cout<<ans<<endl;
	}
	return 0;
}