CF1706E Qpwoeirut and Vertices 题解

题目链接：CF 或者 洛谷

官解看上去挺智慧的，来点朴素的解法。我们来当做纯 ds 题去做。首先明确一点，图中若干个点关于最早连通性的这个问题可以考虑 \(MST\)，我们有一类东西叫 \(kruskal\) 重构树。这玩意其实只需要记住它的性质和建树方式即可，证明其实也是比较简单的，基于 \(kruskal\) 的构造 \(MST\) 过程反证法即可。

先说说这棵树有啥性质：

原图中两个点间所有路径上的边最大权值的最小值 \(=\) 最小生成树上两点简单路径的边最大权值 \(=\ Kruskal\) 重构树上两点 \(LCA\) 的点权。其实这玩意和笛卡尔树差不多，将 \(RMQ\) 问题变为树上的 \(LCA\) 问题。证明方式就因为你是按边权的从小到大去 \(merge\) 的，比较好证明出 \(MST\) 是具有以上性质的。

建树方式：

在 \(MST\) 的建造过程中，如果有两个点可以连通，我们就构造一个新的点，通常为 \(n+x\) 作为新点编号，然后作为它俩的 \(LCA\)，并为这个点赋予点权，其中点权为原来的边权，说直白点就是化边为点。并且此时，还需要将它们对应并查集的 \(fa\) 指向新点，同时建边。

回到本题

本题它有啥用，注意到本题每个边其实也是有边权的，边权其实为边的编号，最终问的是 \([l,r]\) 上的所有点连通时，\(1 \sim id\) 编号的边是已经加入了的，\(id\) 为满足的最小编号的边。先考虑一个简单情形：\(i\) 与 \(i+1\) 连通时加入的边即为它们的 \(LCA\)。这是为啥？在 \(kruskal\) 上每个新点其实就是代表着一条边，如果这两个点之间有边，显然就是 \(LCA\)，没有的话，显然等价于它们所在的连通分量的代表元连通之时，而它们的代表元联通以后形成的新点即为 \(LCA\)：

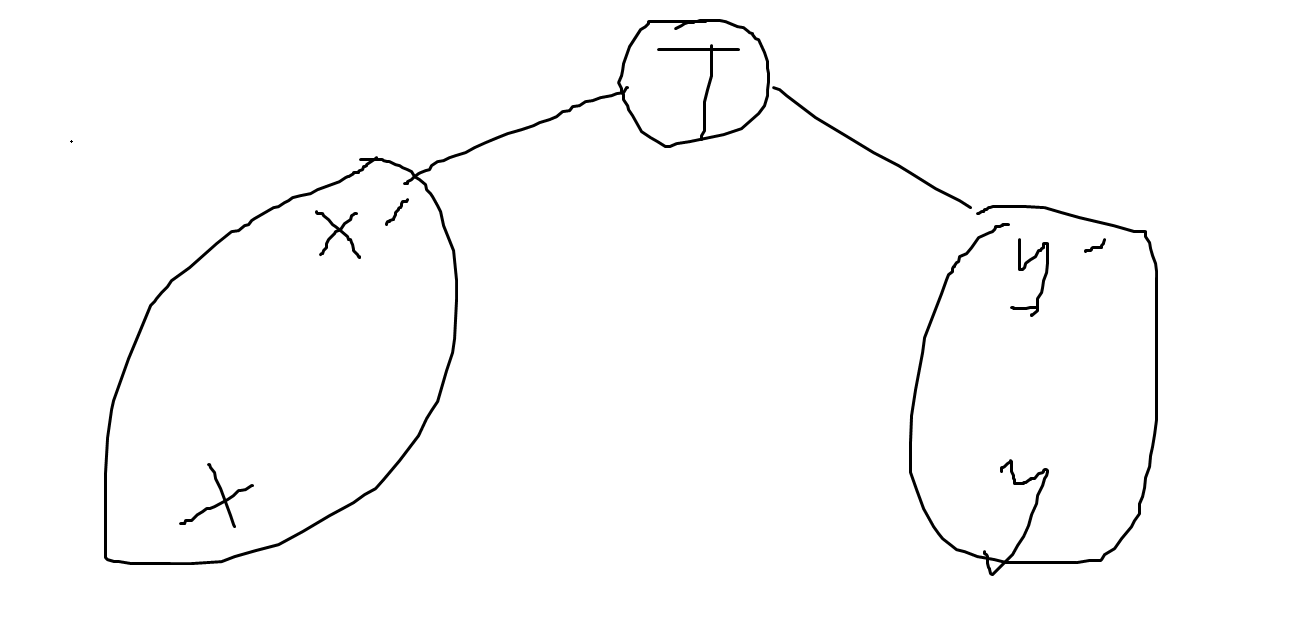
容易看出 \(x\) 和 \(y\) 连通的时间即为 \(x'\) 与 \(y'\) 之间的连边成为 \(T\) 这个点时也即为 \(x\) 和 \(y\) 的 \(LCA\)。

那么知道两个点的最早连通时间了，即为 \(LCA\) 的点权，因为本题里点权即为边的编号，如果是一堆点连通的最早时呢？显而易见是它们所有的 \(LCA\) 的点权。求一大堆点的 \(lca\) 怎么做：参考文章。其实就是这一堆点的 \(dfn\) 序最大和最小的两个点的 \(LCA\)。至此问题就全部解决了。

最终算法框架

首先边权即为边的编号，而编号显然由小到大输入，所以我们不需要排序了，对此建立 \(kruskal\) 重构树。然后跑 \(dfs\) 得到 \(dfn\) 序以及 \(lca\) 的倍增数组。然后由于需要查询区间上最大和最小的 \(dfn\) 序为多少，然后再拿到点，所以这个 \(RMQ\) 问题我们直接两个 \(ST\) 表就能解决。最后查询这两个点的 \(LCA\) 的点权即为所求的最早边的编号。当然注意多测清空和初始化问题。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

// #define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 5e5 + 10;
int n, m, q;
vector<int> kruskal[N]; //kruskal重构树
int val[N];

struct
{
    int tot;
    int fa[N];

    void init()
    {
        forn(i, 1, tot)kruskal[i].clear(), val[i] = 0;
        forn(i, 1, n<<1)fa[i] = i;
        tot = n;
    }

    int find(const int x)
    {
        return x == fa[x] ? x : fa[x] = find(fa[x]);
    }

    void merge(int x, int y, const int id)
    {
        x = find(x), y = find(y);
        if (x != y)
        {
            val[++tot] = id;
            fa[x] = fa[y] = tot;
            kruskal[tot].push_back(x), kruskal[tot].push_back(y);
            kruskal[x].push_back(tot), kruskal[y].push_back(tot);
        }
    }
} Kruskal;

constexpr int T = 25;
int cnt;
int fa[N][T + 1], dfn[N], rev[N], deep[N];

inline void dfs(const int curr, const int pa)
{
    dfn[curr] = ++cnt;
    rev[cnt] = curr;
    deep[curr] = deep[fa[curr][0] = pa] + 1;
    forn(i, 1, T)fa[curr][i] = fa[fa[curr][i - 1]][i - 1];
    for (const auto nxt : kruskal[curr])if (nxt != pa)dfs(nxt, curr);
}

inline int LCA(int x, int y)
{
    if (deep[x] < deep[y])swap(x, y);
    forv(i, T, 0)if (deep[fa[x][i]] >= deep[y])x = fa[x][i];
    if (x == y)return x;
    forv(i, T, 0)if (fa[x][i] != fa[y][i])x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}

//查询[1,n]上最大和最小的dfn序
int stMax[N][T], stMin[N][T];

inline void init()
{
    int k = log2(n) + 1;
    forn(i, 1, n)stMax[i][0] = stMin[i][0] = dfn[i];
    forn(j, 1, k)
    {
        forn(i, 1, n-(1<<j)+1)
        {
            stMax[i][j] = max(stMax[i][j - 1], stMax[i + (1 << j - 1)][j - 1]);
            stMin[i][j] = min(stMin[i][j - 1], stMin[i + (1 << j - 1)][j - 1]);
        }
    }
}

inline int query(const int l, const int r, const bool isMax = false)
{
    const int k = log2(r - l + 1);
    return isMax ? max(stMax[l][k], stMax[r - (1 << k) + 1][k]) : min(stMin[l][k], stMin[r - (1 << k) + 1][k]);
}

inline void clear()
{
    forn(i, 1, cnt)dfn[i] = rev[i] = 0;
    cnt = 0;
}

inline void solve()
{
    cin >> n >> m >> q;
    Kruskal.init();
    forn(i, 1, m)
    {
        int u, v;
        cin >> u >> v;
        Kruskal.merge(u, v, i);
    }
    clear();
    dfs(Kruskal.tot, 0); //遍历krusal重构树
    init(); //初始化ST表
    forn(i, 1, q)
    {
        int l, r;
        cin >> l >> r;
        if (l == r)cout << 0 << ' ';
        else
        {
            const int L = rev[query(l, r)], R = rev[query(l, r, true)]; //rev[dfn[i]]=i
            cout << val[LCA(L, R)] << ' '; //点权即为边的编号
        }
    }
    cout << endl;
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[
时间复杂度为:\ O((n+q)\log{n})
\]

当然，如果涉及到动态 \(MST\) 问题，我们用 \(LCT\) 去维护这棵重构树即可，原理一致。