数据结构图文解析之：二叉堆详解及C++模板实现

0. 数据结构图文解析系列

数据结构系列文章

数据结构图文解析之：数组、单链表、双链表介绍及C++模板实现

数据结构图文解析之：栈的简介及C++模板实现

数据结构图文解析之：队列详解与C++模板实现

数据结构图文解析之：树的简介及二叉排序树C++模板实现.

数据结构图文解析之：AVL树详解及C++模板实现

数据结构图文解析之：二叉堆详解及C++模板实现

1. 二叉堆的定义

二叉堆是一种特殊的堆，二叉堆是完全二叉树或近似完全二叉树。二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。

当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。

2. 二叉堆的存储

二叉堆一般使用数组来表示。请回忆一下二叉树的性质，其中有一条性质：

性质五：如果对一棵有n个节点的完全二叉树的节点按层序编号（从第一层开始到最下一层，每一层从左到右编号，从1开始编号），对任一节点i有：

1. 如果i=1 ，则节点为根节点，没有双亲。
2. 如果2 * i > n ，则节点i没有左孩子 ；否则其左孩子节点为2*i . （n为节点总数）
3. 如果2 * i+1>n ，则节点i没有右孩子；否则其右孩子节点为2*1+1.

简单来说：

1. 如果根节点在数组中的位置是1，第n个位置的子节点分别在2n 与 2n+1，第n个位置的双亲节点分别在⌊i /2⌋。因此，第1个位置的子节点在2和3.
2. 如果根节点在数组中的位置是0，第n个位置的子节点分别在2n+1与2n+2，第n个位置的双亲节点分别在⌊（i-1） /2⌋。因此，第0个位置的子节点在1和2.

得益于数组的随机存储能力，我们能够很快确定堆中节点的父节点与子节点。

下面以大顶堆展示一下堆的数组存储。

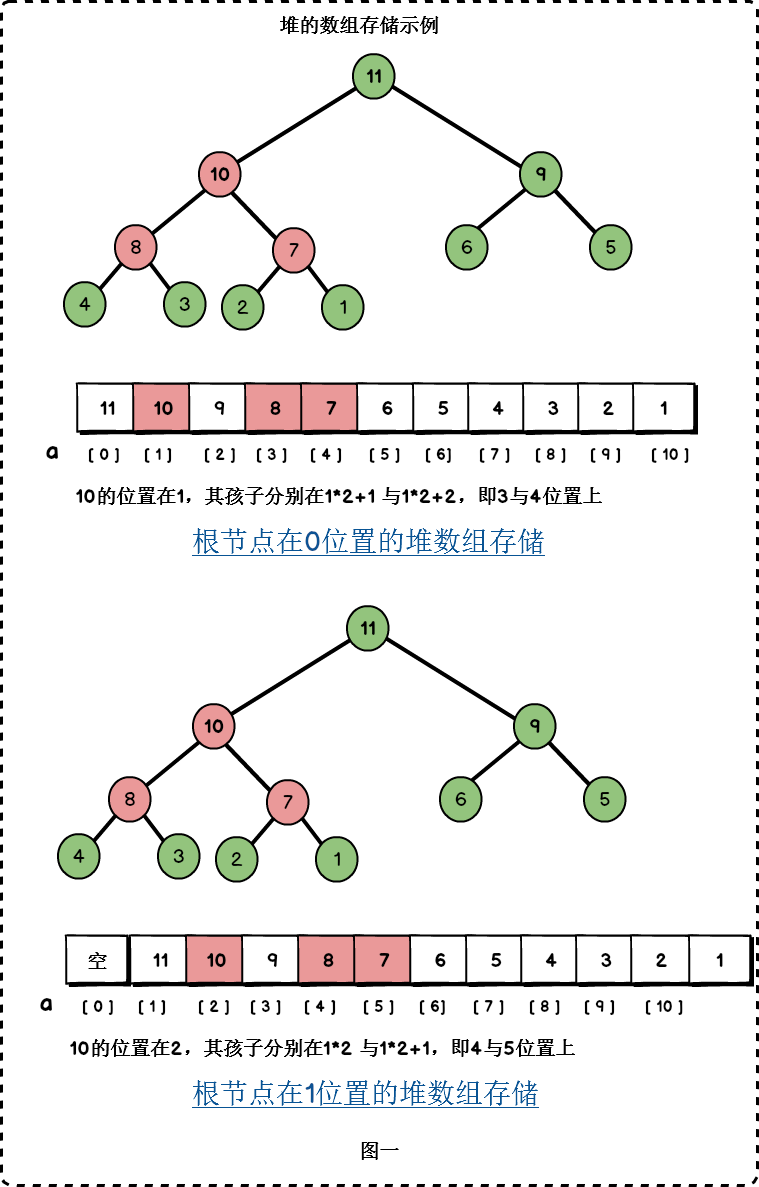
在本文中，我们以大顶堆为例进行堆的讲解。本文大顶堆的根节点位置为0.

3. 二叉堆的具体实现

在二叉堆上可以进行插入节点、删除节点、取出堆顶元素等操作。

3.1 二叉堆的抽象数据类型

/*大顶堆类定义*/
template <typename T>
class MaxHeap
{
public:
	bool insert(T val);		//往二叉堆中插入元素
	bool remove(T data);	//移除元素
	void print();			//打印堆
	T getTop();				//获取堆顶元素
	bool createMaxHeap(T a[], int size);//根据指定的数组来创建一个最大堆

	MaxHeap(int cap = 10);
	~MaxHeap();

private:
	int capacity;	//容量，也即是数组的大小
	int size;		//堆大小，也即是数组中有效元素的个数
	T * heap;		//底层的数组
private:
	void filterUp(int index); //从index所在节点，往根节点调整堆
	void filterDown(int begin ,int end ); //从begin所在节点开始，向end方向调整堆
};

1. 注意capacity与size的区别。capacity指的是数组的固有大小。size值数组中有效元素的个数，有效元素为组成堆的元素。
2. heap为数组。

3.2 二叉堆的插入

在数组的最末尾插入新节点，然后自下而上地调整子节点与父节点的位置：比较当前结点与父节点的大小，若不满足大顶堆的性质，则交换两节点，从而使当前子树满足二叉堆的性质。时间复杂度为O(logn)。

当我们在上图的堆中插入元素12：

调整过程：

1. 节点12添加在数组尾部，位置为11；
2. 节点12的双亲位置为⌊11/2⌋ = 5，即节点6；节点12比节点6大，与节点6交换位置。交换后节点12的位置为5.
3. 节点12的双亲位置为⌊ 5 /2⌋ = 2,即节点9；节点12比节点9大，与节点9交换位置。交换后节点12的位置为2.
4. 节点12的双亲位置为⌊2/2⌋ = 1，即节点11；节点12比节点11大，与节点11交换位置。交换后节点12的位置为1.
5. 12已经到达根节点，调整过程结束。

这个从下到上的调整过程为：

/*从下到上调整堆*/
/*插入元素时候使用*/
template <typename T>
void MaxHeap<T>::filterUp(int index)
{
	T value = heap[index];	//插入节点的值，图中的12

	while (index > 0) //如果还未到达根节点，继续调整
	{
		int indexParent = (index -1)/ 2;  //求其双亲节点
		if (value< heap[indexParent])
			break;
		else
		{
			heap[index] = heap[indexParent];
			index = indexParent;
		}
	}
	heap[index] = value;	//12插入最后的位置
};

在真正编程的时候，为了效率我们不必进行节点的交换，直接用父节点的值覆盖子节点。最后把新节点插入它最后的位置即可。

基于这个调整函数，我们的插入函数为：

/*插入元素*/
template <typename T>
bool MaxHeap<T>::insert(T val)
{
    if (size == capacity) //如果数组已满，则返回false
        return false;
    heap[size] = val;
    filterUp(size);
    size++;
    return true;
};

3.3 二叉堆的删除

堆的删除是这样一个过程：用数组最末尾节点覆盖被删节点，再从该节点从上到下调整二叉堆。我们删除根节点12：

可能有人疑惑，删除后数组最末尾不是多了一个6吗？

的确，但我们把数组中有效元素的个数减少了一，最末尾的6并不是堆的组成元素。

这个从上到下的调整过程为：

/*从上到下调整堆*/
/*删除元素时候使用*/
template<typename T>
void MaxHeap<T>::filterDown(int current,int end)
{

	int child = current * 2 + 1; //当前结点的左孩子

	T value = heap[current];	//保存当前结点的值

	while (child <= end)
	{
		if (child < end && heap[child] < heap[child+1])//选出两个孩子中较大的孩子
			child++;
		if (value>heap[child])	//无须调整；调整结束
			break;
		else
		{
			heap[current] = heap[child];	//孩子节点覆盖当前结点
			current = child;				//向下移动
			child = child * 2 + 1;
		}
	}
	heap[current] = value;
};

基于调整函数的删除函数：

/*删除元素*/
template<typename T>
bool MaxHeap<T>::remove(T data)
{
    if (size == 0) //如果堆是空的
        return false;
    int index;
    for (index = 0; index < size; index++)  //获取值在数组中的索引
    {
        if (heap[index] == data)
            break;
    }
    if (index == size)            //数组中没有该值
        return false; 

    heap[index] = heap[size - 1]; //使用最后一个节点来代替当前结点，然后再向下调整当前结点。

    filterDown(index,size--);  

    return true;
};

3.4 其余操作

其余操作很简单，不在这里啰嗦。

/*打印大顶堆*/
template <typename T>
void MaxHeap<T>::print()
{
    for (int i = 0; i < size; i++)
        cout << heap[i] << " ";
};
/*获取堆顶元素*/
template <typename T>
T MaxHeap<T>::getTop()
{
    if (size != 0)
        return heap[0];
};

/*根据指定的数组来创建一个最大堆*/
template<typename T>
bool MaxHeap<T>::createMapHeap(T a[], int size)
{
	if (size > capacity)	//	堆的容量不足以创建
		return false;
	for (int i = 0; i < size; i++)
	{
		insert(a[i]);
	}
	return true;
};

4. 二叉堆代码测试

测试代码：

int _tmain(int argc, _TCHAR* argv[])
{
	MaxHeap<int> heap(11);
	//逐个元素构建大顶堆
	for (int i = 0; i < 10; i++)
	{
		heap.insert(i);
	}
	heap.print();
	cout << endl;
	heap.remove(8);
	heap.print();
	cout << endl;

	//根据指定的数组创建大顶堆
	MaxHeap<int> heap2(11);
	int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
	heap2.createMaxHeap(a, 10);
	heap2.print();
	getchar();
	return 0;
}

运行结果：

9 8 5 6 7 1 4 0 3 2
9 7 5 6 2 1 4 0 3
10 9 6 7 8 2 5 1 4 3

5. 大顶堆、小顶堆完整代码下载

二叉堆完整代码：https://github.com/huanzheWu/Data-Structure/blob/master/MaxHeap/MaxHeap/MaxHeap.h

小顶堆完整代码：https://github.com/huanzheWu/Data-Structure/blob/master/MinHeap/MinHeap/MinHeap.h

原创文章，转载请注明出处：http://www.cnblogs.com/QG-whz/p/5173112.html