【Python】【demo实验10】【练习实例】【打印斐波那契数列】

斐波那契数列介绍：

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

与黄金分割关系

有趣的是，这样一个完全是自然数的数列，通项公式却是用无理数来表达的。而且当n趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割0.618（或者说后一项与前一项的比值小数部分越来越逼近0.618）。

1÷1=1，1÷2=0.5，2÷3=0.666...，3÷5=0.6，5÷8=0.625…………，55÷89=0.617977……………144÷233=0.618025…46368÷75025=0.6180339886…...

越到后面，这些比值越接近黄金比.

 

 我的源代码：

#!/usr/bin/python
# encoding=utf-8
# -*- coding: UTF-8 -*-
 
# 斐波那契数列
# 打印斐波那契数列
l = []
l.append(1)
l.append(1)
for i in range(2,300):
    l.append(l[i-1]+l[i-2])
    print(l)

结果：

原题给出的几种实现方法：

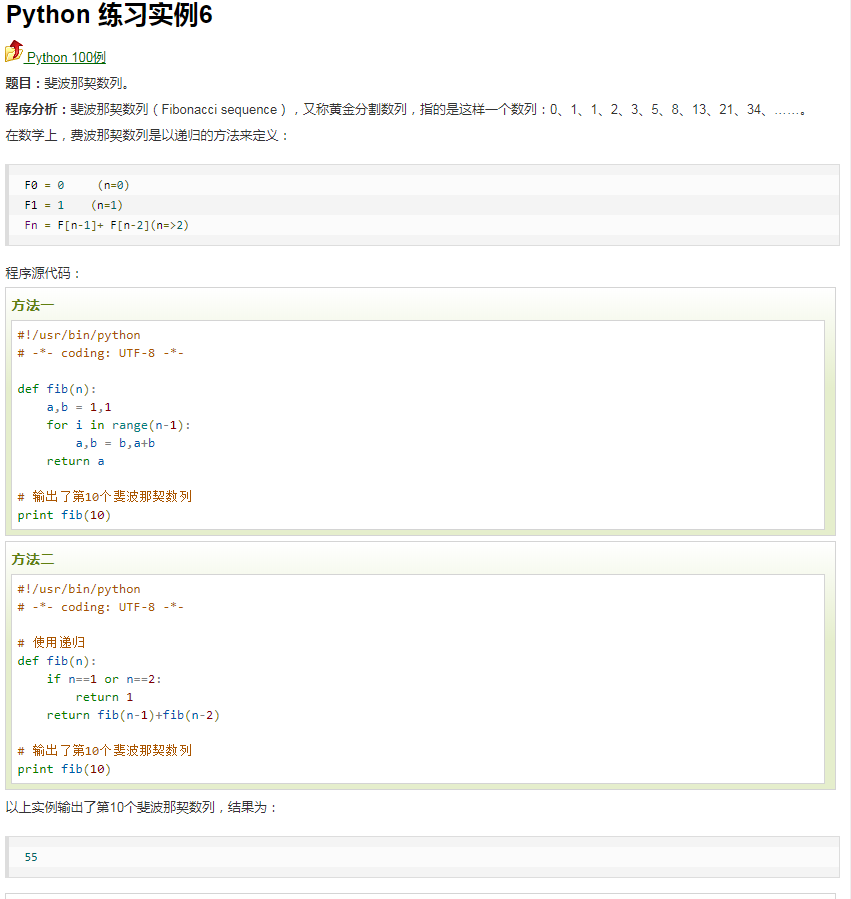
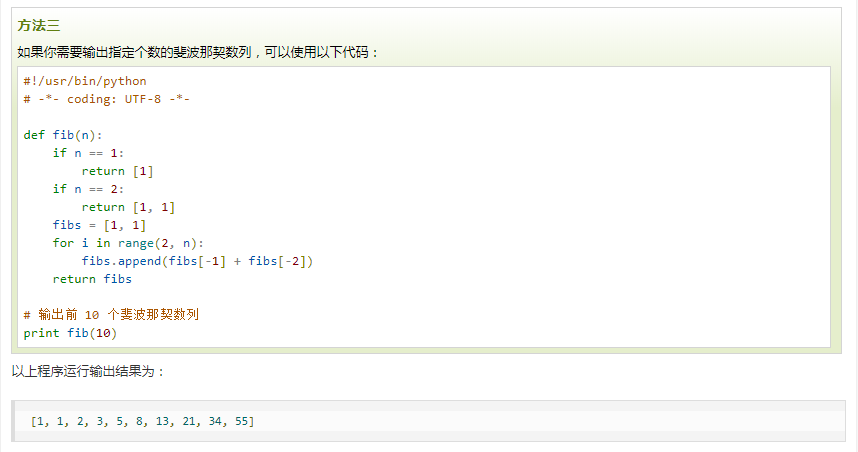
————————（我是分割线）————————

参考：

1. RUNOOB.COM  ： https://www.runoob.com/python/python-exercise-example6.html

2. 百度百科：https://baike.baidu.com/item/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97/99145?fr=aladdin

备注：

初次编辑时间：2019年9月24日12:16:20

环境：Windows 7   / Python 3.7.2