洛谷P4047 [JSOI2010]部落划分题解

题目描述

聪聪研究发现，荒岛野人总是过着群居的生活，但是，并不是整个荒岛上的所有野人都属于同一个部落，野人们总是拉帮结派形成属于自己的部落，不同的部落之间则经常发生争斗。只是，这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。

不过好消息是，聪聪得到了一份荒岛的地图。地图上标注了N个野人居住的地点（可以看作是平面上的坐标）。我们知道，同一个部落的野人总是生活在附近。我们把两个部落的距离，定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了K个部落！这真是个好消息。聪聪希望从这些信息里挖掘出所有部落的详细信息。他正在尝试这样一种算法：

对于任意一种部落划分的方法，都能够求出两个部落之间的距离，聪聪希望求出一种部落划分的方法，使靠得最近的两个部落尽可能远离。

例如，下面的左图表示了一个好的划分，而右图则不是。请你编程帮助聪聪解决这个难题。

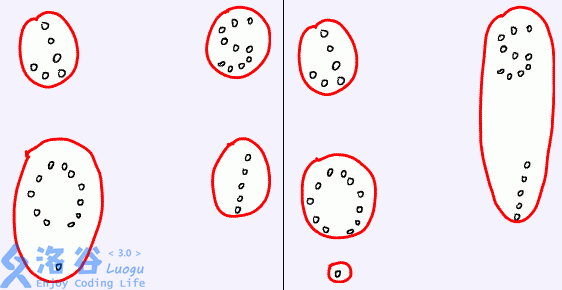
输入输出格式

输入格式：

输入文件第一行包含两个整数N和K(1<=N<=1000,1<K<=N)，分别代表了野人居住点的数量和部落的数量。

接下来N行，每行包含两个正整数x,y，描述了一个居住点的坐标(0<=x, y<=10000)。

输出格式：

输出一行，为最优划分时，最近的两个部落的距离，精确到小数点后两位。

输入输出样例

输入样例#1：

输出样例#1：

1.00

输入样例#2：

输出样例#2：

2.00

解析：

输入所有的点的坐标,然后就枚举记录每一个点到另外其他点的距离,注意要用double类型.
然后就排一个序,我这里是用结构体重载运算符,先从最小的开始合并并查集,并把这个边设为一个极大值,注意要把其他的点也要合并,就是说for循环一遍把所有在一个部落里的点与点之间的距离也设为一个极大值.
最后就在所有的边中取一个最小值,该值即为所值.

 #include <cstdio>

 #include <iostream>

 #include <cstdlib>

 #include <queue>

 #include <cstring>

 #include <stack>

 #include <cmath>

 #include <algorithm>

 #include <iomanip>

 #include <ctime>

 #define INF 0x7fffffff

 #define Max 1000025

 inline int read()

 {

     int s=,f=;

     char ch=getchar();

     while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar();}

     while(ch>=''&&ch<='') s=s*+ch-'',ch=getchar();

     return s*f;

 }

 int n,k,pa[Max],x[Max],y[Max],ID[Max];

 int find(int x)

 {

     if(x!=pa[x])

         pa[x]=find(pa[x]);

     return pa[x];

 }

 void add(int x,int y)

 {

     x=find(x);y=find(y);

     pa[y]=x;

 }

 #define D double

 D d(int x_1,int y_1,int x_2,int y_2)

 {

     return (D)sqrt((x_1-x_2)*(x_1-x_2) + (y_1-y_2)*(y_1-y_2));

 }

 struct point

 {

     int x,y;

     D dis;

     friend bool operator<(point a,point b) {

         return a.dis<b.dis;

     }

 }t[Max];

 int main()

 {

 //    freopen("Group.in","r",stdin);

 //    freopen("Group.out","w",stdout);

     n=read();k=read();

     for(int i =  ; i <= n ; ++ i)

         pa[i]=i;

     for(int i =  ; i <= n ; ++ i)

         x[i]=read(),y[i]=read(),ID[i]=i;

     int num=;

     for(int i =  ; i <= n ; ++ i)

         for(int j =  ; j <= n ; ++ j)

             if(i!=j) {

                 t[++num].dis=d(x[i],y[i],x[j],y[j]);

                 t[num].x=ID[i];t[num].y=ID[j];

             }

     int m=n;

     D Min=INF;

     std::sort(t+,t++num);

     for(int i =  ; i <= num ; ++ i) {

         int x=find(t[i].x),y=find(t[i].y);

         if(x!=y)

             add(x,y),m--,t[i].dis=INF*1.00;

         if(m==k)

             break;

     }

     for(int i =  ; i <= num ; ++ i)

         if(find(t[i].x)==find(t[i].y))

             t[i].dis=INF*1.0;

     for(int i =  ; i <= num ; ++ i)

         Min=std::min(Min,t[i].dis);

     printf("%.2lf",Min);

     return ;

 }

AC代码